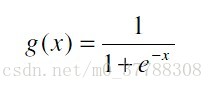本文主要是介绍卷积神经网络和TextCNN(原理+代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
卷积神经网络(Convolutional Neural Network, CNN)是一种前馈神经网络,它的人工神经元可以响应一部分覆盖范围内的周围单元,对于大型图像处理有出色表现。
##概况
卷积神经网络(Convolutional Neural Networks / CNNs / ConvNets)与普通神经网络非常相似,它们都由具有可学习的权重和偏置常量(biases)的神经元组成。每个神经元都接收一些输入,并做一些点积计算,输出是每个分类的分数(概率),普通神经网络里的一些计算技巧到这里依旧适用。
1、卷积神经网络(CNN)
所以哪里不同呢?
神经网络到卷积神经网络
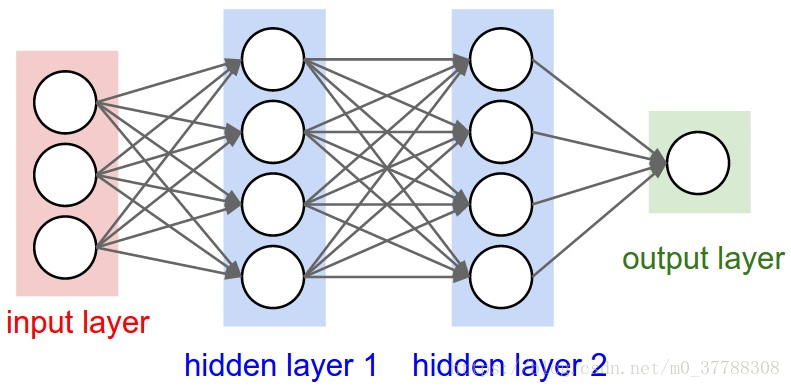
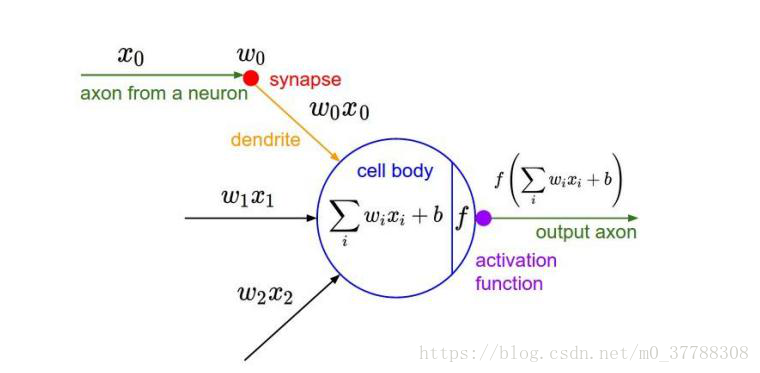
神经网络广义上的一般形式如下图,有输入层,输出层以及中间层。并且层与层之间的连线叫做权重(W),作为传递信号。
我们大概已经了解神经网络对于很多分类问题有了很好的结果,但是这是需要一个前提的,这个前提就是分类的类别相对较少。如果当你面临比较多的分类问题的时候,你还想用神经网络,那么就会出现两个问题:
(1)深的网络结构,更多的神经元,浪费资源
(2)过拟合
针对第一个问题,当你面临多分类的问题是,势必需要架起层次更深的神经网络,这就意味着需要更多的神经元。这里举一个例子,比如Alexnet神经网络,这是一个7层的神经网络,每一层的神经元个数达到4096,我们可以从上面的神经网络的一般形式看出,每两层之间(因为是全连接)的权重(W)就达到4096 X 4096,而这仅仅是两层之间,面对七层的神经网络,权重(W)的量级可想而知。所以如果支撑起这个Alexnet神经网络,就需要有足够的电脑资源,才能使得输入的数据做前项运算、后向传播、迭代、优化。
针对第二个问题,当神经网络的层次多起来的时候,它的学习能力非常强,也就是有非常强的记忆能力,以至于当你的数据没有达到一定的量级,它可以轻而易举的把你的训练集数据全部记下来,这是做机器学习都不愿遇到的问题,就是过拟合现象。直观的表现就是它可以在你的训练集上表现的非常好,但是在同等条件下,你输入其他的问题,它的回答就不那么好,就是泛化能力很差。
针对这两个问题,后来就发展了很多的神经网络,其中就包括比较常用的卷积神经网络。
卷积神经网络之层级结构
数据输入层 / input layer
包括三种比较常用的数据处理方式
1、去均值
把输入数据各个维度都中心化0
2、归一化
幅度归一化到同样的范围
3、PCA / 白化
用PCA降维(保证独立性)
白化是对数据每个特征轴上的幅度归一化
卷及计算层 / CONV layer
首先卷积层是卷积神经神经网络的灵魂,非常的重要。
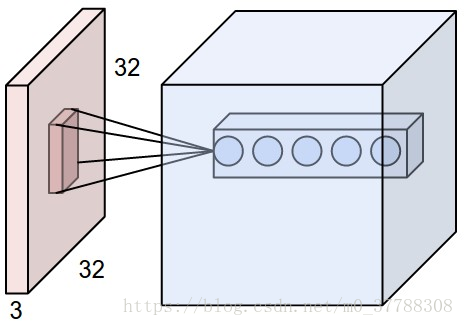
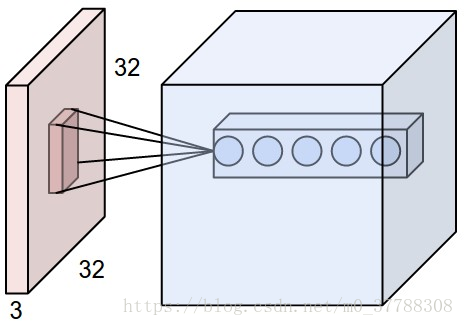
1、局部关联。每个神经元看做一个filter
2、窗口滑动,filter对局部数据计算
在对图像的认识,我们发现一个性质,叫局部关联性。比如一个图像的一个像素点,与之关系最大的是在其周围的像素点,也就是说把图像的主体截下来,它周边的东西也不会对主体造成很大的影响。
当我们对整个图像进行处理比较困难的时候,我们这时候采取一个办法,就是取一个数据窗口,它要做的事就是从图像的左上角依次滑到右下角,使得整个图像全部滑过一遍,这样就可以把整个图形的信息扫面下来。
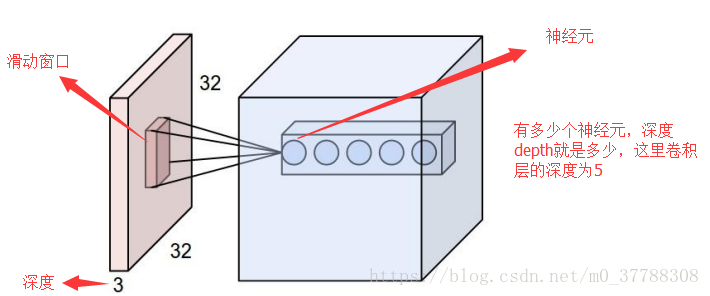
这里需要重点提及的是每层的神经元的功能都是不一样的,比如第一个神经元它在做窗口滑动的时候只提取其中一个特征,二下一个神经元只提取另一个特征,依次下去,最后把这些汇总起来(这和神经网络的区别是,神经网络的神经元是把图片的所有信息提取下来然后再汇总)。并且上面图形里面的神经元与窗口的连线表示权重(W)。
窗口滑动就需要提出三个概念
(1)深度(depth)
(2)步长(stride)
(3)填充值(zero-padding)
下面依次介绍这三个的意义:
深度可以直观的理解为下一层神经元的个数。比如上面图中的卷积层有五个神经元,那么这里卷积层的深度就是5
步长表示的是窗口每次滑动需要滑几步,人为设定的。步长的设定最好低于你的数据窗口的维数,这样可以更好地提取图形的信息
填充值是当我们设定的数据窗口在一定的步长上滑动时,无法滑动到下去而补充的值,一般为0
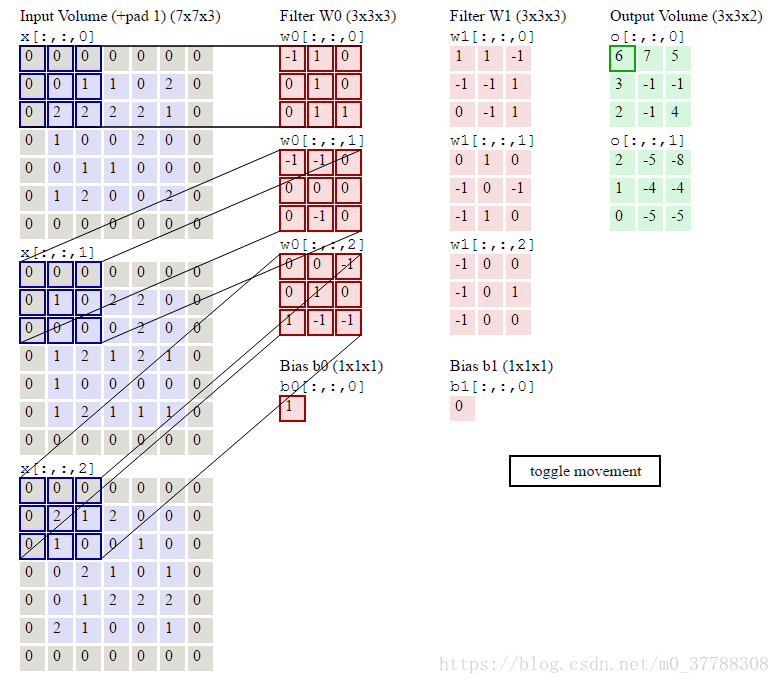
这个动图形象的介绍了神经元在提取图像特征时所做的内积的过程。Filter W0表示第一个神经元,Filter W1表示第二个神经元。其中W0下有三个矩阵是因为我们的输入对象是一个RGB彩色图片,它有三个颜色通道,需要对它们同时提取信息。
参数共享
我们直观的从图片上看,因为数据窗口每次都在滑动,并且面对的信息也不一样,自然而然的认为权重(W)一直在变。但是呢,卷积神经网络在这里做了一个设定,就是使这些W固定不变,也就是参数共享,目的就是减少参数,事实证明,进过机器的学习,并不会影响我们对图像的识别。
卷积层总结
1、固定每个神经元连接权重(参数共享),可以看做模板
2、每个神经元只关注一个特性
3、需要估算的权重个数减少:AlexNet 1亿 => 3.5万
4、一组固定的权重和不同窗口内数据做内积:卷积
这个图片直观的告诉大家,第一个神经元(filter)只提取一个特征(图片的形状),第二个图片也只提取一个特征(图像的纹理)。
激励层
我们从卷积层通过运算得到的一些结果,但是要判断这些结果要不要往下继续往下传,或者要以什么样的幅度往下传,这就需要把从卷积层的输出结果做非线性变换
这个图片说明了从卷积层得到的结果并不是直接往下传的,需要加入激励函数,下面介绍比较常见的几种激励函数
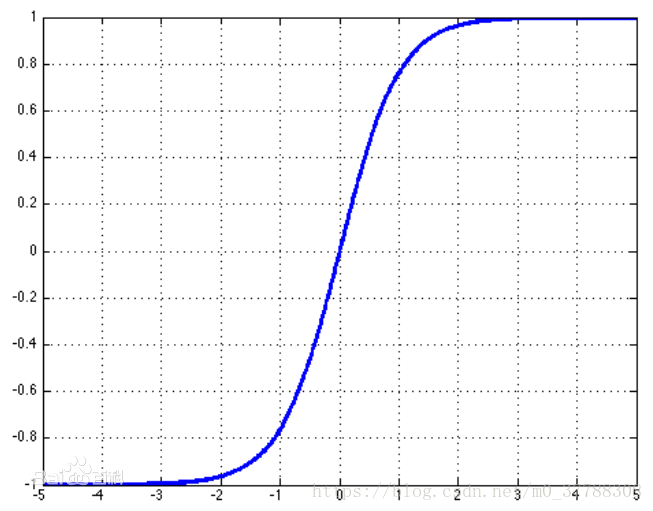
1、Sigmoid
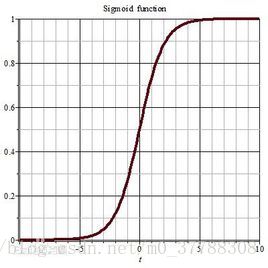
图形为:
sigmod激励函数符合实际,当输入很小时,输出接近于0;当输入很大时,输出值接近1。但sigmod函数存在较大的缺点:
1、当输入值很小时或很大时,输出曲线基本就是直线了,回想一下反向传播的过程,我们最后用于迭代的梯度,是由中间这些梯度值结果相乘得到的,因此如果中间的局部梯度值非常小,直接会把最终梯度结果拉近0,意味着存在梯度趋向为0
2、非零中心化,也就是当输入为0时,输出不为0,,因为每一层的输出都要作为下一层的输入,而未0中心化会直接影响梯度下降,我们这么举个例子吧,如果输出的结果均值不为0,举个极端的例子,全部为正的话(例如f=wTx+b中所有x>0),那么反向传播回传到w上的梯度将要么全部为正要么全部为负(取决于f的梯度正负性),这带来的后果是,反向传播得到的梯度用于权重更新的时候,不是平缓地迭代变化,而是类似锯齿状的突变。影响梯度下降的动态性
2、Tanh(双曲正切)
图像为:
与sigmoid相比,输出至的范围变成了0中心化[-1, 1]。但梯度消失现象依然存在。所以在实际应用中,tanh激励函数还是比sigmoid要用的多一些的
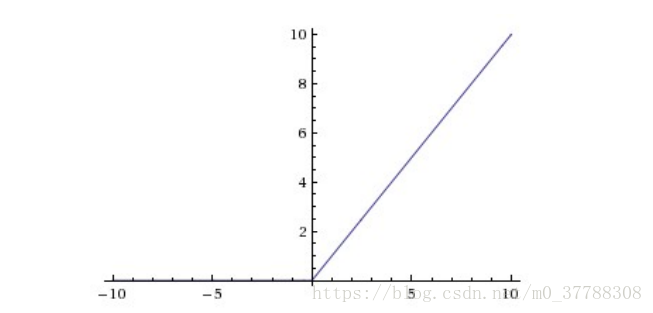
#### ReLU(the Rectified Linear Unit / 修正线性单元)
函数的基本形式为: f ( x ) = m a x ( 0 , x ) f\left ( x \right )=max\left ( 0,x \right ) f(x)=max(0,x)
图像为:
优点:
(1)不会出现梯度消失,收敛速度快;
(2)前向计算量小,只需要计算max(0, x),不像sigmoid中有指数计算;
(3)反向传播计算快,导数计算简单,无需指数、出发计算;
(4)有些神经元的值为0,使网络具有saprse性质,可减小过拟合。
缺点:
比较脆弱,在训练时容易“die”,反向传播中如果一个参数为0,后面的参数就会不更新。使用合适的学习当然,这和参数设置有关系,所以我们要特别小心,举个实际的例子哈,如果学习速率被设的太高,结果你会发现,训练的过程中可能有高达40%的ReLU单元都挂掉了。所以我们要小心设定初始的学习率等参数,在一定程度上控制这个问题。率会减弱这种情况。
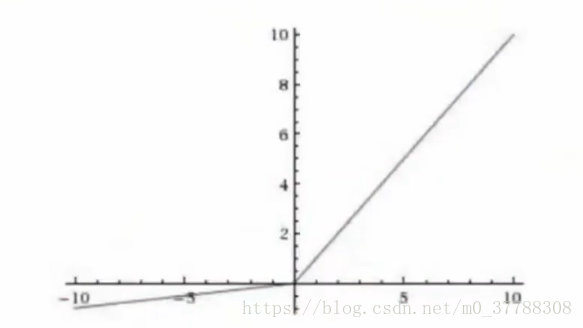
3、Leaky ReLU
函数为: f ( x ) = { x x > 0 0.01 x o t h e r s f\left ( x \right )=\left\{\begin{matrix} x & x>0& \\ 0.01x& others& \end{matrix}\right. f(x)={x0.01xx>0others
图像为:
优点:ReLU有的全都有,并且不会die,是ReLU的改进
缺点:计算量略大,效果不会很稳定
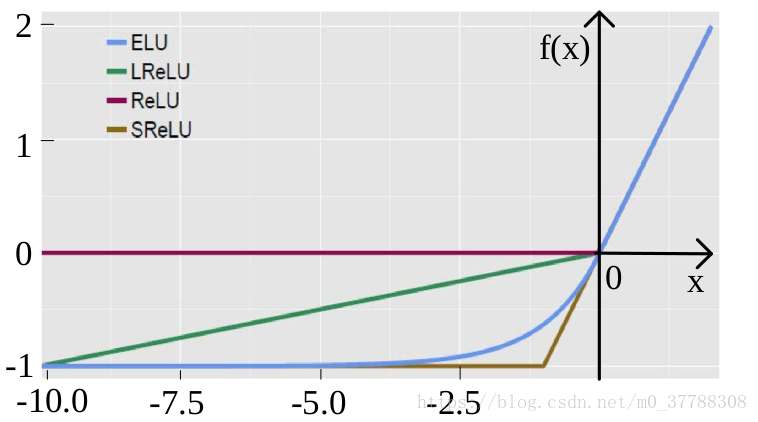
4、指数线性单元ELU
函数为: f ( x ) = { x x > 0 α ( e x p ( x ) − 1 ) o t h e r s f\left ( x \right )=\left\{\begin{matrix} x & x>0& \\ \alpha \left ( exp\left ( x \right ) -1\right )& others& \end{matrix}\right. f(x)={xα(exp(x)−1)x>0others
图像为:
优点:所有ReLU的优点都有,不会挂,输出均值趋于0
缺点:因为指数存在,计算量略大
5、Maxout
函数为: f ( x ) = m a x ( w 1 T + b 1 , w 2 T + b 2 ) f\left ( x \right )=max\left ( w_{1}^{T}+b_{1}, w_{2}^{T}+b_{2}\right ) f(x)=max(w1T+b1,w2T+b2)
优点:Maxout函数是对ReLU和Leaky ReLU的一般化归纳,这样就拥有了ReLU的所有优点(线性和不饱和),而没有它的缺点
缺点:它每个神经元的参数数量增加一倍,这就导致了整体参数的数量激增
6、激励层(实际经验)
不要用sigmoid!不要用sigmoid!不要用sigmoid!
首先试RELU,因为快,但要小心点
如果2失效,请用Leaky ReLU或者Maxout
某些情况下tanh倒是有不错的结果,但是很少
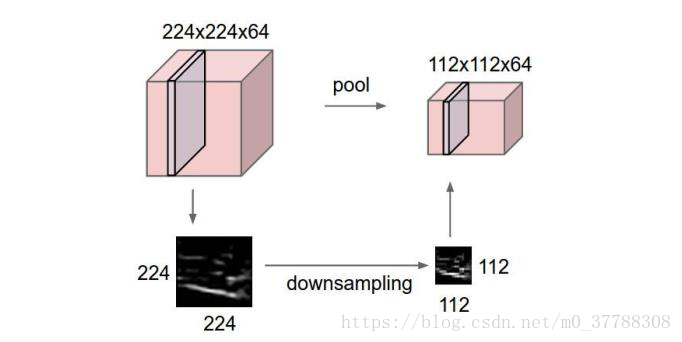
池化层
夹在连续的卷积层中间
进行下采样,压缩数据和参数的量,减少过拟合
不需要引入新权重
我们对图片有个直观的认识,就是将图片放小任然可以认出这是个什么图片内容,所以池化层就利用这一点进一步压缩数据,减少参数的数量,减少过拟合。
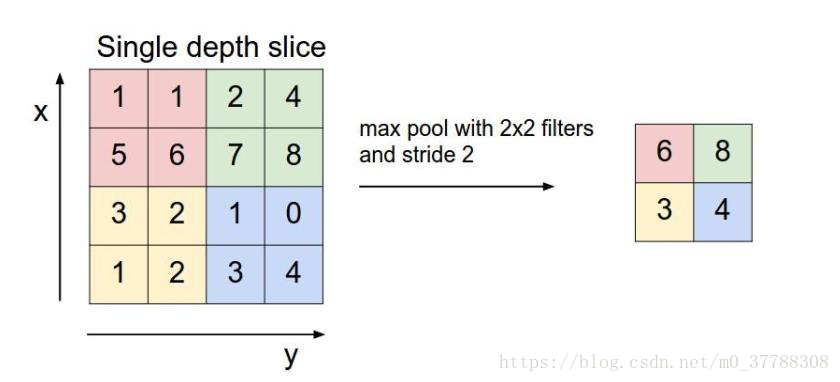
这里介绍两个常用的方法Max pooling 和average pooling,以Max pooling为例
从图中很明显就可以看出来它是取每个区域的最大值,来得到新的结果,并且参数从25降到了9。所以即达到了图像识别的效果,又使得参数得到了减少,为什么不用呢???
全连接层(Fully-connected layer)
全连接层和卷积层可以相互转换:
* 对于任意一个卷积层,要把它变成全连接层只需要把权重变成一个巨大的矩阵,其中大部分都是0 除了一些特定区块(因为局部感知),而且好多区块的权值还相同(由于权重共享)。
* 相反地,对于任何一个全连接层也可以变为卷积层。比如,一个K=4096K=4096 的全连接层,输入层大小为 7∗7∗5127∗7∗512,它可以等效为一个 F=7, P=0, S=1, K=4096F=7, P=0, S=1, K=4096 的卷积层。换言之,我们把 filter size 正好设置为整个输入层大小。
一般CNN结构依次为
INPUT
[[CONV -> RELU]*N -> POOL?]*M
[FC -> RELU]*K
FC
问号表示pooling层可有可无,这取决于你的数据量有多大,取决你的当前问题的数据量级支持它不会那么快的过拟合。
训练算法
同一般机器学习算法,先定义Loss function,衡量与实际结果之间差距
找到最小化损失函数的W和b,CNN中的算法是SGD
SGD需要计算W和b的偏导
BP算法就是计算偏导用的
BP算法的核心是求导链式法则
总结下来就是:
BP算法利用链式求导法则,逐级相乘直到求解出dw和db
利用SGD/随机梯度下降,迭代和更新W和b
优缺点
优点
共享卷积核,对高维数据处理无压力
无需手动选取特征,训练好权重,即得特征
分类效果好
缺点
需要调参,需要大样本量,训练最好要GPU
物理含义不明确
CNN在图像处理层面受到了广泛的应用,也收到了很好的效果,日前CNN网络在图像层面发展迅速,基于更高的硬件需求,CNN表现出更好的效果,本问在上文原理的介绍下,对CNN在文本处理领域的运用做一些简单的介绍。
2、TextCnn
原文下载
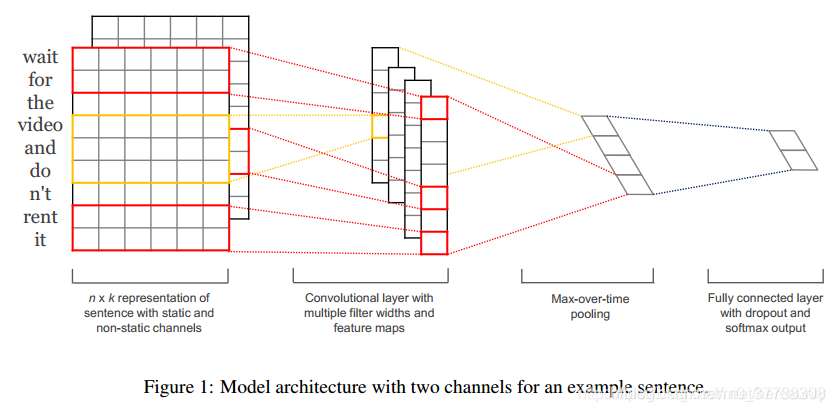
可以发现textCNN的结构与CNN结构一直。
2.1 词嵌入
首先句子可以看作是词的序列,序列长度为n,每个词用向量 x i x_{i} xi表示,每个词嵌入的维度是k。所以句子表示为: x i : n = x 1 ⊕ x 2 ⊕ : : : ⊕ x n x_{i:n} = x_{1}\oplus x_{2}\oplus :::\oplus x_{n} xi:n=x1⊕x2⊕:::⊕xn所 x i : i + j x_{i:i+j} xi:i+j是个左闭右闭的区间。
2.2 卷积
由于不同的论文对卷积的表达是不同的,所以以上图为例。上图中宽代表词向量,高代表不同的词。
由于TextCNN采用的卷积是一维卷积,所以卷积核的宽度和词嵌入的维度是一致的。而卷积核的高度h代表的是每次窗口取的词数。所以卷积核 ω ∈ R h k \omega \in \mathbb{R}^{hk} ω∈Rhk。
对于每一次滑窗的结果 c i c_{i} ci(标量)而言,卷积运算的结果是
c i = f ( ω ⋅ x i : i + h − 1 ) + b c_{i}=f\left ( \omega \cdot x_{i:i+h-1} \right )+b ci=f(ω⋅xi:i+h−1)+b其中 b ∈ R b\in \mathbb{R} b∈R,而f是非线性函数,例如tanh或者relu。
由于卷积运算是对应元素相乘然后相加,所以 ω \omega ω和 x i : i + h − 1 x_{i:i+h-1} xi:i+h−1的维度是一致的。由于 ω \omega ω的维度是 h ∗ k h*k h∗k, x i : i + h − 1 x_{i:i+h-1} xi:i+h−1的维度也是 h ∗ k h*k h∗k,则X的维度是 ( n − h + 1 ) ∗ h ∗ k \left ( n-h+1 \right )*h*k (n−h+1)∗h∗k(和c的维度可以对照得到)。
由于句子序列长度为n,而卷积核的高度为h,所以总共滑窗n−h+1次。所以卷积汇总结果为 c = [ c 1 , c 2 , . . . , c n − h + 1 ] c=\left [ c_{1},c_{2},...,c_{n-h+1} \right ] c=[c1,c2,...,cn−h+1]
2.3 池化
这里的池化采用的是全局最大池化,即 c ^ = m a x { c } \hat{c}=max\left \{ c \right \} c^=max{c}。由于filter一般有多个,假设卷积核个数是m,所以池化后的数据为 z = [ c 1 ^ , c 2 ^ , . . . , c m ^ ] z=\left [ \hat{c_{1}},\hat{c_{2}},...,\hat{c_{m}} \right ] z=[c1^,c2^,...,cm^]数据维度为1∗m (列向量)。
2.4 DNN+softmax
y = ω ∗ z + b y=\omega * z + b y=ω∗z+b
这篇关于卷积神经网络和TextCNN(原理+代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!