本文主要是介绍语音分帧加窗,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
预加重
语音信号的预加重,目的是为了对语音的高频部分进行加重,去除口唇辐射的影响,增加语音的高频分辨率。一般通过传递函数为一阶FIR高通数字滤波器来实现预加重,其中a为预加重系数,0.9<a<1.0。设n时刻的语音采样值为x(n),经过预加重处理后的结果为y(n))=x(n)-ax(n-1),这里取a=0.98。
简单理解就是在频域上面都乘以一个系数,这个系数跟频率成正相关,所以高频的幅值会有所提升。
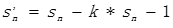
分帧(chunk)
傅里叶变换要求输入的信号的平稳的。

语音信号在宏观上是不平稳的,在微观上是平稳的,具有短时平稳性(10—30ms内可以认为语音信号近似不变),这个就可以把语音信号分为一些短段来进行处理,每一个短段称为一帧(CHUNK)。
如果后续操作需要加窗,则在分帧的时候,不要背靠背地截取,而是相互重叠一部分。相邻两帧的起始位置的时间差叫做帧移(STRIDE)。
加窗

在数字处理时必须把长时间的信号序列截断。如图2.35中,x(t)为一余弦信号,其频谱是X(f),它是位于±f0处的d函数。矩形窗函数w(t)的频谱是W(f) ,它是一个sinc(f)函数。当用一个w(t)去截断x(t)时,得到截断后的信号为x(t)*w(t),根据傅立叶变换关系,其频谱为X(f)*W(f)。

x(t)被截断后的频谱不同于它加窗以前的频谱。由于w(t)是一个频带无限的函数,所以即使x(t)是带限信号,在截断以后也必然变成无限带宽的函数。原来集中在±f0处的能量被分散到以±f0为中心的两个较宽的频带上,也就是有一部分能量泄漏到x(t)的频带以外。为了减少泄漏应该尽量寻找频域中接近d(f)的窗函数W(f),即主瓣窄旁瓣小的窗函数。
加窗即与一个窗函数相乘,加窗之后是为了进行傅里叶展开.
使全局更加连续,避免出现吉布斯效应。
加窗时候,原本没有周期性的语音信号呈现出周期函数的部分特征。
加窗的代价是一帧信号的两端部分被削弱了,所以在分帧的时候,帧与帧之间需要有重叠。
语音信号中一般都是要加上汉明窗,因为加上汉明窗,只有中间的数据体现出来了,两边的数据信息丢失了,所以等会移窗的时候,只会移1/3或1/2窗,这样被前一帧或二帧丢失的数据又重新得到了体现。
傅里叶变换
对一帧信号做傅里叶变换得到的结果叫做频谱
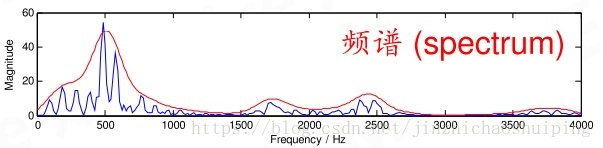
对语音信号处理主要的数学工具是傅里叶变换,而傅里叶变换是研究整个时间域和频率域的关系。不过,当运用计算机实现工程测试信号处理时,不可能对无限长的信号进行测量和运算,而是取其有限的时间片段进行分析。
这篇关于语音分帧加窗的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!