《初阶数据结构》尾声

本文主要是介绍《初阶数据结构》尾声，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言：

《快速排序（非递归）》:

《归并排序》：

《归并排序（非递归）》：

《计数排序》：

对于快速排序的优化：

分析：

总结：

前言：

上一篇blog重点讲解了《选择排序》《插入排序》，重点介绍了快速排序的三种方法，这篇blog主要讲解《归并排序》以及它的非递归使用方法，最后还会再补充一个计数排序。

上一篇的blog:《插入排序》与《选择排序》-CSDN博客

《快速排序（非递归）》:

typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort3(a, left, right);//分区间[left, keyi-1] keyi [keyi+1, right]if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}}STDestory(&s);
}

我们目前学习数据结构到此，由于我们呢接触了不少的递归操作，不难发现，其实递归的算法与栈这个数据结构较为类似。

我们还是一样先对整体进行排序，分别将begin和end入栈，然后设置好left和right。在第一次对总体排完序后，还是一如既往的会分出两个区间，我们又需要分别对左右两个区间进行排序。

在我们利用栈执行代码的时候要注意先后顺序，先入栈的后后访问，后入栈的先访问。

《归并排序》：

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end){return;}int mid = (end + begin) / 2;//[begin, mid] [mid + 1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);int begin1 = begin;int end1 = mid;int begin2 = mid + 1;int end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2])//<=才是稳定的{tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int)* (end - begin + 1));}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)* n);if (tmp == NULL){perror("tmp -> malloc");exit(-1);}_MergeSort(a, 0, n - 1, tmp);}

所谓归并，就是分而治之。

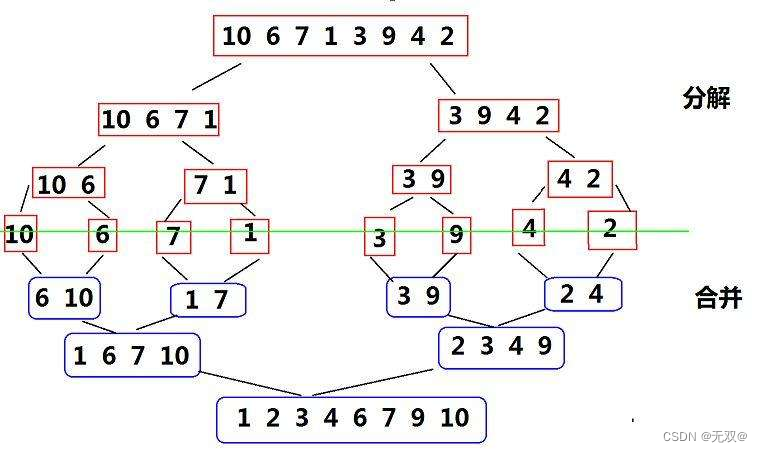
我们使用递归来实现数组的分割和合并，它的逻辑非常像二叉树的后序遍历，由于我们要使用递归，又要申请临时空间，所以我们先申请好临时空间，再将归并排序过程作为子函数调用，这样不用在每次递归过程申请释放空间

《归并排序（非递归）》：

我们在快速排序的非递归中运用了栈这一数据结构，而我们在实现归并排序中，不可以去使用栈这一数据结构。

首先我们要知道，如果我们不用栈，我们可以用哪些方法替代，一个我们熟知的方法，是栈，还有一个则是循环。

那么话说回来，为什么不能用栈呢？

对于归并排序来说，与我们在二叉树所介绍的后序遍历较为相似，属于是“先把每条路走了，再回来说再见”。相比较于快速排序，利用栈是先对总体进行排序，再分区间进行排序。

而归并排序呢，一上来就把左区间给排完了，那右区间该怎么找呢？出栈后还要在归并的过程中再次使用出栈后的子区间。

所以我们需要利用循环来进行处理。

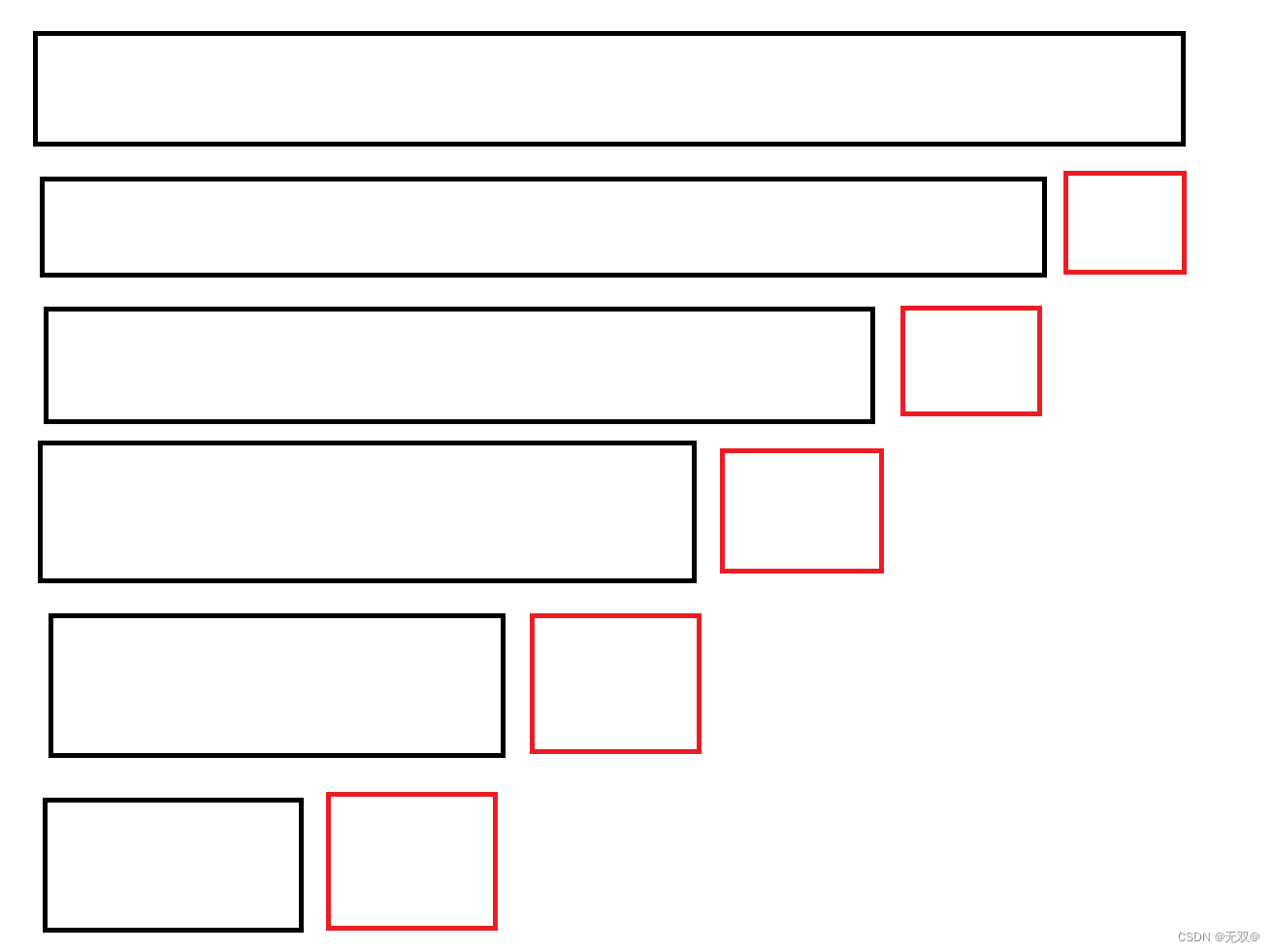
我们可以理解我从底层向上拓展，所以我们一开始是1个数据和1个数据进行比较，就像：

我们可以设置一个gap，就像希尔排序那样，只不过这次我们需要利用这个gap来限制end和begin

我们初始化gap == 1，意思就是两两比较，a[0]与a[1]比较分出大小，a[1]与a[2]比较分出大小，最后当下标越界了的时候，我们就可以开始对四个四个之间进行比较，让gap*=2即可分好下一个小组。

void MergeSortNoR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)* n);if (tmp == NULL){perror("tmp -> malloc");exit(-1);}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;if (end1 >= n || begin1 >= n){break;}if (end2 >= n){end2 = n - 1;}int j = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int)* (end2 - i + 1));}gap *= 2;}}

《计数排序》：

计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。操作步骤：
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中

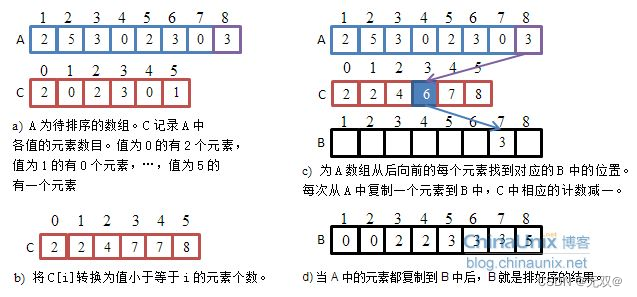
void CountSort(int* a, int n)
{int min = a[0];int max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;int* count = (int*)calloc(range, sizeof(int));//计数for (int i = 0; i < n; i++){count[a[i] - min]++;}//排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}}

这里我们做了一个优化，假设我们要排序2,3,8888,6666,诸如这样间隔相差很大的数字，如果不做优化处理就直接calloc新数组，那么会造成许多的空间浪费，所以减去最小值，减小空间的浪费。

这种排序的局限性集中于：

1.不适合分散的数据，适合集中的数据。

2.不适合浮点数、字符串、结构体数据排序，只适合整数。

对于快速排序的优化：

假设每次取的关键字key恰好是最大值或者最小值，即数组已经有序，这时的时间复杂度就是O(N^2)

所以我们可以找到最左边，最右边，和中间值，进行三数取中，谁不大不小就让谁做关键字并且与第一个数进行交换。

int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[midi] < a[begin]){if (a[end] < a[midi]){return midi;}else if (a[begin] < a[end]){return begin;}else{return end;}}else //a[midi]>a[begin]{if (a[end] > a[midi]){return midi;}else if (a[begin] > a[end]){return begin;}else{return begin;}}
}

分析：

我们可以通过随机生成100000个数来进行效率的测试。

//测试效率
void TestOp()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int)* N);int* a2 = (int*)malloc(sizeof(int)* N);int* a3 = (int*)malloc(sizeof(int)* N);int* a4 = (int*)malloc(sizeof(int)* N);int* a5 = (int*)malloc(sizeof(int)* N);int* a6 = (int*)malloc(sizeof(int)* N);int* a7 = (int*)malloc(sizeof(int)* N);int* a8 = (int*)malloc(sizeof(int)* N);int* a9 = (int*)malloc(sizeof(int)* N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a9[i] = a1[i];}for (int i = 0; i < N; i++){a8[i] = i;}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin9 = clock();CountSort(a9, N);int end9 = clock();printf("InsertSort(直接插入排序):%d\n", end1 - begin1);printf("ShellSort(希尔排序):%d\n", end2 - begin2);printf("SelectSort(选择排序):%d\n", end3 - begin3);printf("HeapSort(堆排序):%d\n", end4 - begin4);printf("QuickSort(快速排序):%d\n", end5 - begin5);printf("MergeSortSort(归并排序):%d\n", end6 - begin6);printf("CountSort(计数排序):%d\n", end9 - begin9);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);free(a9);
}