本文主要是介绍Normalization,LayerNormalization和BatchNormalization,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
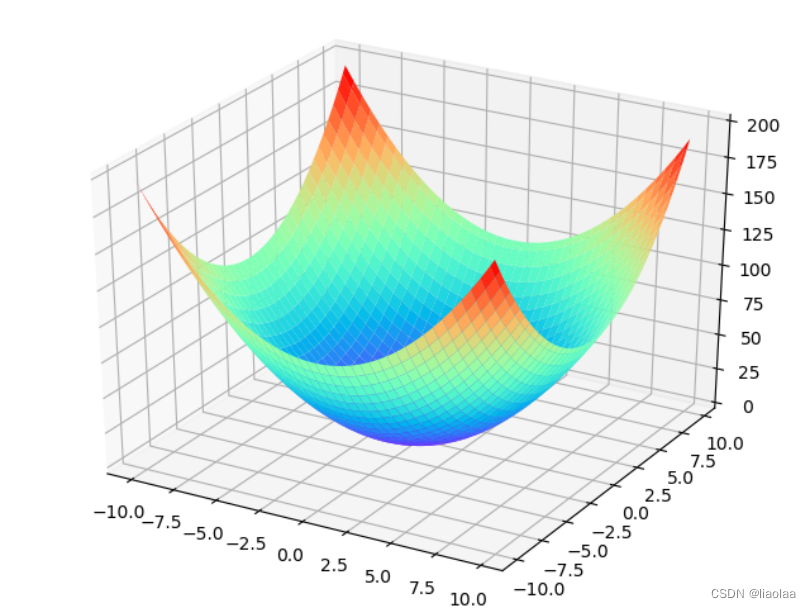
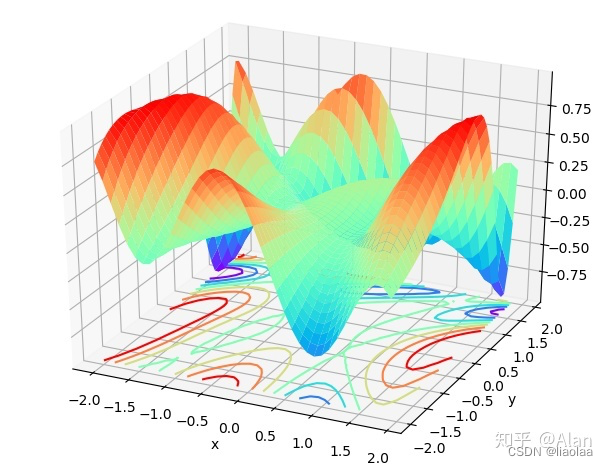
假设我们的损失函数在空间中是一个曲面,这个曲面可以被我们人为的切出等高线,在采用梯度下降算法的时候,我们沿着梯度反方向迭代(梯度方向与等高线垂直),到最后我们会抵达上图曲面的最低点。
在上面的两幅图中忽略坐标值,观察损失函数曲面在空间中的形状,把它们比作山坡,我们人在山顶,很明显左图下山的路一眼就能看清,右图下山的路需要边走边观察改变下山路线,一般的情况下左图是会比右图更快更容易到达山底的。
如下图所示,两个损失函数在空间的曲面的等高线(同一尺度的等高线),很明显可以看出左图的损失函数在空间中比较崎岖(可以参考上面右边那副图投影下来的等高线)而右图的损失函数在空间中比较平滑(可以参考上面左边那副图投影下来的等高线)。根据梯度下降算法,右图也就是等高线呈现正圆形时能够有最少的迭代步数,就可以抵达最低点,因此收敛速度更快。等高线是椭圆形的,会有更多的迭代步数才能到达函数最低点,收敛变慢。当然,这里面还存在着是不是最低点的问题,在这里先不考虑。
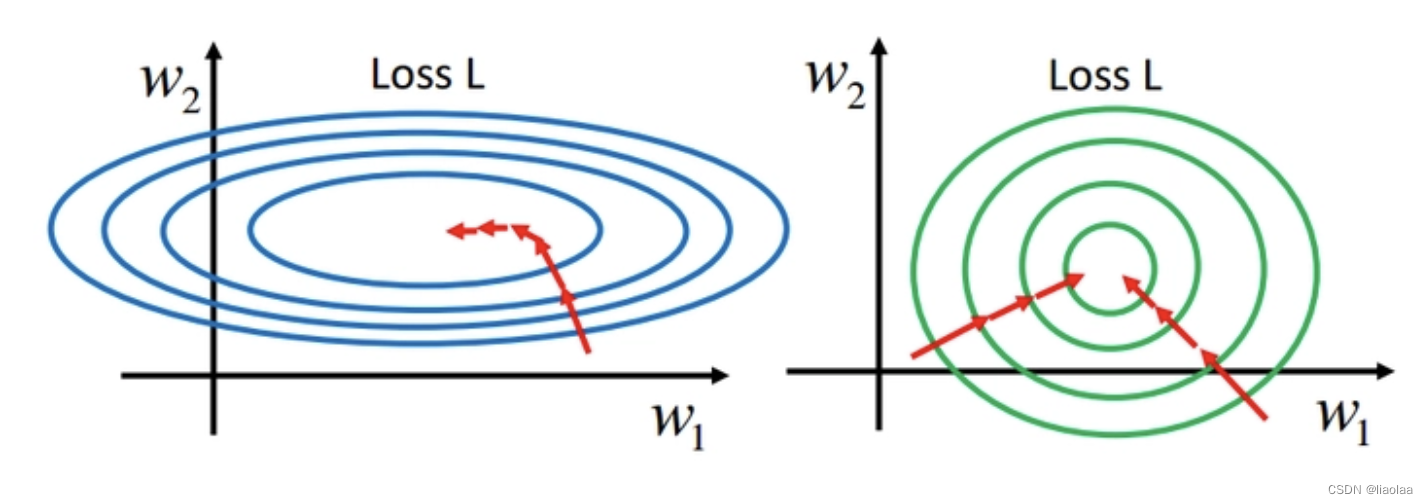
因此,我们知道我们的损失函数曲面应该要平滑不崎岖,即拥有正圆形的等高线。那么在什么样的情况下我们才能获得正圆形的等高线呢,又或者说是更接近正圆形的等高线呢?
为什么要做规范化?
我们有一个简单的线性回归模型 ,我们的输入特征是
和
,我们的损失函数根据
变化而变化。如果模型的输入
的范围远远小于
,在
和
相同变化时,
受到输入特征是
的影响会远小于
,进而损失函数受到输入特征是
的影响会远小于
,从而会产生椭圆形的损失函数曲面等高线。因此,在线性回归中若各个特征变量之间的取值范围差异较大,则会导致目标函数收敛速度慢等问题,需要对输入特征进行规范化,尽量避免形成椭圆形的等高线。
如果我们在上面的这个再加上一个激活函数,即 ,在激活函数接受到的值会对梯度存在很大的影响,会造成梯度消失的问题,因此,我们仍旧是需要做规范化,同时,规范化也有一定的抗过拟合作用,使训练过程更加平稳。
BN和LN

LN不考虑batch,它是对同一个feature同一个example里面不同的dimension之间做规范化;
BN需要考虑batch,它是对不同的feature不同的batch的同一个dimension之间做规范化。
所以BN抹平了不同特征之间的大小关系,而保留了不同样本之间的大小关系。这样,如果具体任务依赖于不同样本之间的关系,BN更有效,尤其是在CV领域,例如不同图片样本进行分类,不同样本之间的大小关系得以保留。
LN抹平了不同样本之间的大小关系,而保留了不同特征之间的大小关系。所以,LN更适合NLP领域的任务,其中,一个样本的特征实际上就是不同词嵌入维度,通过LN可以保留特征之间的这种时序关系。
并且在NLP任务中,每个样本之间的差异较大,序列是不定长的,长度不同的序列原则上属于不同的统计对象,所以很难得到稳定的统计量,而得不到稳定的统计量,具体可以参考 PowerNorm: Rethinking Batch Normalization in Transformers(https://arxiv.org/abs/2003.07845)
这篇关于Normalization,LayerNormalization和BatchNormalization的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!