Boosted Dynamic Neural Networks

本文主要是介绍Boosted Dynamic Neural Networks，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Boosted Dynamic Neural Networks

论文链接：https://arxiv.org/pdf/2211.16726.pdf
源码链接：https://github.com/SHI-Labs/Boosted-Dynamic-Networks

简介

尽管深度学习模型在各种计算机视觉任务上取得成功，但在实际应用中部署模型时，必须考虑计算资源的限制和推理效率。作为深度学习应用一个关键话题，高效深度学习最近得到了广泛的研究，包括高效架构设计，网络剪枝和网络量化。与对应的大baseline模型相比，这些轻量化模型通常表现出显著的推理加速，且性能下降很小或可以忽略不计。
动态神经网络是高效深度学习模型另一个分支。实际上轻量级模型运行速度更快，性能较低，而大模型运行速度较慢，性能较高。给定特定应用场景中计算资源预算，深度学习从业者通常需要在效率和性能之间找到适当的平衡点。然而，预算在许多情况下经常是动态变化的，例如，当计算资源大量被其他应用程序占用或边缘设备电池电量在一天内发生变化时。因此，在给定不同资源预算和性能要求的情况下，动态神经网络（DNN）可以在不同平衡点运行是可取的。
目前一堆各种动态方法进行了广泛的研究，包括动态模型架构、动态模型参数、动态空间感知推理等等。本文重点关注图像分类任务中早期存在的动态神经网络（EDNN），这是最广泛探索的动态架构方法之一。
EDNN的自适应推理属性来源于其可调整的层深度。在推理时，当计算预算紧张或输入示例容易识别时，EDNN在浅分类器处退出。相反，模型运行更多的层，直到最后一个分类器或给出可靠预测的分类器。为了训练这种EDNN模型，现有的方法通常对所有分类器进行联合优化。给定一批训练样本，模型将运行所有层和分类器并对损失进行累计和汇总。然后，总损失梯度反向传播到所有层。上述训练程序一个问题是训练-测试不匹配问题，该问题Dynamic neural networks: A survey中进行了讨论。在训练阶段，模型中所有分类器都会在所有训练样本上进行优化，而在推理阶段，并非所有分类器都能看到所有类型的测试数据。当计算资源紧张或输入容易处理时，只执行浅层与分类器。换句话说，在训练和测试阶段存在数据分布差距。尽管简单的例子也可能有助于在训练阶段对深度分类器进行正则化，但深度分类器设计不应过于关注于这些这些例子，以避免分布失配问题。
为了缓解训练-测试不匹配问题，本文提出了一种新的早退出动态网络，称为Boosted Dynamic Neural Network（BoostNet），其灵感来自著名的梯度提升（Gradient boosting）理论。假定最终模型是弱预测模型的加权和，梯度增强算法通过迭代最小化损失函数在函数空间中用梯度下降训练每个弱模型。在每个训练步骤中，选择指向损失函数负梯度的模型作为新的弱模型。将梯度增强纳入EDNN学习的一个简单方法是世界遵循传统方法梯度提升框架迭代训练分类器。然而这在实践中并不奏效。本文推测主要有两个原因。第一个原因是较深的分类器与较浅的分类器共享网络层，因此分类器在网络参数方面并不独立。第二个原因时多层神经网络不是弱预测模型。这两个特性不符合梯度增强的假设。因此，以梯度增强的方式简单地训练分类器是行不通的。
本文提出了BoostNet，它具有类似的梯度提升思想，但以适合动态神经网络的方式进行组织和训练。为了有效地训练模型，本文提出了三种训练技术。首先，对所有分类器进行联合优化。以梯度提升的方式训练弱分类器将导致整个模型的次优解。另一方面，在每个训练批上训练分类器是耗时的。因此，本文通过联合优化训练所有分类器。其次，本文提出了一种预测重加权策略，在使用当前分类器的集成成员之前重新缩放先前分类器集合。如果训练样本的训练损失足够大，将其定义为有效样本。本文实验表明，当网络进入更深的分类器时，有效训练数据的百分比会降低，为了避免深度分类器缺乏训练数据，使用温度来重新缩放先前分类器集合，以削弱其预测。第三，本文将梯度重新缩放技术应用于网络梯度，以约束不同层深度的参数梯度。

本文方法

总览

EDNN模型通常由多个子模型组成。在推理时，给定一个输入图像，本文运行模型直到第一个分类器的最后一层，以获得粗糙的预测。如果预测结果确信高于预定阈值，则可以尽在第一分类器处终止推理。否则，第二分类器将对来自第一分类器的特征执行。它有望给出更自信的预测，纠正第一个分类器所犯的错误。如果没有重复上述过程，直到某个分类器给出足够有信心的预测，或者达到最后一个分类器。为了训练模型，现有的EDNN方法在不考虑上述自适应推理特性的情况下联合训练所有分类器。考虑到N分类器的EDNN模型，总体任务损失为：
$L(x)=\sum_{n=1}^{N}w_{n}L_{n}(F_{n}(x),y)$
$F_{n}(x)$ 和 $w_{n}$ 是第n分类器预测和对总损失的贡献。这使得所有分类器以相同方式处理每个训练样本。然而，在推理时，模型将在容易输入的早期分类器处退出，因此深度分类器将尽在困难输入上执行。这种训练-测试不匹配问题将导致模型训练和测试阶段之间的数据分布差距，使训练后的模型变得次优。重新思考上述推断过程，本文发现EDNN模型的内在性质时，深层次的分类器通过纠正其错误来补充其先前的分类器。
首先简单介绍梯度提升理论。给定输入 $x$ 及其输出 $y$ ，梯度提升是找到一些函数 $F (x)$ 近似输出y。 $F$ 是多个基本分类器之和的形式：
$F(x)=\sum_{n=1}^{N}f_{n}(x)+C$
梯度增强按顺序优化每个弱分类器:
$\begin{aligned} F_{0}(x)&=\arg\min_{\alpha}L_{0}(\alpha,y)\\ F_{n}(x)&=F_{n-1}(x)+\arg\min_{f_{n}\in \mathcal{F}}L_{n}(F_{n-1}(x)+f_{n}(x),y)\\ \end{aligned}$
给定任意损失函数 $L_{n}$ 直接求解最优 $f_{n}$ 是困难的。梯度提升方法实现对上述的一阶估计：
$f_{n}(x)=\lambda \nabla_{F_{n-1}}L_{n}(F_{n-1}(x),y)$
受到梯度提升启发，本文将EDNN分类器组织成类似的结构。第n块最终输出是第n块及其所有先前块的输出的线性组合。与梯度提升中的一阶近似不同，本文通过多步的小批梯度下降直接优化神经网络 $f_{n}$ 的参数 $\theta_{n}$ 。
$\begin{aligned} \theta_{n}^{k}&=\theta_{n}^{k-1}-\lambda\nabla_{\theta}L_{n}(x;\theta_{n}^{k-1}) \\ \nabla_{\theta}L_{n}(x;\theta_{n}^{k-1})&=\nabla_{\theta}L_{n}(F_{n-1}(x)+f_{n}(x;\theta_{n}^{k-1}),y) \end{aligned}$
$F_{n-1}(x)$ 梯度被禁用，即使它与 $F_{n}$ 共享参数子集。

最小批联合优化

遵循传统的梯度提升方法，一个直接的优化过程是依次训练N个分类器，即训练分类器 $f_{n}$ 直到收敛，固定其分类头，然后训练 $f_{n+1}$ 。然而这使得所有比 $f_{n+1}$ 浅的分类器在训练 $f_{n+1}$ 时恶化，因为所有分类器分享相同的网络backbone。另一方面，固定共享参数之训练 $f_{n+1}$ 不共享部分将损害它表示能力。相反。本文采用了小批联合优化架构。给定一小批训练数据，传入整个BoostNet获得N个预测输出。然后，累加了N个输出上的训练损失，并进行一次反向传播。
$stop_grad ( F n − 1 ( x ) + f n ( x ) ) , y ) L(x)=\sum_{n=1}^{N}w_{n}L_{n}(\text{stop\_grad}(F_{n-1}(x)+f_{n}(x)),y)$

梯度重缩放

与Anytime Recognition with Routing Convolutional Networks类似，本文使用梯度重缩放操作重新缩放来自不同网络分支的梯度。本文在每个分支中乘以一个标量来重新缩放通过它的梯度。使用该操作，整体损失梯度 $L$ 描述为：
$\frac{\partial L}{\partial b_{n}}=\frac{1}{N-n+1}\sum_{i=n}^{N}\frac{\partial L_{i}}{\partial b_{n}}$
即使 $N$ 是一个很大的数字，它也是有界的，给出了一个较弱的假设 $\partial L_{i}/\partial b_{n}$ 是有界的。

基于温度的预测重缩放

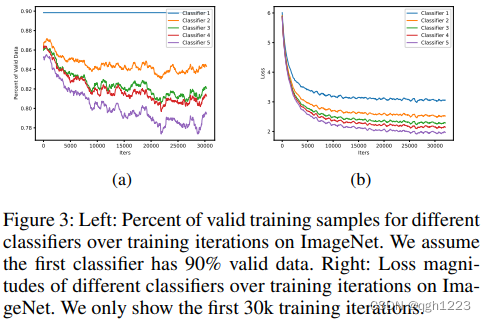
当在上述过程中进行训练时，观察到一个问题，即较深的分类器与较浅的分类器相比没有表现出太大的性能改进。当在上述过程中进行训练时，观察到一个问题，即较深的分类器与较浅的分类器相比没有表现出太大的性能提升，尽管模型大小增加了很大的幅度。图3a中显示每个分类器的训练样本数量。如果训练样本的训练损失大于某个阈值时，则训练样本是有效的。这里，将v设置为第一个分类器在每批训练数据中所有训练损失的第10个百分比，即假设第一个分类器总是具有90%的有效训练样本。图中发现较浅较浅的分类器具有更多有效的训练数据，而较深的分类器具有较少的训练数据。如图3b所示，本文展示了不同分类器的批平均训练损失。与图3a一致，较深的分类器具有较小的训练损失。从另一个角度来看，这可以通过以下事实解释，即更深的分类器具有更大的模型大小，从而具有更高的表示能力，但这也表明更深的分类器需要更具挑战性的训练样本，而不是学习较浅分类器的容易残差。为了解决这个问题，本文来作为 $F_{n}$ 的集成成员之前，将第n-1分类器的输出乘以温度 $t_{n}$ ：
$F_{n}=t_{n}F_{n-1}+f_{n}$
$F_{n-1},F_{n}$ 是softmax前预测logits。设置所有温度 ${t_{n}\}|_{n=1}^{N}$ 为0.5.本文将该技术称为预测重加权。这样浅分类器 $F_{n-1}$ 的集成输出相当于在基础输出中使用之前被削弱。
在这里插入图片描述