本文主要是介绍神经网络和逻辑电路——表面相同的设计形式,天壤之别的设计思想,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 神经网络与逻辑电路相似的表面形式
第一次看到神经网络这个理论的时候,首先呢,这个我脑子里边儿闪出的第一个念头就是它,它可能和我们传统的逻辑电路非常相似。
逻辑电路里边我们处理的数据,就是0、1两个数字.那么在神经网络里边呢,由于Sigmoid函数的存在,我们所处理的数据啊,是0到1之间的实数。所以从这个角度来讲的话,我想神经网络,它很可能是逻辑电路的一个推广,把0、1两个值推广到[0,1]这样一个区间上。
因此,从这个角度来看,神经网络里面的神经元,它所充当的角色就是逻辑电路里边的回门与门和非门。我们把 sigmoid 函数换成下面的符号函数,传统的神经网络立即编程逻辑电路。
s i g n ( x ) = { 1 , ( x > 0 ) 0 , ( x ≤ 0 ) (1) \tag1 sign(x)=\begin{cases} 1,\ (x \gt 0)\\ 0, \ (x \le 0) \end{cases} sign(x)={1, (x>0)0, (x≤0)(1)
显然如果x,y取值为0,1,下面关系成立:
x ∧ y = s i g n ( x + y − 1.5 ) x ∨ y = s i g n ( x + y − 0.5 ) ¬ x = 1 − x (2) \tag2 x \land y = sign(x + y - 1.5)\\ x \lor y = sign(x + y - 0.5) \\ \lnot x = 1 - x x∧y=sign(x+y−1.5)x∨y=sign(x+y−0.5)¬x=1−x(2)
2. 模数(AD)转换机制
在使用逻辑电路的时候,首先呢,我们需要把模拟的输入量变成0和1这样的布尔值,所以呢,在传统的这个数字电路当中呢,就有一个模数转换电路,这层电路是非常关键的,那么在这之后的话才会有纯正的数字电路设计。
神经网络呢,实际上也有这样一个类似的过程。一般来讲,一个神经元它代表着是利用一个超平面把空间分成两部分,能够判断这个样本是落在了超平面的哪一半。因此我们说一个神经元,实际上它等于说把这个现实世界空间坐标的这样一个模拟的量啊,利用和超平面的这样一个位置关系,转化成了0、1,这样的一个布尔值,实际上就是起到模数转换作用,参见下面的的代数式。
y = s i g n ( w 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n ) (3) \tag3 y=sign(w_0+w_1x_1+w_2x_2+...+w_nx_n) y=sign(w0+w1x1+w2x2+...+wnxn)(3)
3. 神经网络和逻辑电路的本质区别
如果神经网络和逻辑电路是一回事,那么我们现在做的所有工作都毫无意义了,所以呢,我们必须得探讨一下它们两者之间呢,有什么本质性的区别。
首先呢,一个最重要的区别是什么呢?这个逻辑电路在设计的时候,它首先需要给出一个真值表,也就是输入和输出之间的关系,必须得采用暴力穷举的方式完完全全地列举出来,中间少那么一条,这个逻辑电路也设计不出来的。
那么神经网络,它所处的这样一个应用环境啊应用场景实际上是没有办法把所有可能的输入输出全部暴力穷举出来的,那也就是说呢,我们需要在这个真值表而残缺的情况下,那怎么样合理的来设计这样一个电路,因此呢,从这个模型设计的方法上来看。神经网络呢,他和逻辑电路有着一个质的区别,逻辑电路呢,是在信息完完全全充分提供的条件下,对吧,就是我的训练样本呢,已经包含了所有的各种情况,一条我都没有落下,那这个时候我们就可以采用逻辑电路的方式来实现啊,我们利用布尔代数理论很容易把这个电路设计出来。
那么神经网络它所面对的场景呢,这往往是我们的训练样本,仅仅呢是占所有可能让人当中的极小的一部分啊,那么我们要利用这非常不充分的这样一个信息来推测呢,这个整体的网络应该怎么样去设计?这是神经网络要面对的一个重要的问题,这也是他的网络的设计方式和传统的逻辑电路呢,出现一个本质性的区别。
4. sigmoid 函数的意义
那么神经网络和逻辑电路的这样一个本质性的区别,那么就决定了神经网络的设计方法,必须呢另辟蹊径,所以我们现在用的这样一个梯度下降的方法来求神经网络,它本质上就是讲呢,我首先呢,随机的给出这样一个网络结构,然后呢,我用这个训练样本的输入X来预测他的Y值,那我的预测的Y值呢和真实的位置来做一个比较。我看两个差距有多大,这个然后的话我去调整这个神经网络的参数,让看往哪个方向调整,那么使得预测值呢,和真正的那个外侄呢差距呢,会逐渐的变小,这样最后的话,我能够通过调整参数让二者的差距呢,能够最小化,这样呢就达到了我的这样一个设计的目的。
按照这个思路的话,我就希望在调整神经网络参数的时候,能随时看到我的输出的Y值和真实的Y值之间差距的变化。
那么采用符号函数sign来做这样一个逻辑运算,或者是实现那个模拟量到数字量的这样一个转换啊,实际上是有问题的,为什么呢,它就像那个学生考试一样,如果我们那个考试的成绩只有及格和不及格两个分数的话,那么学生呢,他改进了学习方法,然后重新考试,那么比如说第一次是不及格,第二次还是不及格,那这个学生他显然不知道自己是进步了,还是退步了。
所以我们希望这个转换函数啊,它能够实现了从零到一之间的一个平滑的过度啊,那这样的话我们就能够呢,根据自变量变化,在自变量发生少量的变化,他的输出呢,也会随着呢发生少量的变化,那这样呢,我们就能看出呢,模型参数变化对输出的这个细微的影响。参见下图:
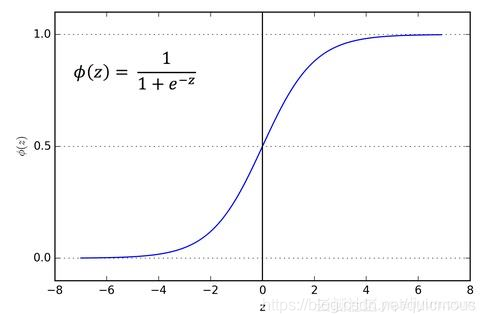
5. 激活函数的哲学思想
那么刚才我们看到了这个sigmoid函数和符号函数之间他们的一点区别,符号函数呢,实现了零到一之间的一个跃阶的这样一个变化,当X小于等于零的时候,它的输出就是0,X大于0的时候呢,输出结果一下子就跳到1上去了,他实现了这样一个变化。而这个sigmoid函数,他把这个变化过程平滑了。这个好处,就是说,当这个参数发生细微的变化的时候呢,我们的输出也会跟着产生一个细微的变化,而符号函数就不具备这个功能。
那么就这么一点儿细微的区别,实际上,导致了神经网络和传统的逻辑电路设计上的一个重大的区别,那么如果采用符号函数的话,那么神经网络就等价于神经网络,它呢,只能是靠人工呢,根据真值表来进行设计,把符号函数换成sigmoid函数,这个最终的设计方案就可以利用机器学习的方法来实现。因此我们讲啊,这个在这个神经元后面的转换函数换成了sigmoid以后啊,那么这个神经元它就具有活性了。原来是死的,和与门、或门、非门一样,要靠人工来进行设计啊,他是一个没有生命力的一个。换成 sigmoid 后,神经网络可以摆脱人工设计,采用机器学习的方法自动寻找最佳的设计方案了。
那么在分类网络的最后一层的激活函数,我们一般选用softmax。其实大家想过没有,为什么这一层不直接用one-hot编码?就是说最大的那个输出,我们直接变成1其他的都是0.如果最后直接采用one-hot编码的话,那这个和我们讲的神经元后边跟上一个符号函数,实际上就非常相似,对吧?你最大的那个是1,其他都是0,那么当我的参数呢,做了一个微小的调整以后,那你这个输出结果很可能根本就不会跟着发生变化,对吧?那我们采用softmax以后我们就会发现,那么你最大的那一个输出分量和其他的输出分量,在参数调整以后都会跟着发生微小的变化,这样我们就能知道,我们的结果是在朝好的方向去变,还是在朝差的方向去变。
激活函数,使得神经元、神经网络有了活力,能像生命体一样自己通过学习、进化,最终完成自我设计,这就是神经网络设计技术与逻辑电路设计技术之间的根本区别。
6. 逻辑电路是神经网络的特殊情况
最后就不多啰嗦了。我觉得呢,这个数字e,我们知道他大约等于2.718,对吧?如果我们假设它是一个可以变的,我们令 e 趋向无穷大,实际上我们就会发现sigmoid函数,它就会变成符号函数。
lim e → ∞ s i g m o i d ( x ) = s i g n ( x ) \lim_{e \to \infty}sigmoid(x) = sign(x) e→∞limsigmoid(x)=sign(x)
另外
o n e h o t ( x 1 , x 2 , . . . , x n ) = ( x 1 = m a x ( x 1 , . . . , x n ) , x 2 = m a x ( x 1 , . . . , x n ) , . . . , x n = m a x ( x 1 , . . . , x n ) ) onehot(x_1,x_2,...,x_n)=(\\ x_1=max(x_1,...,x_n),\\ x_2=max(x_1,...,x_n),\\ ...,\\ x_n=max(x_1,...,x_n)\\ ) onehot(x1,x2,...,xn)=(x1=max(x1,...,xn),x2=max(x1,...,xn),...,xn=max(x1,...,xn))
显然,
lim e → ∞ s o f t m a x ( x 1 , . . . , x n ) = o n e h o t ( x 1 , . . . , x n ) \lim_{e \to \infty}softmax(x_1,...,x_n) = onehot(x_1,...,x_n) e→∞limsoftmax(x1,...,xn)=onehot(x1,...,xn)
在极限情况下,神经网络就变成了传统的逻辑电路,你觉得神奇吧?
这篇关于神经网络和逻辑电路——表面相同的设计形式,天壤之别的设计思想的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




