本文主要是介绍数据结构【八】- 递归【一】递归的本质/ 递归的宏观语意/ 写递归算法的基本原则/ 递归函数的“微观”解读,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一。递归的本质
本质上,递归就是将原来的问题,转化为更小的同一问题。
二。递归的举例
更多链表问题搜索:LinkedListProblems.pdf
(一)例子
用递归来写数组求和
(二)思路
1. 对一个数组求和就等于:将【数组总和】=【数组的第0个数】+【数组中从1索引到...n-1这个索引的和】。
- 这个时候,Sum(arr[1....n-1])要解决的问题就要比Sum(arr[0....n-1]要解决的问题更小。==> 这就是更小的同一问题。
- 为什么更小?==> 因为Sum(arr[1....n-1])少了一个元素,只需要对n-1个元素求和。
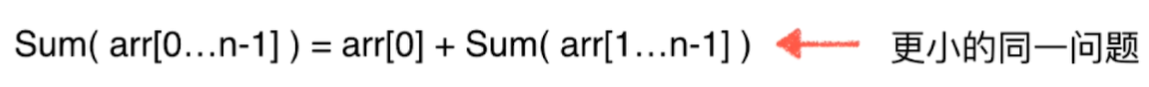
2. 以此类推:【Sum(arr[1....n-1])】= 【索引为1的元素】+【数组中从2索引到...n-1这个索引的和】

3. 直到在最后的时候,我们这个问题缩小到:【Sum(arr[n-1....n-1])】=【索引为n-1的元素】+【空数组】
【空数组】的和为0,至此我们得到了一个基本的问题
![]()
(三)数组求和代码
public class ArraySum {public static int sum(int[] arr){return sum(arr,0);}//计算arr[l...n]这个区间内所有数字的和private static int sum(int[] arr, int l){//基本问题:当l==arr.length的时候,也就是数组为空if (l == arr.length){return 0;}return arr[l]+sum(arr, l+1);}
}(四)代码测试
public static void main(String[] args){int[] nums = {1,2,3,4,5,6,7,8};System.err.println(sum(nums));}36
(四)递归函数的“微观”解读
- 递归函数的调用,本质就是函数调用。
1. 递归调用方法
对于数据arr = [6,10] ,我们用sum()方法求它的总和。

2. 递归运行过程:
我们给数组【arr = [6,10]】来调用方法 sum(arr,0);
第一步:
l此时等于0,那么我们运行到 【int x = sum(arr,l+1);】的时候,就产生了递归调用。重新调用了一下sum(arr,0+1).

第二步: l此时等于1。调用sum(arr,1),也就是在一个新的sum函数中,重新针对现在的参数走一遍。进入方法sum(arr,1),运行到 【int x = sum(arr,l+1);】的时候2产生了递归调用。重新调用了一下sum(arr,1+1).

第三步:l此时等于2。调用sum(arr,2),进入方法sum(arr,2),运行到 【if (l == arr.length) return 0;】的时候,满足这个条件,【return 0】;

第四步:此时sum(arr,2)中返回的【0】就返回到上一次在sum(arr,1)这次调用中中断的位置,也就是【int x = sum(arr,l+1);】.
此时x可以计算出来【x是0】.然后我们可以计算出sum(arr,1)的res的值【res是10+0=10】


第五步:此时sum(arr,1)中返回的【10】就返回到上一次在sum(arr,0)这次调用中中断的位置,也就是【int x = sum(arr,l+1);】。
此此时x可以计算出来【x是10】.然后我们可以计算出sum(arr,0)的res的值【res是6+10=16】


第六步:最后得出sum(arr,0)的结果是16.

三。写递归算法的基本原则
1. 所有的递归算法都可以分成两部分
- 求解最基本的问题(最基本的问题是不能自动求解的,是需要我们自己编写逻辑来求解)
- 核心部分:将原问题转化为更小的问题

2. 写递归函数的时候要注重:递归函数的“宏观”语意。站在更高的层次去思考这个函数本身的功能和作用,有利于理解递归的逻辑。
对于【数组求和】来说,我们“宏观”语意就是:计算arr[] 数组的“l”到“n”的索引的和。
对于【删除链表元素】来说,宏观语意就是:对一个链表中删除值为val的节点
3. 不要太注意内部调用。
4. 递归函数的调用,本质就是函数调用。只不过调用的函数是自己而已。
5. 递归调用是有代价的:
函数调用需要更多的时间开销,包括
【1】记录当前函数执行的位置+当前局部变量的状态,
【2】函数调用本身在计算机底层要找到新的函数所在的位置。
更重要的:递归调用消耗系统栈的空间。
【1】例如,当不处理基本问题时,递归将一直进行下去,没有终止,最终产生错误:系统栈被占满.
【2】如果对于数百万的数组用递归算法求和,栈空间不够用。
【3】如果对百万长度的链表递归删除元素,栈空间不够用。
以上所有内容都是通过"慕课网"听"liuyubobobo"的《玩转数据结构》课程后总结
这篇关于数据结构【八】- 递归【一】递归的本质/ 递归的宏观语意/ 写递归算法的基本原则/ 递归函数的“微观”解读的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







