【图与网络数学模型】1.Dijkstra算法求解最短路径问题

本文主要是介绍【图与网络数学模型】1.Dijkstra算法求解最短路径问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

一、图论基本概念

1. 图论

图论是应用非常广泛的运筹学分支，它已经广泛地应用于物理学控制论、信息论、工程技术、交通运输、经济管理、电子计算机等各项领域。对于科学研究、市场和社会生活中的许多问题，可以用图论的理论和方法来加以解决。

2. 哥尼斯堡七桥问題

关于图的第一篇论文是瑞士数学家欧拉（E. Euler）在1736年发表的解决“哥尼斯堡” 七桥难题的论文。

要如何走过每座桥恰一次，再返回出发点？

即能否从某一点开始不重复地一笔画出这个图形，最终回到原点。欧拉在他的论文中证明了这是不可能的，因为这个图形中每一个顶点都与奇数条边相连接，不可能将它一笔画出，这就是古典图论中的第一个著名问题。

3. 图的一些基本概念

图论中的图是由点、点与点之间的线所组成的。

涉及的一些概念如下表，在此不做赘述。

点	边	图	链
点	边，弧	无向图	链
端点	关联边	有向图	圈
始点，终点	多重边	简单图	初等链/圈
度（次）	环	多重图	简单链/圈
奇点，偶点		连通图	基础图
悬挂点	悬挂边	不连通图	路
弧立点			回路

4. 图的矩阵表示

邻接矩阵 Adjacency matrix

• 表示图中两点之间的相互关系
• 两点之间有弧或边的，用1表示，否则用0表示，构成一个矩阵A

上图可用矩阵表示如下：

二、最短路径问题算法

最短路径问题是图论中十分重要的最优化问题之一，它作为一个经常被用到的基本工具，可以解决生产实际中的许多问题，也可以用于解决其它的最优化问题。

如果P是D中从 $v_s$ 到 $v_i$ 的最短路， $v_i$ 是 P 中的一个点，那么从 $v_s$ 沿 P 到 $v_i$ 的路是从 $v_s$ 到 $v_i$ 的最短路。

1. 图形的标号法

求下图从A到G的最短路：

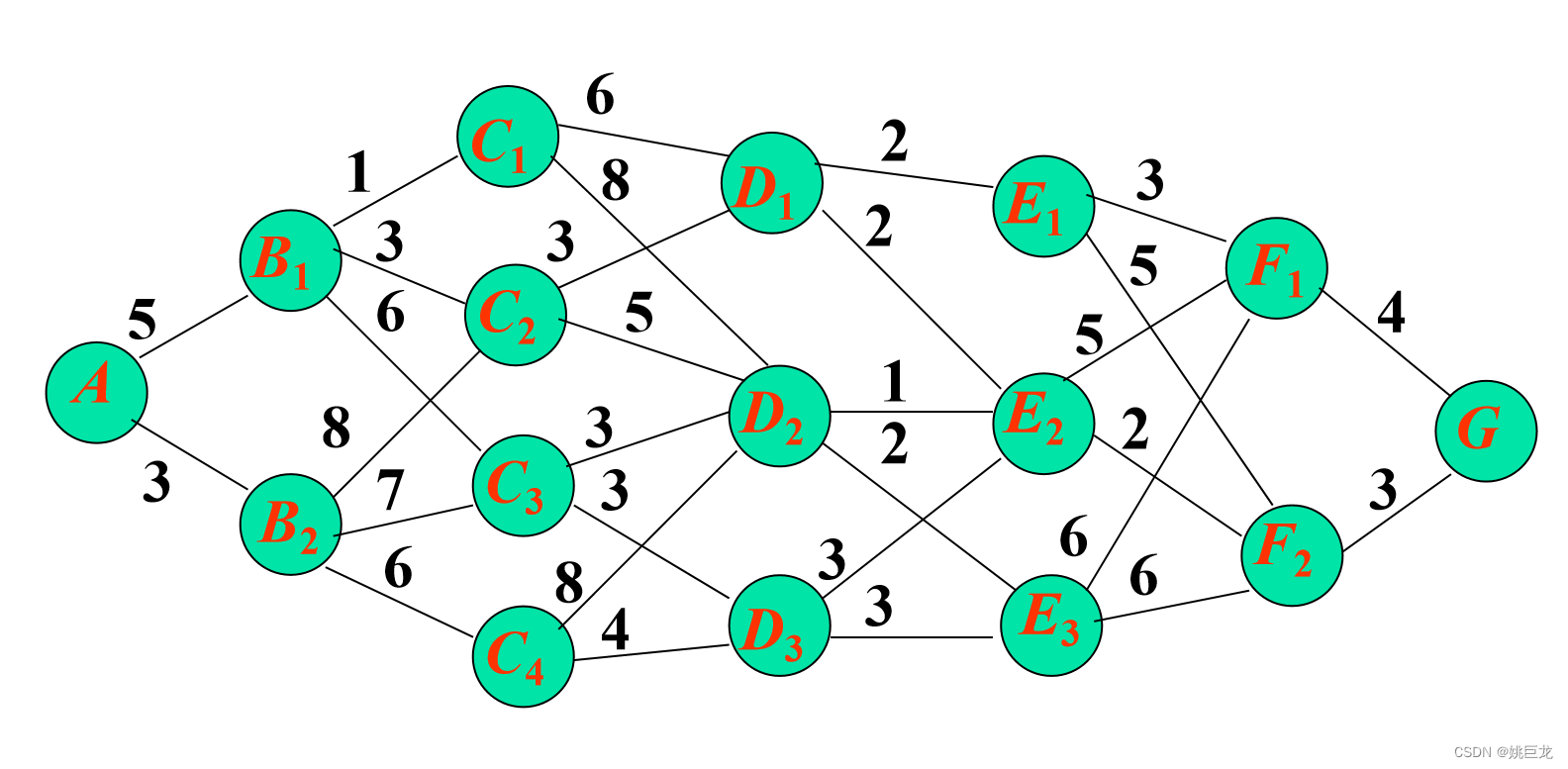
解法：先标出离终点最近的一段，然后标号与该点距离最短的点，继续逆推至始点。

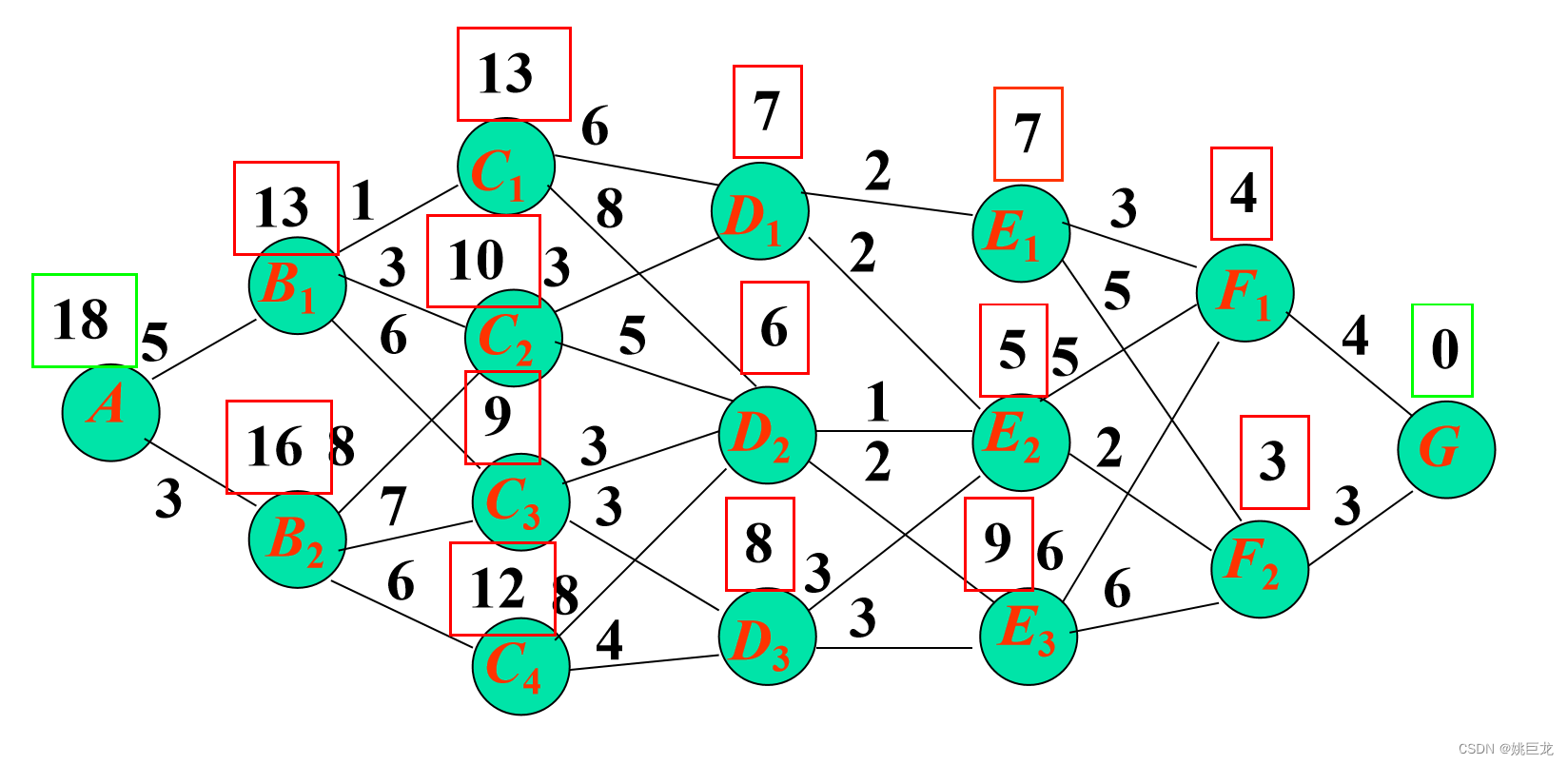
从A到G的最短路为： A - B1-C2-D1-E2-F2-G

2. Dijkstra法

（1）基本思路

从$v_s$出发，逐步地向外探寻最短路。

执行过程中，与每个点对应，记录下一个数 (称为此点的标号)

1. 它或者表示从$v_s$到该点的最短路的权 (称为P标号)
2. 或者是从$v_s$到该点的最短路的权的上界 (称为T标号)

方法的每一步是修改T标号，并且把某一个具T标号的点改变为具P标号的点，从而使D中具P标号的点多一个，如此经过 p-1步，就可以求出从$v_s$到各点的最短路。

（2）求解示例

例如求下图从1到8的最短路径：

1. X={1}, $w_1$=0
   

2. X={1,4}
   

3. X={1,2,4}
   

4. X={1,2,4,6}
   

5. X={1,2,4,6,7}
   

6. X={1,2,3,4,6,7}
   

7. X={1,2,3,4,6,7,8}
   
   1到8的最短路径为{1，4，7，5，8}，长度为10。

三、基于Python的Dijkstra算法

1. 创建图对象

创建一个图对象：接受一个参数 vertices，表示图中顶点的数量。

在初始化过程中，将顶点数量存储在 self.V 中，并创建一个二维数组 self.graph 作为邻接矩阵，初始值为0。

	def __init__(self, vertices):self.V = verticesself.graph = [[0 for column in range(vertices)]for row in range(vertices)]

2. 打印最短路径

printSolution(self, dist)：接受一个参数 dist，该参数是一个包含各个顶点距离源点的最短距离的列表。

遍历所有顶点，打印每个顶点及其距离源点的最短距离。

	def printSolution(self, dist):print("Vertex \t Distance from Source")for node in range(self.V):print(node, "\t\t", dist[node])

3. 查找顶点

查找未包含在最短路径树中的距离源点最近的顶点。

minDistance(self, dist, sptSet)：接受两个参数 dist 和 sptSet，分别表示从源点到各个顶点的当前最短距离和是否已经包含在最短路径树中。

遍历所有顶点，找到距离源点最近且未包含在最短路径树中的顶点，并返回其索引。

	def minDistance(self, dist, sptSet):min = 1e7for v in range(self.V):if dist[v] < min and sptSet[v] == False:min = dist[v]min_index = vreturn min_index

4. Dijkstra 算法实现

参数 src：表示源点的索引。

初始化距离源点的距离列表 dist 和最短路径树标记列表 sptSet。

在循环中，选择距离源点最近且未包含在最短路径树中的顶点作为当前顶点 u，将其标记为已经包含在最短路径树中。

更新与当前顶点相邻且未包含在最短路径树中的顶点的距离，如果新的距离小于之前记录的距离，则更新距离值。

最后调用 printSolution 方法打印结果。

	def dijkstra(self, src):dist = [1e7] * self.Vdist[src] = 0sptSet = [False] * self.Vfor cout in range(self.V):u = self.minDistance(dist, sptSet)sptSet[u] = Truefor v in range(self.V):if (self.graph[u][v] > 0 andsptSet[v] == False anddist[v] > dist[u] + self.graph[u][v]):dist[v] = dist[u] + self.graph[u][v]self.printSolution(dist)

5. 完整程序运行

求下图从1到8的最短路径：

class Graph():def __init__(self, vertices):self.V = verticesself.graph = [[0 for column in range(vertices)]for row in range(vertices)]def printSolution(self, dist):print("Vertex \t Distance from Source")for node in range(self.V):print(node, "\t\t", dist[node])def minDistance(self, dist, sptSet):min = 1e7for v in range(self.V):if dist[v] < min and sptSet[v] == False:min = dist[v]min_index = vreturn min_indexdef dijkstra(self, src):dist = [1e7] * self.Vdist[src] = 0sptSet = [False] * self.Vfor cout in range(self.V):u = self.minDistance(dist, sptSet)sptSet[u] = Truefor v in range(self.V):if (self.graph[u][v] > 0 andsptSet[v] == False anddist[v] > dist[u] + self.graph[u][v]):dist[v] = dist[u] + self.graph[u][v]self.printSolution(dist)g = Graph(8)
g.graph = [[0, 2, 0, 1, 0, 3, 0, 0],[0, 0, 6, 0, 5, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 6],[0, 10, 0, 0, 0, 0, 2, 0],[0, 0, 9, 0, 0, 0, 0, 4],[0, 0, 0, 5, 0, 0, 4, 0],[0, 7, 0, 0, 3, 0, 0, 8],[0, 0, 0, 0, 0, 0, 0, 0]]g.dijkstra(0)

输出结果如下：

Vertex 	 Distance from Source
0 		 0
1 		 2
2 		 8
3 		 1
4 		 6
5 		 3
6 		 3
7 		 10

1-8最短路径的长度为10.

这篇关于【图与网络数学模型】1.Dijkstra算法求解最短路径问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---