本文主要是介绍【MATLAB源码-第139期】基于matlab的OFDM信号识别与相关参数的估计,高阶累量/小波算法调制识别,循环谱估计,带宽估计,载波数目估计等等。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
操作环境:
MATLAB 2022a
1、算法描述
在现代无线通信系统中,正交频分复用(OFDM)因其高效的频谱利用率、强大的抗多径衰落能力以及灵活的带宽分配等优势,成为了一种非常重要的调制技术。然而,随着无线通信网络的复杂性增加,对OFDM信号的识别与参数估计提出了更高的要求。这不仅是为了提高通信质量和效率,也是为了确保网络的兼容性和安全性。因此,研究OFDM调制识别和参数估计算法具有重要的理论意义和实际应用价值。
OFDM调制识别
OFDM调制识别主要是区分OFDM信号和其他类型信号(如单载波调制信号)的过程,这对于无线通信系统的信号处理和资源分配等方面具有重要意义。研究中涉及到的调制识别算法主要包括基于高阶累量的方法和基于小波变换的方法。
基于高阶累量的识别算法
高阶累量是信号统计特性的一种,可以用来描述信号的非高斯性和非线性特性。通过计算接收信号的高阶累量,可以得到一些关键的统计特征,这些特征可以用于区分OFDM信号和单载波调制信号。该方法的优势在于不需要信号的先验知识,但在低信噪比(SNR)条件下,其性能可能会受到影响。
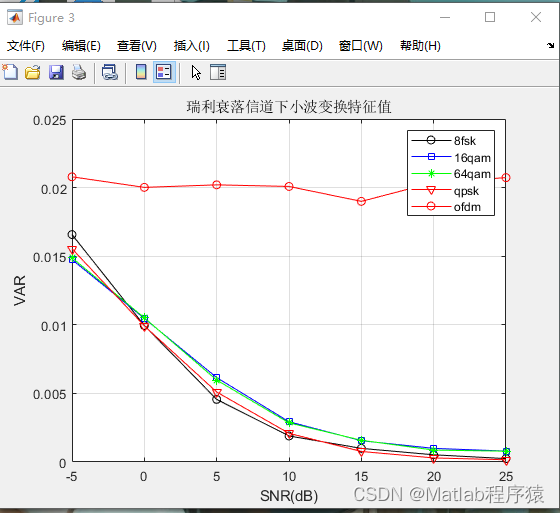
基于小波变换的识别算法
小波变换是一种时间-频率分析工具,能够提供信号的时频特性。通过对信号进行小波变换,可以有效地提取信号的局部特征,进而用于区分OFDM信号和单载波调制信号。该方法适用于复杂的信道条件,包括高斯信道和多径瑞利衰落信道,能够在多种环境下实现准确的信号识别。
OFDM参数估计
对于OFDM信号,参数估计是一个关键步骤,涉及到带宽、载频、有效数据长度、符号总长度、循环前缀长度和子载波间隔等多个参数的确定。这些参数的准确估计对于OFDM系统的设计和优化至关重要。
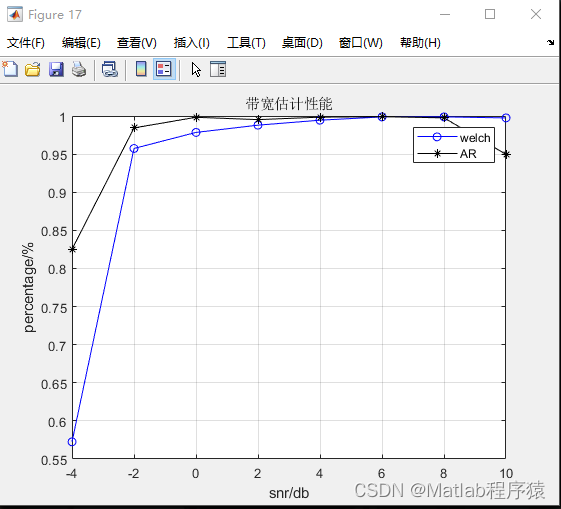
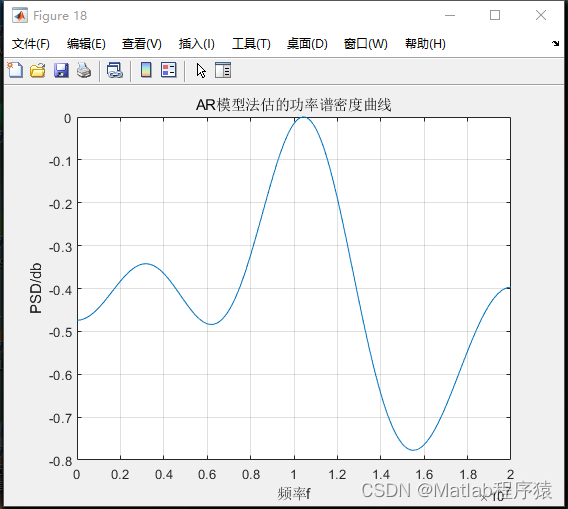
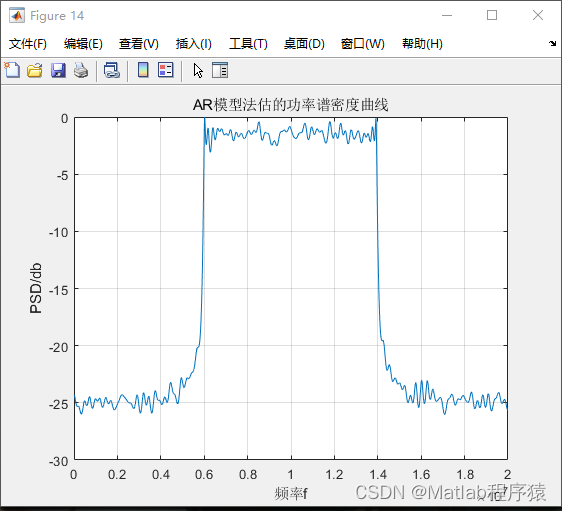
基于功率谱的带宽估计
功率谱分析是估计信号带宽的一种常用方法。通过使用Welch算法或AR模型法求解信号的功率谱,可以估计出OFDM信号的带宽。这两种方法各有优劣,Welch算法简单易实现,但在某些情况下可能不够精确;而AR模型法可以提供更高的频谱分辨率,但计算复杂度较高。
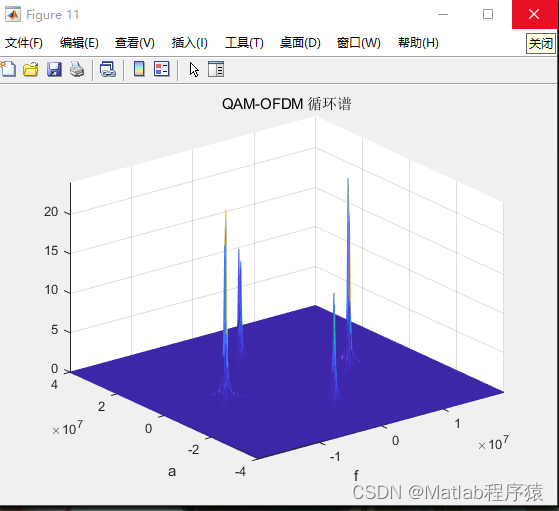
基于循环谱的载频估计
循环谱分析利用信号的循环平稳性质,可以有效地估计载频。这种方法适用于OFDM信号,因为OFDM信号具有明显的循环平稳特性。通过分析信号的循环谱,可以准确地确定载频,这对于信号解调和进一步的信号处理非常重要。
基于自相关的有效数据长度、符号总长度和循环前缀长度估计
自相关方法是基于信号的时间域特性进行参数估计的一种方法。通过计算信号的自相关函数,并结合FFT(快速傅里叶变换),可以估计出OFDM信号的有效数据长度、符号总长度和循环前缀长度。这种方法既可以使用可变延时自相关,也可以使用固定延时自相关,根据信号的特性选择最合适的方法。
子载波数目估计
子载波数目的估计对于OFDM信号的解调和信号重构非常关键。研究中提出了基于带宽估计和基于过采样的两种子载波数目估计算法。这些算法能够在不同的信道条件下(如高斯信道和多径瑞利衰落信道)准确估计子载波的数目。
仿真分析
为了验证上述识别和参数估计算法的有效性,进行了大量的仿真实验。这些实验不仅考虑了理想的高斯信道条件,还模拟了实际通信中常见的多径瑞利衰落信道条件。通过比较不同算法在各种信道条件下的性能,可以得出各算法的优缺点和适用范围,为OFDM系统的设计和优化提供了重要的参考依据。
总的来说,OFDM调制识别和参数估计是确保高效、可靠通信的关键技术。通过深入研究这些算法,并结合仿真实验进行验证,可以为无线通信系统的发展提供坚实的技术支撑。
2、仿真结果演示







3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
这篇关于【MATLAB源码-第139期】基于matlab的OFDM信号识别与相关参数的估计,高阶累量/小波算法调制识别,循环谱估计,带宽估计,载波数目估计等等。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



