题目名称 | 时空定位 | 棋子移动 | 高精度乘法 | 数独游戏 |
存盘文件名 | location | piece | mul | sudoku |
输入文件名 | location.in | piece.in | mul.in | sudoku.in |
输出文件名 | location. out | piece.out | mul.out | sudoku.out |
时限 | 1s | 1s | 1s | 1s |
内存限制 | 64MB | 64MB | 64MB | 64MB |
题1 时空定位(location)
【题目描述】
张琪曼已经确定了李旭琳在一个长为20千米,宽为2千米的空间,她要在横中心线上放置半径为Ri的定位装置,每个定位装置的效果都会让以它为中心的半径为实数Ri(0<Ri<15)的物体被定位,这有充足的定位装置i(1<i<600)个,并且一定能把空间全部覆盖,你要做的是:选择尽量少的定位装置,把整个空间全部覆盖。
【输入格式】
第一行m表示有m组测试数据。
每一组测试数据的第一行有一个整数数n,n表示共有n个定位装置,随后的一行,有n个实数Ri,Ri表示该定位装置能覆盖的圆的半径。
【输出格式】
输出所用装置的个数。
【输入样例】
2
5
2 3.2 4 4.5 6
10
1 2 3 1 2 1.2 3 1.1 1 2
【输出样例】
2
5
这道题就是肥肠简单的贪心,来看我的AC代码吧:
1 #include<bits/stdc++.h>
2 using namespace std;
3 double a[601];
4 int main()
5 {
6 //freopen("location.in","r",stdin);
7 //freopen("location.out","w",stdout);
8 int m,n,ans;cin>>m;
9 for(int i=0;i<m;i++)
10 {
11 double l=20;ans=0;
12 cin>>n;
13 for(int j=0;j<n;j++)cin>>a[j];
14 sort(a,a+n);
15 for(int j=n-1;j>=0;j--)
16 {
17 ans++;
18 double x=sqrt(a[j]*a[j]-1);
19 l-=2*x;
20 if(l<=0)break;
21 }
22 cout<<ans<<endl;
23 }
24 return 0;
25 }
题2 棋子移动(piece)
【问题描述】
魔法世界的历史上曾经出现过一位赫赫有名的不败战神陈庆之,陈庆之以棋道悟兵法,一生身经数百战,没有一场败绩,而且没有一场不是在绝对的劣势中大胜敌军。
受此影响,魔法世界开始流行一种叫棋子移动的游戏,即有2N个棋子(N≥4)排成一行,开始位置为白子全部在左边,黑子全部在右边,例如当N=4时,棋子排列情况为:
〇〇〇〇●●●●
移动棋子的规则是:每次必须同时移动相邻两个棋子,颜色不限,可以左移也可以右移到空位上去,但不能调换两个棋子的左右位置.每次移动必须跳过若干个棋子(不能平移),要求最后能移成黑白相间的一行棋子。例如当N=4时,最终排列情况为:
〇●〇●〇●〇●
试求出移动步骤。
【输入格式】
一个整数,即N。
【输出格式】
输出移动步骤,每一步操作占一行。
【输入样例】
4
【输出样例】
4,5-->9,10
8,9-->4,5
2,3-->8,9
7,8-->2,3
1,2-->7,8
分治算法经典例题啦(~ ̄▽ ̄)~ 把所有情况都转化成n=4的情况就可以啦
上代码:
1 #include<bits/stdc++.h>
2 using namespace std;
3 int k;
4 void move(int j)
5 {
6 printf("%d,%d-->%d,%d\n",j,j+1,k,k+1);
7 k=j;
8 }
9 void mv(int n)
10 {
11 if(n==4)
12 {
13 move(4);move(8);move(2);move(7);move(1);
14 }
15 else
16 {
17 move(n);move(2*n-1);mv(n-1);
18 }
19 }
20 int main()
21 {
22 //freopen("piece.in","r",stdin);
23 //freopen("piece.out","w",stdout);
24 int n;cin>>n;k=2*n+1;
25 mv(n);
26 return 0;
27 }
题3 高精度乘法(mul)
【题目描述】
输入两个整数,求它们的乘积并输出。
【输入格式】
两行,每行表示一个非负整数(不超过5000位)
【输出格式】
两数的乘积。
【输入样例】
99
101
【输出样例】
9999
高精运算肥肠重要,所以这些模板就算是背也要背下来哇!
1 #include<bits/stdc++.h>
2 using namespace std;
3 int a[5001],b[5001],c[10010];
4 void init(int x[])
5 {
6 string s;
7 cin>>s;
8 x[0]=s.length();
9 for(int i=0;i<x[0];i++)x[x[0]-i]=s[i]-'0';
10 while(x[x[0]]==0&&x[0]>1)x[0]--;
11 }
12 int main()
13 {
14 //freopen("mul.in","r",stdin);
15 //freopen("mul.out","w",stdout);
16 init(a);init(b);
17 int x=0;
18 for(int i=1;i<=a[0];i++)
19 {
20 x=0;
21 for(int j=1;j<=b[0];j++)
22 {
23 c[i+j-1]=c[i+j-1]+x+a[i]*b[j];
24 x=c[i+j-1]/10;
25 c[i+j-1]%=10;
26 }
27 if(x)c[i+b[0]]=x;
28 }
29 c[0]=a[0]+b[0];
30 while(c[c[0]]==0&&c[0]>1)c[0]--;
31 for(int i=c[0];i>=1;i--)cout<<c[i];
32 return 0;
33 }
题4 数独游戏(sudoku)
【问题描述】
“我陪你玩这个数独游戏已经整整三天了,你到底什么时候给我上古神器?”修罗王忍不住问。
“这人生啊,急也好,慢也好,目标总能达到,何不让自己静下心来,慢慢欣赏一下沿途的风景?”上古神器的守护者悠悠道。
修罗王悻悻道:“如果玩这个没有赌注的话,我还真信你的话了,就三天工夫,你都把我的魔法石赢去一大半了。”
已知9×9的方阵,有些格子填有1~9的数字,有的格子则是空白。你的任务是完成这个方阵,使得每一行、每一列以及每一个小九宫格中的数字都刚好是1~9。
如图所示,该例子中左图是开始时的方阵状态,右图为完成后的样子。
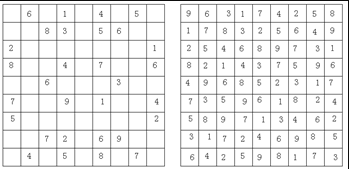
【输入格式】
9行9列的方阵状态,0代表空格。
【输出格式】
输出完成后的方阵状态,每一个小九宫格以空格分隔。行为三个空格,列为一个空格。
【输入样例】
0 6 0 1 0 4 0 5 0
0 0 8 3 0 5 6 0 0
2 0 0 0 0 0 0 0 1
8 0 0 4 0 7 0 0 6
0 0 6 0 0 0 3 0 0
7 0 0 9 0 1 0 0 4
5 0 0 0 0 0 0 0 2
0 0 7 2 0 6 9 0 0
0 4 0 5 0 8 0 7 0
【输出样例】
9 6 3 1 7 4 2 5 8
1 7 8 3 2 5 6 4 9
2 5 4 6 8 9 7 3 1
8 2 1 4 3 7 5 9 6
4 9 6 8 5 2 3 1 7
7 3 5 9 6 1 8 2 4
5 8 9 7 1 3 4 6 2
3 1 7 2 4 6 9 8 5
6 4 2 5 9 8 1 7 3
这道题的输出格式很重要滴!至于算法思想就是深搜嘛。其实我写的是比较暴力粗糙的,其实明明可以进行剪枝的...不过反正我AC啦!
1 #include<bits/stdc++.h>
2 using namespace std;
3 struct node{
4 int shu,jn;
5 }a[10][10];
6 struct kong{
7 int xx,yy;
8 }ko[82];
9 int h[10][10],l[10][10],jiu[10][10],m;
10 void print()
11 {
12 for(int i=1;i<=9;i++)
13 {
14 if(i==4||i==7)cout<<endl;
15 for(int j=1;j<=9;j++)
16 {
17 if(j==4||j==7)cout<<" ";
18 cout<<a[i][j].shu<<" ";
19 }
20 cout<<endl;
21 }
22 }
23 void search(int n)
24 {
25 int x=ko[n].xx,y=ko[n].yy;
26 if(n==m+1)
27 {
28 print();exit(0);
29 }
30 if(x&&y)
31 for(int i=1;i<=9;i++)
32 {
33 if(h[x][i]==0&&l[y][i]==0&&jiu[a[x][y].jn][i]==0)
34 {
35 ko[n].xx=0;
36 ko[n].yy=0;
37 a[x][y].shu=i;
38 h[x][i]=1;
39 l[y][i]=1;
40 jiu[a[x][y].jn][i]=1;
41 search(n+1);
42 ko[n].xx=x;
43 ko[n].yy=y;
44 a[x][y].shu=0;
45 h[x][i]=0;
46 l[y][i]=0;
47 jiu[a[x][y].jn][i]=0;
48 }
49 }
50 else search(n+1);
51 }
52 int main()
53 {
54 //freopen("sudoku.in","r",stdin);
55 //freopen("sudoku.out","w",stdout);
56 int x=1,k=0,n=1;
57 for(int i=1;i<=9;i++)
58 {
59 if(i==1||i==4||i==7)x=i;
60 else x-=2;
61 for(int j=1;j<=9;j++)
62 {
63 if(j==4||j==7)x++;
64 cin>>a[i][j].shu;
65 a[i][j].jn=x;
66 if(a[i][j].shu)
67 {
68 h[i][a[i][j].shu]=1;
69 l[j][a[i][j].shu]=1;
70 jiu[a[i][j].jn][a[i][j].shu]=1;
71 }
72 else
73 {
74 m++;
75 ko[m].xx=i;
76 ko[m].yy=j;
77 }
78 }
79 }
80 search(1);
81 return 0;
82 }