数据结构与算法：二叉树（寻找最近公共祖先、寻找后继节点、序列化和反序列化、折纸问题的板子和相关力扣题目）

本文主要是介绍数据结构与算法：二叉树（寻找最近公共祖先、寻找后继节点、序列化和反序列化、折纸问题的板子和相关力扣题目），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最近公共祖先

第一版（前提：p和q默认存在于这棵树中）

可以层序遍历每个节点时用个HashMap存储该结点和其直接父节点的信息。然后从p开始溯源，将所有的父节点都添加到一个HashSet集合里。然后从q开始溯源，每溯源一步看是否在set集合中，在的话就返回。

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {HashMap<TreeNode, TreeNode> fatherMap = new HashMap<>();//充当父指针的作用，第一个Node的父亲是第二个NodefatherMap.put(root,root);getFather(root, fatherMap);HashSet<TreeNode> set1 = new HashSet<>();//存放从p开始向上溯源的一系列父节点（包括p自己）TreeNode cur = p;while(fatherMap.get(cur)!=cur){//没有溯源到root节点set1.add(cur);cur = fatherMap.get(cur);}set1.add(root);//最后的root节点也要加上cur = q;while(!set1.contains(cur)) cur = fatherMap.get(cur);//从q开始向上溯源，每溯源一步，就检查是否在set1中//最后得到的cur就是最近公共祖先return cur;}//帮每个节点找父节点的过程public void getFather(TreeNode root,HashMap<TreeNode, TreeNode> fatherMap){if(root==null) return;fatherMap.put(root.left, root);fatherMap.put(root.right, root);getFather(root.left, fatherMap);getFather(root.right, fatherMap);}

可以看到效率很低，12ms，击败7.89%使用 Java 的用户。

第二版（前提：p和q默认存在于这棵树中）

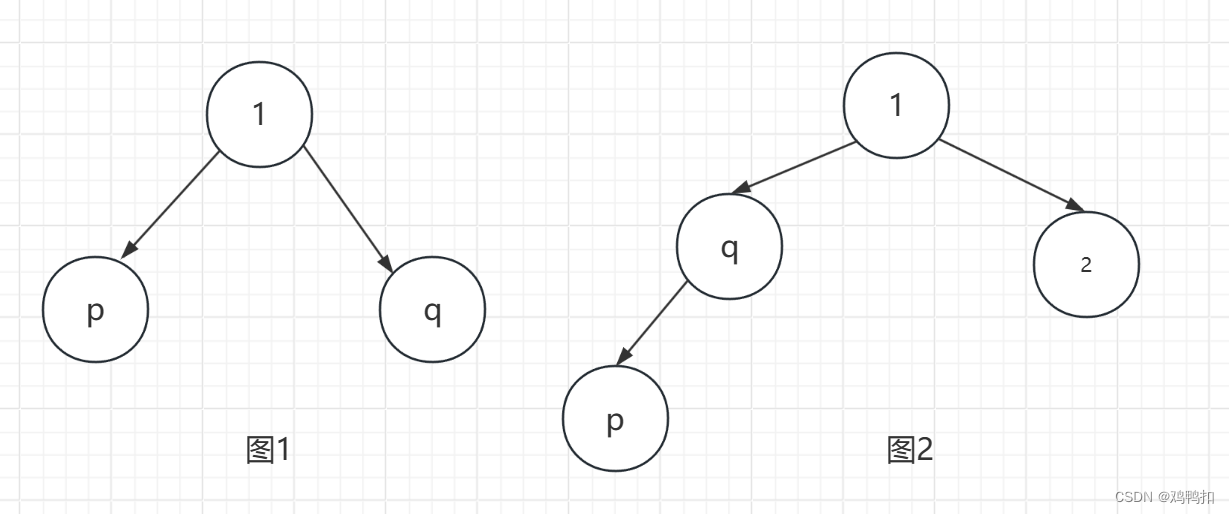
我们可以分析p和q的最近公共祖先的情况，其实总共就两种。

p和q其中有一方是对方的最近公共祖先。最简单的情况如图2。
p和q的最近公共祖先是第三个节点。最简单的情况如图1。

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==null||root==p||root==q) return root;//意味着返回的子树中如果有p或者q，那么才会返回p或者q//如果没有p或者q，那么只会返回空TreeNode left = lowestCommonAncestor(root.left, p, q);TreeNode right = lowestCommonAncestor(root.right, p, q);if(left!=null&&right!=null) return root;//如果左节点和右节点都不为空，说明左子树有p或q其中之一。右子树有p或q其中之一。那么此时就应该返回它俩的父节点return left!=null?left:right;//如果左节点或右节点中有一个为空。那么返回不空的那一个。如果两个都为空，那么返回空节点。}

这部分有点抽象，不好讲，可以去看b站左程云的视频p6：https://www.bilibili.com/video/BV13g41157hK
最终效率是6ms，击败65.96%使用 Java 的用户

寻找后继结点

二叉树的结构包含了父节点指针。头节点的父节点指针指向空。
现在只给某个存在于二叉树的节点node，返回node的节点。
且node和其后继结点之间的路径长度为k的话，时间复杂度为O(k)
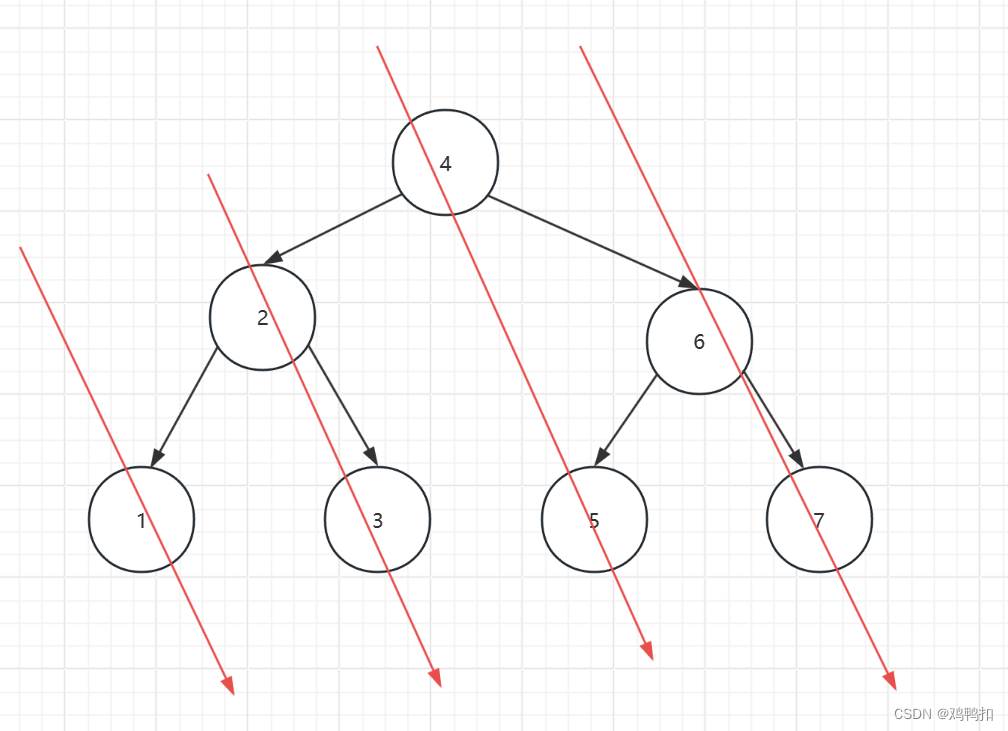
在这里插入图片描述
由图可知，一颗树的中序遍历的顺序是从左上到右下的。那么一个节点的中序后继节点只会分为两种情况。第一，其中序后继和节点本身在一条线上，如节点2和节点3，节点4和节点5。那么也就是说我们该从这个节点出发，找节点的右子树的最左节点。
第二，其中序后继和节点本身不在一条线上，如节点5和节点6.那么也就是说我们该从这个节点出发，找节点的父树的最右节点。
而且注意，因为中序遍历是从左上到右下，所以应该优先去找节点的右子树的最左节点。
综合一句话就是，找这个节点的右子树的最左节点或者父树的最右节点。

第一版（二叉树结构包含父节点指针的）

public Node inorderSuccessor(Node node){if(node==null) return null;if(node.right!=null){Node cur = node.right;while(cur.left!=null){cur = cur.left;}return cur;}else{Node cur = node;Node curFather = node.parent;while(curFather!=null&&curFather.left!=cur){cur = cur.parent;curFather = cur.parent;}return curFather;}}

第二版（二叉树结构不包含父节点指针的）

class Solution {public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {if(root==null) return null;if(p.right!=null){//存在右子树TreeNode cur = p.right;while(cur.left!=null){cur = cur.left;}return cur;}else{//去找左父树HashMap<TreeNode,TreeNode> fatherMap = new HashMap<>();fatherMap.put(root, root);findFather(root, fatherMap);TreeNode cur = p;//6TreeNode curFather = fatherMap.get(p);//5while(curFather.left!=cur){if(cur!=root){cur = fatherMap.get(cur);//5curFather = fatherMap.get(cur);}else{curFather=null;break;}}return curFather;}}public void findFather(TreeNode root,HashMap<TreeNode,TreeNode> fatherMap){if(root==null) return;fatherMap.put(root.left, root);fatherMap.put(root.right, root);findFather(root.left, fatherMap);findFather(root.right, fatherMap);}
}

注意点

注意第一版代码和第二版代码的while循环不太一样。

//第一版的while循环
Node cur = node;
Node curFather = node.parent;while(curFather!=null&&curFather.left!=cur){cur = cur.parent;curFather = cur.parent;}return curFather;//第二版的while循环TreeNode cur = p;TreeNode curFather = fatherMap.get(p);while(curFather.left!=cur){if(cur!=root){cur = fatherMap.get(cur);curFather = fatherMap.get(cur);}else{curFather=null;break;}}return curFather;

因为第一版代码直接包含了父节点指针，所以如果对于如下情况，求6的后继结点，实际上是不存在。
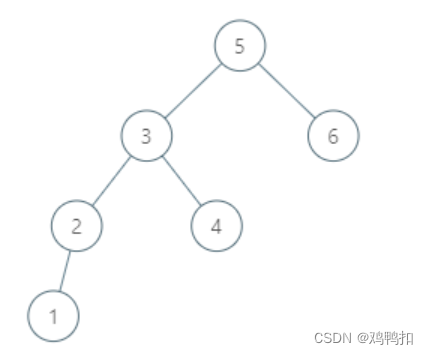
在这里插入图片描述
那么其curFather是可以直接遍历到5的父节点，空节点的
但是如果第二版代码也改成了

TreeNode cur = p;//6
TreeNode curFather = fatherMap.get(p);//5
while(curFather!=null&&curFather.left!=cur){cur = fatherMap.get(cur);//5curFather = fatherMap.get(cur);
}
return curFather;

因为HashMap中是无法存储空节点的，就会导致curFather是遍历不到5的父节点，也就是空节点，从而超出时间限制。

二叉树的序列化和反序列化

就是内存里的一颗树如何变成唯一的字符串形式，又如何从字符串形式变成树的过程。
这里的话以先序遍历来做序列化，遇到空节点就用“#”代替，每个节点之后都以“_”作为结尾。

注意因为保存了空节点的信息，所以只需要先序遍历本身就能确定树的唯一结构。
如果没有保存空节点的信息，那么就需要先序遍历+中序遍历才能确定树的唯一结构。

public class Codec {public String serialize(TreeNode root) {if(root==null) return "#_";String res = root.val+"_";res+=serialize(root.left);res+=serialize(root.right);return res;}// Decodes your encoded data to tree.public TreeNode deserialize(String data) {String[] values = data.split("_");Queue<String> queue = new LinkedList<>();int size = values.length;for(int i=0;i<size;i++){queue.add(values[i]);}return recodeByPreOrder(queue);}public TreeNode recodeByPreOrder(Queue<String> queue){String value = queue.poll();if(value.equals("#")) return null;TreeNode head = new TreeNode(Integer.valueOf(value));head.left = recodeByPreOrder(queue);head.right = recodeByPreOrder(queue);return head;}
}

折纸问题

把纸条竖着放在桌⼦上，然后从纸条的下边向上方对折，压出折痕后再展开。此时有1条折痕，突起的方向指向纸条的背面，这条折痕叫做“下”折痕；突起的⽅向指向纸条正面的折痕叫做“上”折痕。如果每次都从下边向上方对折，对折N次。请从上到下计算出所有折痕的方向，且时间复杂度和空间复杂度就为O(N)

实际上就是满二叉树的中序遍历。

    //i是当前递归到的层数，N是一共的层数，down==true意味着凹，否则为凸public static void printProcess(int i,int N,boolean down){if(i>N) return;printProcess(i+1,N,true);System.out.println(down?"凹":"凸");printProcess(i+1,N,false);}