本文主要是介绍现代控制理论(机器人方向)考核要求与Matlab(Octave)简明教程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
课程全部资料请查阅课程分类:https://blog.csdn.net/zhangrelay/article/category/6161998
现代控制理论成绩构成为如下四个部分:
总成绩根据平时成绩(包括考勤、作业、课堂测试等占30%)、编程考核30%、创新实践报告10%、期末考试(占30%)综合评定。期末考试形式采用闭卷笔试。
创新实践报告模版:https://share.weiyun.com/5tHl9I6
Octave Online(Matlab):https://octave-online.net/
编程示例:https://blog.csdn.net/ZhangRelay/article/details/51615389

Matlab简明教程(对应教材):
可以使用电脑系统Windows/MacOS/Linux,也可以使用手机系统Android/ios等实现。
>> connector on
首次运行 MATLAB Connector 时,必须指定密码。
请输入在设备上设置 MATLAB Mobile 时所用的同一密码。
Password: *************
DNS 名称:
IP 地址: 192.168.x.xxx
使用此链接可测试 MATLAB Connector:
http://192.168.x.xxx:31415/
如果测试成功,但 MATLAB Mobile 无法连接,
可能是因为您的计算机有多个 IP 地址。要确定
正确的地址,请参阅确定计算机的 DNS 名称或 IP 地址。




倒立摆案例:
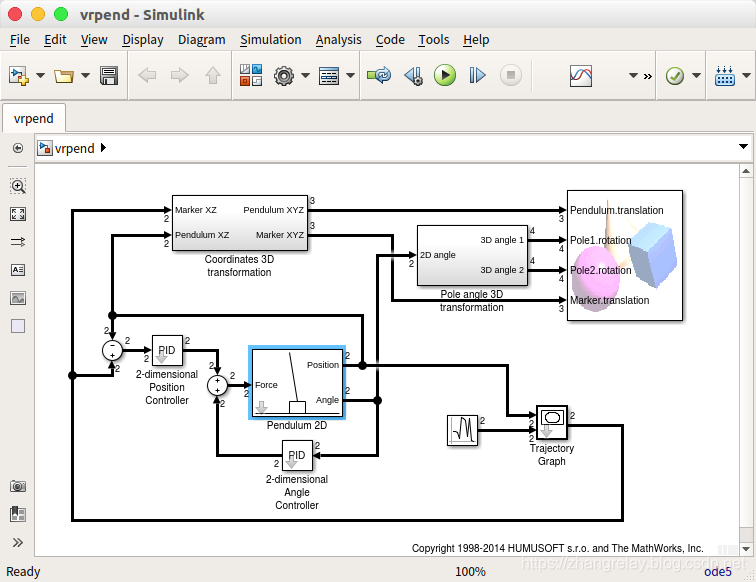
A=[ 0 1 0 0; 0 0 0 0;0 0 0 1; 0 0 29.4 0]
B=[0 ; 1 ; 0 ;3 ]
C=[1 0 0 0; 0 0 1 0]
D=[0 ; 0]syms t
eAt=expm(A*t)ctrb(A,B)rank(ctrb(A,B))
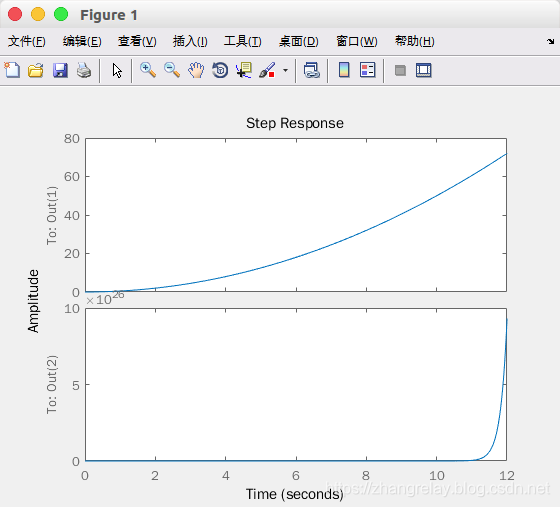
rank(obsv(A,C))step(A, B ,C ,D)
flag=0;
[z,p,k]=ss2zp(A,B,C,D,1);
disp('系统零点,极点和增益为:');
z
p
k
n=length(A);
for ii=1:nif real(p(ii))>0flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end% Q=eye(4,4);
% P=lyap(A,Q);
% flag=0;
% n=length(A);
% for i=1:n
% det(P(1:i,1:i))
% if(det(P(1:i,1:i))<=0)
% flag=1;
% end
% end
% if flag==1
% disp('系统不稳定');
% else
% disp('系统稳定');
% endP=[-10 -10 -2-2*sqrt(3)*i -2+2*sqrt(3)*i]
K=acker(A,B,P)A =0 1.0000 0 00 0 0 00 0 0 1.00000 0 29.4000 0B =0103C =1 0 0 00 0 1 0D =00eAt =[ 1, t, 0, 0]
[ 0, 1, 0, 0]
[ 0, 0, exp(-(7*3^(1/2)*5^(1/2)*t)/5)/2 + exp((7*3^(1/2)*5^(1/2)*t)/5)/2, (3^(1/2)*5^(1/2)*exp((7*3^(1/2)*5^(1/2)*t)/5))/42 - (3^(1/2)*5^(1/2)*exp(-(7*3^(1/2)*5^(1/2)*t)/5))/42]
[ 0, 0, (7*3^(1/2)*5^(1/2)*exp((7*3^(1/2)*5^(1/2)*t)/5))/10 - (7*3^(1/2)*5^(1/2)*exp(-(7*3^(1/2)*5^(1/2)*t)/5))/10, exp(-(7*3^(1/2)*5^(1/2)*t)/5)/2 + exp((7*3^(1/2)*5^(1/2)*t)/5)/2]ans =0 1.0000 0 01.0000 0 0 00 3.0000 0 88.20003.0000 0 88.2000 0ans =4ans =4系统零点,极点和增益为:z =5.4222 0.0000-5.4222 -0.0000p =5.4222-5.422200k =1.00003.0000系统不稳定P =-10.0000 + 0.0000i -10.0000 + 0.0000i -2.0000 - 3.4641i -2.0000 + 3.4641iK =-54.4218 -24.4898 93.2739 16.1633课后习题参考,编程示例不再重复列出。
第一章:状态空间表达式
num为传递函数分子参数,den为传递函数分母参数,tf为传递函数,ss为状态空间,
tf2ss传递函数转状态空间,ss2tf状态空间转传递函数。
掌握系统框图、模拟结构图、状态方程组、状态空间表达式(不唯一)、传递函数等。
% 1.6
num=[6];
den=[1 6 41 7];
[A B C D]=tf2ss(num,den)%1.7
num=[360 440];
den=[1 28 196 740];
[A B C D]=tf2ss(num,den)%1.8%1.9
A=[0 1 -1; -6 -11 6; -6 -11 5];
[P J]=eig(A)
inv(P)*[0;0;1]
[1 0 0]*P%1.10
[T J]=jordan(A)
inv(T)*[0;0;1]
[1 0 0]*T%1.11
A=[0 1 0; 0 0 1; 2 3 0];
[T J]=jordan(A)
%[P J]=eig(A)第二章:表达式的解
step求解阶跃,plot画图。
%2.1 2.2 2.4 2.6
syms t
A=[0 1; -2 -3]
eAt=expm(A*t)%2.3 2.7
syms t
A=[0 1 0; 0 0 1; 2 -5 4]
eAt=expm(A*t)%2.8
syms t
A=[0 1; -2 -3]
B=[0;1]
x0=[0;0]
eAt=expm(A*t)
xt=eAt*x0+inv(A)*(eAt-1)*B*1修订:
%2.8
syms t
A=[0 1; -2 -3]
B=[0;1]
x0=[0;0]
eAt=expm(A*t)
xt=eAt*x0+int(eAt*B*1,t)
%xt=eAt*x0+inv(A)*(eAt-1)*B*1%xt2.6
syms t
A=[0 1; 0 0]
B=[0;1]
C=[1 0]
x0=[1;1]
eAt=expm(A*t)
xt=eAt*x0+int(eAt*B*1,t)
%xt=eAt*x0+inv(A)*(eAt-1)*B*1
yt=C*xt第三章:能控性和能观性
%3.2
A=[-4 5;1 0]
B=[-5;1]
[T,J]=jordan(A)
inv(T)*B%3.5
M=[B, A*B]
rank(M)%3.8
A=[1 2 1; 0 1 0; 1 0 3]
B=[1 0; 0 1; 0 0]
M=[B A*B A*A*B]
rank(M)第四章:稳定性和李雅普诺夫法
%4-1
A=[-1 0; 0 1];
B=[1;1];
C=[1 0];
D=[0];
flag=0;
[z,p,k]=ss2zp(A,B,C,D,1);
disp('系统零点,极点和增益为:');
z
p
k
n=length(A);
for i=1:nif real(p(i))>0flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end%4-5
A=[0 1; -1 -1];
Q=eye(2,2);
P=lyap(A,Q);
flag=0;
n=length(A);
for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end%4-6
A=[0 1; -1 0];
Q=eye(2,2);
P=lyap(A,Q);
flag=0;
n=length(A);
for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end%4-8
A=[1 1; -1 1];
Q=eye(2,2);
P=lyap(A,Q);
flag=0;
n=length(A);
for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end%4-9
A=[0 1; -2 -3];
Q=eye(2,2);
P=lyap(A,Q);
flag=0;
n=length(A);
for i=1:ndet(P(1:i,1:i))if(det(P(1:i,1:i))<=0)flag=1;end
end
if flag==1disp('系统不稳定');
elsedisp('系统稳定');
end第五章:线性定常系统综合
%5-2
A=[0 1 0;0 0 1;0 -2 -3];
B=[0;0;1];
P=[-2 -1+1i -1-1i];
M=[B,A*B,A*A*B];
n=length(A);
rank(M)
if rank(M)==ndisp('系统可控')disp('状态反馈')K=acker(A,B,P)
elsedisp('系统不可控')[Ac,Bc,Cc,T,K]=ctrbf(A,B,C)
end
Ac=A-B*K
disp('配置后极点')
eig(Ac)第六章:最优控制
-未完待续-
这篇关于现代控制理论(机器人方向)考核要求与Matlab(Octave)简明教程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







