机器学习---HMM前向、后向和维特比算法的计算

2024-02-16 14:36
文章标签 算法 学习 计算 机器 前向 hmm 维特

本文主要是介绍机器学习---HMM前向、后向和维特比算法的计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. HMM

import numpy as np# In[15]:class HiddenMarkov:def forward(self, Q, V, A, B, O, PI):  # 使用前向算法N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小alphas = np.zeros((N, M))  # alpha值T = M  # 有几个时刻，有几个观测序列，就有几个时刻for t in range(T):  # 遍历每一时刻，算出alpha值indexOfO = V.index(O[t])  # 找出序列对应的索引for i in range(N):if t == 0:  # 计算初值alphas[i][t] = PI[t][i] * B[i][indexOfO]print('alpha1(%d)=p%db%db(o1)=%f' % (i, i, i, alphas[i][t]))else:alphas[i][t] = np.dot([alpha[t - 1] for alpha in alphas], [a[i] for a in A]) * B[i][indexOfO]  # 递推（）print('alpha%d(%d)=[sigma alpha%d(i)ai%d]b%d(o%d)=%f' % (t, i, t - 1, i, i, t, alphas[i][t]))# print(alphas)P = np.sum([alpha[M - 1] for alpha in alphas])  # 求和终止# alpha11 = pi[0][0] * B[0][0]    #代表a1(1)# alpha12 = pi[0][1] * B[1][0]    #代表a1(2)# alpha13 = pi[0][2] * B[2][0]   #代表a1(3)print(P)def backward(self, Q, V, A, B, O, PI):  # 后向算法N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小betas = np.ones((N, M))  # betafor i in range(N):print('beta%d(%d)=1' % (M, i))for t in range(M - 2, -1, -1):indexOfO = V.index(O[t + 1])  # 找出序列对应的索引for i in range(N):betas[i][t] = np.dot(np.multiply(A[i], [b[indexOfO] for b in B]), [beta[t + 1] for beta in betas])realT = t + 1realI = i + 1print('beta%d(%d)=[sigma a%djbj(o%d)]beta%d(j)=(' % (realT, realI, realI, realT + 1, realT + 1),end='')for j in range(N):print("%.2f*%.2f*%.2f+" % (A[i][j], B[j][indexOfO], betas[j][t + 1]), end='')print("0)=%.3f" % betas[i][t])# print(betas)indexOfO = V.index(O[0])P = np.dot(np.multiply(PI, [b[indexOfO] for b in B]), [beta[0] for beta in betas])print("P(O|lambda)=", end="")for i in range(N):print("%.1f*%.1f*%.5f+" % (PI[0][i], B[i][indexOfO], betas[i][0]), end="")print("0=%f" % P)def viterbi(self, Q, V, A, B, O, PI):N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小deltas = np.zeros((N, M))psis = np.zeros((N, M))I = np.zeros((1, M))for t in range(M):realT = t+1indexOfO = V.index(O[t])  # 找出序列对应的索引for i in range(N):realI = i+1if t == 0:deltas[i][t] = PI[0][i] * B[i][indexOfO]psis[i][t] = 0print('delta1(%d)=pi%d * b%d(o1)=%.2f * %.2f=%.2f'%(realI, realI, realI, PI[0][i], B[i][indexOfO], deltas[i][t]))print('psis1(%d)=0' % (realI))else:deltas[i][t] = np.max(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])) * B[i][indexOfO]print('delta%d(%d)=max[delta%d(j)aj%d]b%d(o%d)=%.2f*%.2f=%.5f'%(realT, realI, realT-1, realI, realI, realT, np.max(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])), B[i][indexOfO], deltas[i][t]))psis[i][t] = np.argmax(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A]))print('psis%d(%d)=argmax[delta%d(j)aj%d]=%d' % (realT, realI, realT-1, realI, psis[i][t]))print(deltas)print(psis)I[0][M-1] = np.argmax([delta[M-1] for delta in deltas])print('i%d=argmax[deltaT(i)]=%d' % (M, I[0][M-1]+1))for t in range(M-2, -1, -1):I[0][t] = psis[int(I[0][t+1])][t+1]print('i%d=psis%d(i%d)=%d' % (t+1, t+2, t+2, I[0][t]+1))print(I)if __name__ == '__main__':Q = [1, 2, 3]V = ['红', '白']A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]# O = ['红', '白', '红', '红', '白', '红', '白', '白']O = ['红', '白', '红', '白']    #例子PI = [[0.2, 0.4, 0.4]]HMM = HiddenMarkov()
#    HMM.forward(Q, V, A, B, O, PI)HMM.backward(Q, V, A, B, O, PI)
#     HMM.viterbi(Q, V, A, B, O, PI)

隐马尔可夫模型是一个统计模型，用于描述由隐藏的状态序列和对应的观测序列组成的系统。在这

个模型中，隐藏的状态是无法直接观测到的，而只能通过观测序列来进行推断。

前向算法（Forward Algorithm）:前向算法用于计算在给定观测序列下每个时间步长处于特定状态

的概率。前向算法利用动态规划的思想，通过递推计算每个时间步的前向概率。前向概率

（alpha）的计算公式为：alpha[t][j] = sum(alpha[t-1][i] * A[i][j] * B[j][O[t]]) for i in range(N)

其中，alpha[t][j]表示在时间步t处于状态j的概率，A[i][j]表示从状态i转移到状态j的概率，B[j]

[O[t]]表示在状态j下观测到序列中的第t个观测的概率。

后向算法（Backward Algorithm）:后向算法用于计算在给定观测序列下每个时间步从特定状态开始

的概率。后向算法同样利用动态规划的思想，通过递推计算每个时间步的后向概率。后向概率

（beta）的计算公式为： beta[t][i] = sum(A[i][j] * B[j][O[t+1]] * beta[t+1][j]) for j in range(N)，其

中，beta[t][i]表示在时间步t从状态i开始的概率，A[i][j]表示从状态i转移到状态j的概率，B[j][O[t+1]]

表示在状态j下观测到序列中的第t+1个观测的概率，beta[t+1][j]表示在时间步t+1处于状态j的概率。

维特比算法（Viterbi Algorithm）:维特比算法用于找到在给定观测序列下最可能的隐藏状态序列。

维特比算法利用动态规划的思想，通过递推计算每个时间步的最大概率和对应的状态。维特比算法

中使用的两个变量是delta和psi，分别表示到达某个状态的最大概率和之前的最优状态。 delta[t][j]

= max(delta[t-1][i] * A[i][j] * B[j][O[t]]) for i in range(N)

psi[t][j] = argmax(delta[t-1][i] * A[i][j]) for i in range(N)

其中，delta[t][j]表示在时间步t到达状态j的最大概率，psi[t][j]表示在时间步t到达状态j时的最优前一

个状态，argmax表示取最大值的索引。

import numpy as np# In[15]:class HiddenMarkov:def forward(self, Q, V, A, B, O, PI):  # 使用前向算法N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小alphas = np.zeros((N, M))  # alpha值T = M  # 有几个时刻，有几个观测序列，就有几个时刻for t in range(T):  # 遍历每一时刻，算出alpha值indexOfO = V.index(O[t])  # 找出序列对应的索引for i in range(N):if t == 0:  # 计算初值alphas[i][t] = PI[t][i] * B[i][indexOfO]print('alpha1(%d)=p%db%db(o1)=%f' % (i, i, i, alphas[i][t]))else:alphas[i][t] = np.dot([alpha[t - 1] for alpha in alphas], [a[i] for a in A]) * B[i][indexOfO]  # 递推（）print('alpha%d(%d)=[sigma alpha%d(i)ai%d]b%d(o%d)=%f' % (t, i, t - 1, i, i, t, alphas[i][t]))# print(alphas)P = np.sum([alpha[M - 1] for alpha in alphas])  # 求和终止# alpha11 = pi[0][0] * B[0][0]    #代表a1(1)# alpha12 = pi[0][1] * B[1][0]    #代表a1(2)# alpha13 = pi[0][2] * B[2][0]   #代表a1(3)print(P)def backward(self, Q, V, A, B, O, PI):  # 后向算法N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小betas = np.ones((N, M))  # betafor i in range(N):print('beta%d(%d)=1' % (M, i))for t in range(M - 2, -1, -1):indexOfO = V.index(O[t + 1])  # 找出序列对应的索引for i in range(N):betas[i][t] = np.dot(np.multiply(A[i], [b[indexOfO] for b in B]), [beta[t + 1] for beta in betas])realT = t + 1realI = i + 1print('beta%d(%d)=[sigma a%djbj(o%d)]beta%d(j)=(' % (realT, realI, realI, realT + 1, realT + 1),end='')for j in range(N):print("%.2f*%.2f*%.2f+" % (A[i][j], B[j][indexOfO], betas[j][t + 1]), end='')print("0)=%.3f" % betas[i][t])# print(betas)indexOfO = V.index(O[0])P = np.dot(np.multiply(PI, [b[indexOfO] for b in B]), [beta[0] for beta in betas])print("P(O|lambda)=", end="")for i in range(N):print("%.1f*%.1f*%.5f+" % (PI[0][i], B[i][indexOfO], betas[i][0]), end="")print("0=%f" % P)def viterbi(self, Q, V, A, B, O, PI):N = len(Q)  # 状态序列的大小M = len(O)  # 观测序列的大小deltas = np.zeros((N, M))psis = np.zeros((N, M))I = np.zeros((1, M))for t in range(M):realT = t+1indexOfO = V.index(O[t])  # 找出序列对应的索引for i in range(N):realI = i+1if t == 0:deltas[i][t] = PI[0][i] * B[i][indexOfO]psis[i][t] = 0print('delta1(%d)=pi%d * b%d(o1)=%.2f * %.2f=%.2f'%(realI, realI, realI, PI[0][i], B[i][indexOfO], deltas[i][t]))print('psis1(%d)=0' % (realI))else:deltas[i][t] = np.max(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])) * B[i][indexOfO]print('delta%d(%d)=max[delta%d(j)aj%d]b%d(o%d)=%.2f*%.2f=%.5f'%(realT, realI, realT-1, realI, realI, realT, np.max(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A])), B[i][indexOfO], deltas[i][t]))psis[i][t] = np.argmax(np.multiply([delta[t-1] for delta in deltas], [a[i] for a in A]))print('psis%d(%d)=argmax[delta%d(j)aj%d]=%d' % (realT, realI, realT-1, realI, psis[i][t]))print(deltas)print(psis)I[0][M-1] = np.argmax([delta[M-1] for delta in deltas])print('i%d=argmax[deltaT(i)]=%d' % (M, I[0][M-1]+1))for t in range(M-2, -1, -1):I[0][t] = psis[int(I[0][t+1])][t+1]print('i%d=psis%d(i%d)=%d' % (t+1, t+2, t+2, I[0][t]+1))print(I)if __name__ == '__main__':Q = [1, 2, 3]V = ['红', '白']A = [[0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]]B = [[0.5, 0.5], [0.4, 0.6], [0.7, 0.3]]# O = ['红', '白', '红', '红', '白', '红', '白', '白']O = ['红', '白', '红', '白']    #例子PI = [[0.2, 0.4, 0.4]]HMM = HiddenMarkov()
#    HMM.forward(Q, V, A, B, O, PI)
#    HMM.backward(Q, V, A, B, O, PI)HMM.viterbi(Q, V, A, B, O, PI)

前向算法（Forward Algorithm）：前向算法用于计算给定观测序列下每个时刻的前向概率

（alpha），表示在当前时刻观测到特定状态的概率。通过递推计算，利用前一时刻的前向概率和

状态转移概率、发射概率来计算当前时刻的前向概率。数学公式：alpha[i][t] = PI[t][i] * B[i]

[indexOfO]，其中alpha[i][t]表示在时刻t处于状态i的前向概率，PI[t][i]表示初始状态概率，B[i]

[indexOfO]表示在状态i观测到观测序列的概率。

后向算法（Backward Algorithm）：后向算法用于计算给定观测序列下每个时刻的后向概率

（beta），表示从当前时刻开始，在未来时刻观测到特定状态的概率。通过递推计算，利用后一时

刻的后向概率和状态转移概率、发射概率来计算当前时刻的后向概率。数学公式：beta[i][t] = Σ(A[i]

[j] * B[j][indexOfO] * beta[j][t+1])，其中beta[i][t]表示在时刻t处于状态i的后向概率，A[i][j]表示状态i

转移到状态j的概率，B[j][indexOfO]表示在状态j观测到观测序列的概率。

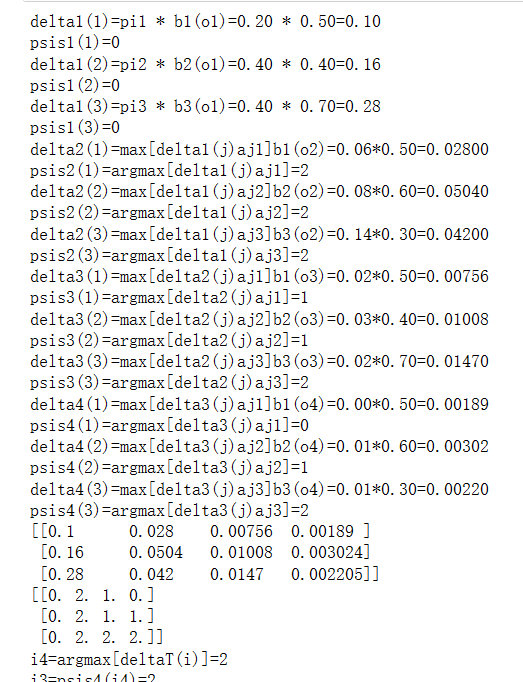
维特比算法（Viterbi Algorithm）：维特比算法用于找到给定观测序列下最可能的隐藏状态序列，

即根据观测序列推断出最可能的隐藏状态路径。通过动态规划的方式，利用状态转移概率、发射概

率和初始状态概率，计算每个时刻每个状态的最大概率值和对应的前一个状态。数学公式：delta[i]

[t] = max(delta[t-1][j] * A[j][i]) * B[i][indexOfO]，其中delta[i][t]表示在时刻t处于状态i的最大概率值，

A[j][i]表示状态j转移到状态i的概率，B[i][indexOfO]表示在状态i观测到观测序列的概率。

这篇关于机器学习---HMM前向、后向和维特比算法的计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/714821。

相关文章

HarmonyOS学习(七)——UI（五）常用布局总结

HarmonyOS学习(七)——UI（五）常用布局总结

自适应布局 1.1、线性布局（LinearLayout） 通过线性容器Row和Column实现线性布局。Column容器内的子组件按照垂直方向排列，Row组件中的子组件按照水平方向排列。 属性说明space通过space参数设置主轴上子组件的间距，达到各子组件在排列上的等间距效果alignItems设置子组件在交叉轴上的对齐方式，且在各类尺寸屏幕上表现一致，其中交叉轴为垂直时，取值为Vert
阅读更多...
Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

Ilya-AI分享的他在OpenAI学习到的15个提示工程技巧

Ilya（不是本人，claude AI）在社交媒体上分享了他在OpenAI学习到的15个Prompt撰写技巧。 以下是详细的内容： 提示精确化:在编写提示时,力求表达清晰准确。清楚地阐述任务需求和概念定义至关重要。例:不用"分析文本",而用"判断这段话的情感倾向:积极、消极还是中性"。 快速迭代:善于快速连续调整提示。熟练的提示工程师能够灵活地进行多轮优化。例:从"总结文章"到"用
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
【前端学习】AntV G6-08 深入图形与图形分组、自定义节点、节点动画（下）

【前端学习】AntV G6-08 深入图形与图形分组、自定义节点、节点动画（下）

【课程链接】 AntV G6：深入图形与图形分组、自定义节点、节点动画（下）_哔哩哔哩_bilibili 本章十吾老师讲解了一个复杂的自定义节点中，应该怎样去计算和绘制图形，如何给一个图形制作不间断的动画，以及在鼠标事件之后产生动画。（有点难，需要好好理解） <!DOCTYPE html><html><head><meta charset="UTF-8"><title>06
阅读更多...
学习hash总结

学习hash总结

2014/1/29/   最近刚开始学hash，名字很陌生，但是hash的思想却很熟悉，以前早就做过此类的题，但是不知道这就是hash思想而已，说白了hash就是一个映射，往往灵活利用数组的下标来实现算法，hash的作用：1、判重；2、统计次数；
阅读更多...
康拓展开（hash算法中会用到）

康拓展开（hash算法中会用到）

康拓展开是一个全排列到一个自然数的双射（也就是某个全排列与某个自然数一一对应） 公式： X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0! 其中,a[i]为整数,并且0<=a[i]<i,1<=i<=n。（a[i]在不同应用中的含义不同）； 典型应用： 计算当前排列在所有由小到大全排列中的顺序，也就是说求当前排列是第
阅读更多...
csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

csu 1446 Problem J Modified LCS （扩展欧几里得算法的简单应用）

这是一道扩展欧几里得算法的简单应用题，这题是在湖南多校训练赛中队友ac的一道题，在比赛之后请教了队友，然后自己把它a掉 这也是自己独自做扩展欧几里得算法的题目 题意：把题意转变下就变成了：求d1*x - d2*y = f2 - f1的解,很明显用exgcd来解 下面介绍一下exgcd的一些知识点：求ax + by = c的解 一、首先求ax + by = gcd(a,b)的解 这个
阅读更多...
综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

综合安防管理平台LntonAIServer视频监控汇聚抖动检测算法优势

LntonAIServer视频质量诊断功能中的抖动检测是一个专门针对视频稳定性进行分析的功能。抖动通常是指视频帧之间的不必要运动，这种运动可能是由于摄像机的移动、传输中的错误或编解码问题导致的。抖动检测对于确保视频内容的平滑性和观看体验至关重要。 优势 1. 提高图像质量 - 清晰度提升：减少抖动，提高图像的清晰度和细节表现力，使得监控画面更加真实可信。 - 细节增强：在低光条件下，抖
阅读更多...
【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

【数据结构】——原来排序算法搞懂这些就行，轻松拿捏

前言：快速排序的实现最重要的是找基准值，下面让我们来了解如何实现找基准值 基准值的注释：在快排的过程中，每一次我们要取一个元素作为枢纽值，以这个数字来将序列划分为两部分。 在此我们采用三数取中法，也就是取左端、中间、右端三个数，然后进行排序，将中间数作为枢纽值。 快速排序实现主框架： //快速排序 void QuickSort(int* arr, int left, int rig
阅读更多...
零基础学习Redis(10) -- zset类型命令使用

零基础学习Redis(10) -- zset类型命令使用

zset是有序集合，内部除了存储元素外，还会存储一个score，存储在zset中的元素会按照score的大小升序排列，不同元素的score可以重复，score相同的元素会按照元素的字典序排列。 1. zset常用命令 1.1 zadd  zadd key [NX | XX] [GT | LT]   [CH] [INCR] score member [score member ...]
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2