本文主要是介绍【阅读笔记】空域保边降噪《Side Window Filtering》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、保边滤波背景
保边滤波器的代表包括双边滤波、引导滤波,但是这类滤波器有一个问题,它们均将待处理的像素点放在了方形滤波窗口的中心。但如果待处理的像素位于图像纹理或者边缘,方形滤波核卷积的处理结果会导致这个边缘变模糊。
基于这个观察,《Side Window Filtering》的作者提出了侧窗滤波,改善边缘被滤波模糊的现象。
2、侧窗滤波原理分析
因为传统方法都使用全窗口回归,也就是把窗的中心位置放在待处理像素的位置。即便是用非线性各向异性加权,仍然无法杜绝沿着图像边缘的法向扩散(可能只是沿着边缘的扩散比较大,而沿着法线的扩散的比较小,比较小也是扩散,这是传统方法不保边的本质原因)。
基于这一分析,把窗口的边缘直接放在待处理像素的位置呢?就切断了可能的法线方向的扩散。这就是这篇文章的核心思想。
有人可能会说:这跟双边滤波的空间加权和灰度值加权非常像啊!但其实还是有本质的区别。我们的方法本质上切断了法向扩散,而不是像之前的保边算法那样仅仅是减少了法向扩散。因此,我们的方法从数学原理上就可以保证保边。而之前的方法本质上是不能保边的。
以上内容摘抄作者发的文章: https://zhuanlan.zhihu.com/p/58326095
3、侧窗滤波算法
常见的滤波算法都是创建方形滤波核,滤波核中心移动到待处理像素进行卷积。比如均值滤波、盒子滤波核和高斯滤波等,滤波处理结果 I i I_{i} Ii是像素的邻域窗口内像素加权求和结果。
I i = ∑ j ∈ Ω i w i j q j I_{i} = \sum_{j\in\Omega_{i}} w_{ij}q_{j} Ii=j∈Ωi∑wijqj
其中, Ω i \Omega_{i} Ωi是像素i的邻域窗口, w i j w_{ij} wij是权重, q q q是输入图像, I I I是滤波输出图像, q j q_{j} qj是邻域像素值
影响滤波结果的是 w w w权重大小、滤波窗口大小形状等。
当像素在边缘,邻域窗口的选择应该在与边缘处在同一侧,不能跨过边缘,提出边缘保持的侧窗滤波算法。将每个目标像素视为潜在边缘,并在其周围生成多个局部窗口(称为侧窗口),每个窗口将目标像素与窗口的一侧或角(而不是中心)对齐。
这篇文章的核心思想:将待处理的像素置于滤波窗口的某个合适的边缘,使得滤波窗口尽可能地位于边缘的一侧,切断了可能的法线方向的扩散
4、侧窗滤波算法实现
具体到一个像素如何选择哪一个方向?横平竖直的子窗口可以利用可分离滤波来加速计算。可以利用重叠的子窗口来减少重复计算。所以,最终的计算量只是原来滤波器的2到3倍。
定义的侧窗(Side Window),包含参数 θ \theta θ、 γ \gamma γ、 ρ \rho ρ,参数 θ \theta θ是窗口与水平线的夹角, γ \gamma γ为窗口半径, ρ \rho ρ作为控制窗口长度的参数且 ρ ∈ { 0 , r } \rho\in \{0,r\} ρ∈{0,r}。
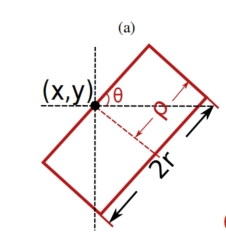
如上图所示,侧窗可以根据参数 θ \theta θ、 γ \gamma γ、 ρ \rho ρ等参数进行调整。
通过改变 θ \theta θ的值我们便能控制窗口的朝向进而决定将窗口的哪一条边放在待处理像素之上。在 γ \gamma γ 固定的情况下,控制 ρ \rho ρ的大小就能控制窗口纵向的长度。
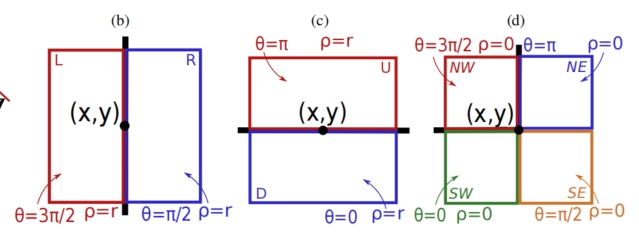
为了保证待处理像素 ( x , y ) (x,y) (x,y) 一定位于窗口边缘或者边角处,直接枚举8个可能的方向。 L 、 R 、 U 、 D 、 N W 、 N E 、 S W 、 S E L、R、U、D、NW、NE、SW、SE L、R、U、D、NW、NE、SW、SE,分别是左、右、上、下、西南、西北、东南、东北。这8类特定的窗口,计算8个窗口的滤波结果,对比原始值最接近的选择那个为最佳的方向。保留边缘意味着我们希望最小化边缘处输入和输出之间的距离,即滤波器输出应与边缘处的输入相同或尽可能接近。
8个方向滤波窗口示意如下图:
ρ = r \rho=r ρ=r时,得到窗口 L 、 R 、 U 、 D L、R、U、D L、R、U、D,当 ρ = 0 \rho=0 ρ=0时,不同 θ \theta θ对应不同侧窗,见下图。
应用滤波核F在不同的侧窗窗口,都得到滤波输出 I i θ , ρ , γ I_{i}^{\theta,\rho,\gamma} Iiθ,ρ,γ,需要满足 θ = k ∗ π / 2 , k ∈ [ 0 , 3 ] \theta=k*\pi/2,k\in[0,3] θ=k∗π/2,k∈[0,3]且 ρ ∈ { 0 , r } \rho\in\{0,r\} ρ∈{0,r}
I i θ , ρ , γ = F ( q i , θ , γ , ρ ) I_{i}^{\theta,\rho,\gamma} =F(q_{i},\theta,\gamma,\rho) Iiθ,ρ,γ=F(qi,θ,γ,ρ)
对于某一像素 (x,y) ,它的侧窗数量可以是无穷多个,我们只选取8个便于计算的特殊角度的窗口,然后再通过比较各个窗口处理的效果最终选出最合适的窗口。
I s w f = arg min ∀ I i θ , ρ , γ ∥ q i − I i θ , ρ , γ ∥ 2 2 I_{swf}=\argmin_{\forall {I_{i}^{\theta,\rho,\gamma}}} \| q_{i} - I_{i}^{\theta,\rho,\gamma}\|_{2}^{2} Iswf=∀Iiθ,ρ,γargmin∥qi−Iiθ,ρ,γ∥22
基于这种side window的思想,我们可以把传统的Box Filter,Gaussian Filter,median Filter,Bilateral Filter,Guided Filter等等都变成Side Window版本。
5、侧窗滤波算法应用
以 box滤波为例,融合侧窗滤波的为 S-box。普通box边缘被模糊,sbox更保边。对不同类型的边缘进行滤波处理,边缘包括以下几种,见图示:
a)gvertical edge (垂直边缘)
d)horizontal edge(水平边缘)
g)diagonal edge(对角边缘)
j)corner(角边缘)
m)ramp edge (斜坡边缘)
p)roof edge(屋顶边缘)
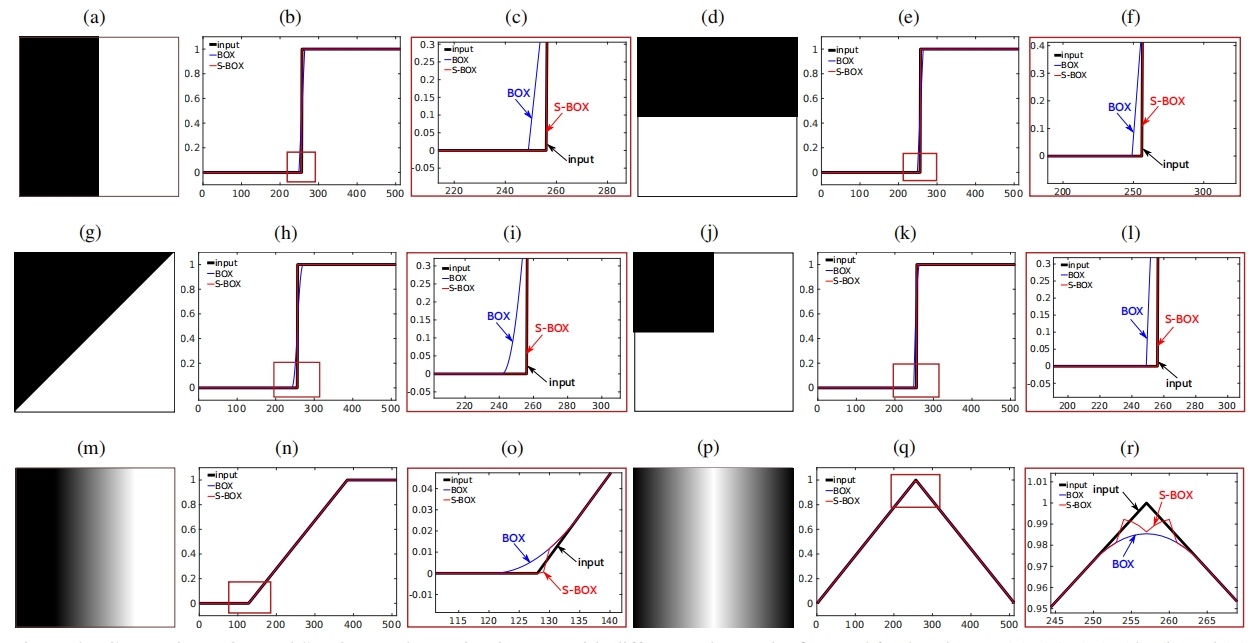
下图时BOX和s-box的计算结果
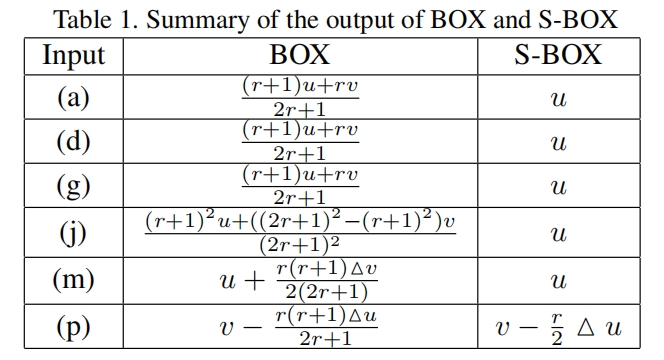
综上,可以得到,不同的侧窗类型可以获得不同的结果。
-
L、NW、SW侧窗口可以保留the edges on the left of the vertical edge(垂直边缘左侧的边缘)。很容易推断出R、NE、SE侧窗口可以保留the edges on the right of the vertical edge(垂直边缘右侧的边缘)。
-
U、NW、NE侧窗口可以保留the edges above the horizontal edge(水平边缘以上的边缘)。同样,很容易证明D、SW、SE侧窗可以保留the edges below the horizontal edge(水平边缘以下的边缘)。
-
NW侧窗口可以保留edges above the diagonal edge and on the corner(对角线边缘上方和拐角上的边缘)。很容易推断出,NE、SW、SE侧窗可以保留diagonal edges and corner with other directions(与其他方向的对角边和角)。
-
L、NW和SW侧窗可以保留ramp edge。
-
侧窗处理roof edge的效果相对较差
6、侧窗滤波算法仿真
仿真实验,将侧窗技术嵌入到高斯滤波器、中值滤波器、双边滤波器和导频滤波器等中,仿真结果见下图,对比改进后效果提升程度。

除此之外还有别的应用场景(比如平滑,HDR应用,结构纹理分解,深度估计,上颜色等),这里就不展示了,融合侧窗滤波思路的效果更好一些,感兴趣的可以看看原文。
参考文章:
https://zhuanlan.zhihu.com/p/58326095
我的个人博客主页,欢迎访问
我的CSDN主页,欢迎访问
我的GitHub主页,欢迎访问
我的知乎主页,欢迎访问
这篇关于【阅读笔记】空域保边降噪《Side Window Filtering》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









