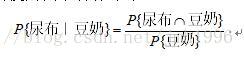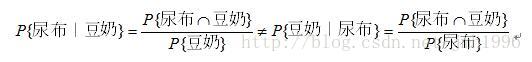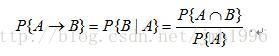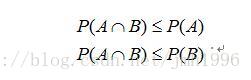Apriori算法--关联分析算法（一）

在实际生产生活我们经常会遇到一些“关联分析”(Association Analyse)的任务。举几个实际例子。

1.人们的购物清单里面的各个商品有没有什么关联呢？就像下面这个购物清单写的那样子，右边是各个顾客所买的东西。

有的时候我们想问，顾客购买商品的时候会不会多个商品组合起来买呢？顾客会不会倾向于豆奶和尿布这两样商品一起买？我们怎么从一份购物清单里面发现这种往往会一起出现的商品组合呢？

2.现在几乎人人都有自己的PC，都会在自己的电脑上安装自己喜欢的软件。现在给出不同工作领域的用户的软件列表，我们能不能发现同种身份的人一般都会按照那些共性的软件呢？这样或许我们就可以给用户推荐他所在领域的受欢迎的软件。

能不能通过计算得到学生群体的共性软件呢？

3.总结疾病的特征。给我们一些疾病的特征，我们如何从这些数据总结出某种疾病的普遍特征呢？比如，给一些患流行性感冒的病人的生理特征数据，我们如何从这些数据发现患流行性感冒的普遍症状呢？

以上这些问题都是关系分析的问题，这些问题希望在数据集中发现其中蕴含的关系，企图发现里面存在的频繁出现的组合（比如学生会经常按照那些软件）或者项与项之间的关系（比如一般安装微信的人也会顺带安装QQ）。发现频繁出现的组合叫做发现频繁项集（frequent item set)，而找出项与项之间的相关关系叫做关联规则学习(association rule analyse)。

#如何量化？
我们如何衡量一个组合是不是频繁出现的呢？频繁是中文含义就是出现的次数多，那么频繁的衡量标准肯定和出现的频数有关。如何计算某个组合的频数？例如：

那么｛豆奶，尿布｝的频数就是3，因为这个组合出现在第2，3，4条样本出现过。

但是，我们也知道频数这个指标是和样本数量的有关的。假如我们规定频数大于5的组合就是频繁的。那这样子假如某个组合在10条随机数据集中的频数为1，这个组合是不频繁的；但是在100条随机数据集中频数为10，该组合变的频繁了。这就会导致频繁性的判断不稳定。因此实际上我们使用频率这个指标。

实际上一个组合A的频率又叫组合A在这个数据集T上的支持度（support degree）,意思就是组合A在数据集T上出现的概率。

那么我们如何定义关联规则可信呢？已知一个人已经买了豆奶，那么他有多大概率也买尿布嘞？这个就要使用到条件概率了。

这个条件概率的直观解释就是：在所有出现豆奶的样本里，有多少个还出现了尿布。如果这个条件概率特别大，那么我们可以认为**“买了 豆奶 一般也会买 尿布 ”**这条规则是可信任的。规则 “买了 豆奶 一般也会买 尿布” 记作：豆奶——>尿布。但是这条关联规则不具备自反性。也就是说 豆奶——>尿布，并不能推出 尿布——>豆奶，本质上是因为他们的条件概率都不同：

直观上的理解也是一样的。比如 人们一般上完厕所就会洗手，规则：上厕所——>洗手 是可信的；但是并不意味着 洗了手就一定是在上厕所，因为也可能是吃了饭再洗手。

同样的，在关联分析中，与某条规则相对应的条件概率也有另外一个名称：置信度。

规则A->B的置信度计算公式为：

有了这两个量化指标，那我们就可以在一个数据集上寻找频繁项集和关联规则啦。
最原始的做法就是，生成所有可能的组合方式，然后我们枚举计算这些所有的组合方式的支持度（频率），那些达到支持度指标的就是我们想到找到的频繁项集啦。这种枚举法当然可以解决问题，但是我们想也想的到这个复杂度特别高！

比如上面购物的例子中基础元素共有6个，这6个元素可以一个一个组合，也可以两个两个组合，也可以三个三个来•••那么这6个基本元素组合起来就一共有：
种可能的组合方式。如此，我们需要计算63种组合出现的频率，每次计算需要遍历整个数据集。emmmmm…这个时间复杂度O(2^N)要GG。那么一个自然的思路就是剪枝。

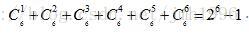
#使用Apriori 原理进行剪枝

Apriori原理特别简单！有一些公理化概率论基础都会轻松理解。

设A,B是两个事件，则

积事件的概率小于等于各个因子的概率。直观的解释就是A和B同时发生的概率当然要小于等于他们单独分别发生的概率。

ok.我们来使用这个性质对上面寻找频繁项集的过程进行剪枝。

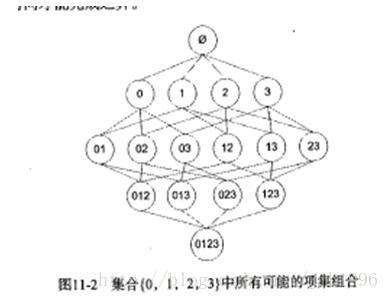
上图显示了基础元素集为｛0，1，2，3｝时，所有可能的组合。这实际显示了一种生成所有组合的层次化的方法：先一一组合，然后再二二组合，再三三组合•••每一层的组合都可以在上一层的基础上进行。具体方法为：

设第i层是所有含i个元素的组合，每个组合都有i+1个不同的元素。现在需要生成所有含i+1个元素的组合。

i+1个元素的组合就是每个组合含有i+1个不同的元素；那么只要在原来第i层的基础上进行两两合并，生成含且只含i+1个元素的组合。

为了让第i层两个组合CA,CB组合后生成只含i+1个元素，需要CA,CB有且只有一个元素不同。否则合并后的组合将不只i个元素。

所以我们可以让所有组合按基础元素升序的方式排列，比较CA,CB前i-1个元素.如果CA和CB的前i-1个元素相同的话，CA和CB就只有第i个元素不同了（如01和02），这样合并后才能只含有i+1个元素。如果CA和CB的前i-1个元素不等，那至少CA与CB会有两个元素不一致（如01 和23 组合生成0123 就包含4个基本元素）。 （此方法存在问题，感谢@weixin_39799208指正）
正确的做法应该是对CA和CB内的各元素做交集，看交集内的元素个数是否为i-1。

现在 我们假设{23}组合的支持度为P({23})，它小于容许的最小支持度p’,即P(23) < p’,此时｛23｝这种组合就是不频繁的了。

由图可知，｛23｝参与了组合｛023｝和｛123｝的生成，那么：

#Apriori的实现代码：

__author__ = 'jmh081701'
import  numpy as npdef loadDataset():return [{1,3,4},{2,3,5},{1,2,3,5},{2,5}]
def createC1(dataset,minsupport=0.6):C1=[]for t in dataset:for s in t:if({s} in C1):continueelse:C1.append({s})C1.sort()return map(frozenset,C1)def scan(dataset,minisupport=0.6,Ck=None):rst=[]cutset=[]supportData={}for c in Ck:for t in dataset:if c.issubset(t):if c in supportData:supportData[c]+=1else:supportData[c]=1lenD=float(len(dataset))for key in supportData:supportData[key]=supportData[key]/lenDif(supportData[key]>=minisupport):rst.append(key)else:cutset.append(key)return rst,supportData,cutsetdef genCj(Ck,k,Cutset={}):#2019年04.10 此实现有问题，应该是取l1,l2交集然后判断交集元素个数是否符合要求。lenCk=len(Ck)Cj=set()for i in  range(lenCk):for j in range(i+1,lenCk):l1=list(Ck[i])[:k-1]l2=list(Ck[j])[:k-1]l1.sort()l2.sort()if(l1==l2):t=Ck[i]|Ck[j]f=0for each in Cutset:if set(each).issubset(t):f=1breakif(f==0):Cj.add(t)return Cjdef apriori(dataset,minisupport=0.6):#from number i layer frequent item set generate i+1 th frequent item set.C1=createC1(dataset)Ck=C1k=1supportData={}CutSet=[]rstC=[]while Ck!=set():rst,support,cutset=scan(dataset,minisupport,Ck)rstC.append([rst])supportData.update(support)CutSet.append(cutset)Cj=genCj(rst,k,CutSet)k+=1Ck=Cjreturn rstC,supportData
data=loadDataset()
rstC,supportData=apriori(data)
print(rstC)
print(supportData)

运行结果：

[[[frozenset({3}), frozenset({2}), frozenset({5})]], [[frozenset({2, 5})]]]
{frozenset({1}): 0.5, frozenset({3}): 0.75, frozenset({4}): 0.25, frozenset({2}): 0.75, frozenset({5}): 0.75, frozenset({2, 3}): 0.5, frozenset({3, 5}): 0.5, frozenset({2, 5}): 0.75}

#代码解释

def loadDataset():return [{1,3,4},{2,3,5},{1,2,3,5},{2,5}]

该函数用于生成数据集。输入数据集是一个list of set.列表里面的每一个元素都是集合。在关联分析中，需要将原始数据转化为这种数据形式。尤其是每个样本的特征向量其实是一个无序的集合。

def createC1(dataset,minsupport=0.6):C1=[]for t in dataset:for s in t:if({s} in C1):continueelse:C1.append({s})C1.sort()return map(frozenset,C1)

该函数遍历整个数据集，将各个基础元素抽离出来。注意最后的map{frozenset,C1}

map(func, seq1[, seq2,…]) 
第一个参数接受一个函数名，后面的参数接受一个或多个可迭代的序列，返回的是一个集合。 Python函数编程中的map()函数是将func作用于seq中的每一个元素，并将所有的调用的结果作为一个list返回。

map(frozenset,C1)其实就是将C1的每一个元素都转化为frozenset类型。这么做是为了让元素组合能够做字典的key.

def scan(dataset,minisupport=0.6,Ck=None):rst=[]cutset=[]supportData={}for c in Ck:for t in dataset:if c.issubset(t):if c in supportData:supportData[c]+=1else:supportData[c]=1lenD=float(len(dataset))for key in supportData:supportData[key]=supportData[key]/lenDif(supportData[key]>=minisupport):rst.append(key)else:cutset.append(key)return rst,supportData,cutset

上述代码在计算各个组合的频率。
对于Ck里面的每一个组合c,遍历整个数据集，看这个c在数据集中出现了多少次。按照定义，c是t的子集说明 c在t出现了。

rst是满足Ck内所有满足最小支持度要求的组合；同时supportData返回了Ck内所有组合的支持度，supportData是一个字典，key是基本元素的组合，而value是这个组合出现的频率。cutset用于返回Ck内那些被剪枝的组合。

def genCj(Ck,k,Cutset={}):lenCk=len(Ck)Cj=set()for i in  range(lenCk):for j in range(i+1,lenCk):l1=list(Ck[i])[:k-1]l2=list(Ck[j])[:k-1]l1.sort()l2.sort()if(l1==l2):t=Ck[i]|Ck[j]f=0for each in Cutset:if set(each).issubset(t):f=1breakif(f==0):Cj.add(t)return Cj

genCj用于输入只含k个元素的若干组合Ck，以及已确定被剪枝的组合列表Cutset,输出含k+1个元素的所有可能的组合Cj。注意要先把前k-1个元素提取出来，然后排序，比较、如果相等后t不含有cutset的元素 再把合并后的加入。

def apriori(dataset,minisupport=0.6):#from number i layer frequent item set generate i+1 th frequent item set.C1=createC1(dataset)Ck=C1k=1supportData={}CutSet=[]rstC=[]while Ck!=set():rst,support,cutset=scan(dataset,minisupport,Ck)rstC.append([rst])supportData.update(support)CutSet.append(cutset)Cj=genCj(rst,k,CutSet)k+=1Ck=Cjreturn rstC,supportData

当第k层一直不空的时候，不断寻找新的组合。

注意：关联分析的输入数据集中，每个样本的特征向量是一个集合，是无序的、确定的、互斥的。