本文主要是介绍算法快学笔记(十六):动态规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 介绍
前文提到,对于背包问题与旅行商问题,计算的复杂度是随着计算数据的增加呈现指数级增长的,贪婪算法算可以处理,但得到的并不是最优解。
动态规划的主要思路是先解决子问题,在逐步解决大问题。本文将通过两个例子介绍动态规划的推算思路。
2. 背包问题
2.1 思路
通过动态规划方法解决背包问题的流程如下:
-
准备一个表格,商品作为Y轴,背包重量作为x轴
-
使用下面的公式算出价格且更新到表格里

-
使用方法2,逐行填充表格,直到将表格填满。
2.2 推算过程
用于推算的数据如下:
- 小偷的背包可以放4KG的物品
- 可偷物品的价格,重量如下:
| 物品 | 重量 | 价值 |
|---|---|---|
| 吉他 | 1kg | 1500 |
| 音响 | 4kg | 3000 |
| 笔记本 | 3kg | 2000 |
| 手机 | 1kg | 2000 |
详细推算过程如下:
- 初始化表格如下
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | ||||
| 音响 | ||||
| 笔记本 | ||||
| 手机 |
- 吉他是第一个商品,且重量只有1kg,则对于不同大小的背包而言都可以放得下,所以第一行的值都为1500
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | ||||
| 笔记本 | ||||
| 手机 |
- 音响是第二个商品,对于1,2,3三个背包都放不下,所以能放的物品价值还是1500,第四个背包可以放下,使前面提到的公式推导一下。
- CELL[1][4]=1500
- 当前价值+剩余空间价值=3000+0(没有剩余的空间,所以剩余价值为0)
通过上面的推算,可知音响这行最后一格的值为3000
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | ||||
| 手机 |
- 看下笔记本,前两个背包都放不下,从第三个开始。第三个背包放完笔记本后价值为2000,且比CELL[2,3]要大,所以该值更新为2000
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | |
| 手机 |
再来看笔记本的最后一格,比较下面的值:
- CELL[2][4]=3000
- 2000(笔记本价格)+1500(剩余空间的最大价值)=3500
由上可得出笔记本第四格的价值应该是3500
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | 3500 |
| 手机 |
- 手机的重量为1kg.且比吉他的价格要贵,所以第一格替换成手机的价格
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | 3500 |
| 手机 | 2000 |
对于第二格,比较下面的值:
- CELL[3][2]=1500
- 2000(笔记本价格)+1500(剩余空间的最大价值,C[3,1])=3500
由上可得出手机第二格的价值应该是3500
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | 3500 |
| 手机 | 2000 | 3500 |
第三格的推算过程与第二格类似,值同样为3500.
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | 3500 |
| 手机 | 2000 | 3500 | 3500 |
对于第四格,比较下面的值:
- CELL[3][4]=3500
- 2000(笔记本价格)+2000(剩余空间的最大价值,C[3,3])=4000
由上可得出手机第四格的价值应该是4000
| * | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 吉他 | 1500 | 1500 | 1500 | 1500 |
| 音响 | 1500 | 1500 | 1500 | 3000 |
| 笔记本 | 1500 | 1500 | 2000 | 3500 |
| 手机 | 2000 | 3500 | 3500 | 4000 |
最终可得知,小偷最多可偷4000元的商品,且偷的商品是手机+笔记本电脑。
2.4 其他注意事项
- 最终的结果和表格中商品的顺序没有关系
- 如果可偷的商品为0.5kg. 则x轴的粒度要为0.5。既0.5->1->1.5->2…
- 选择商品的时候,每个商品都是独立选择的,不存在依赖关系。例如不应该出现选择商品A,则必须(不能)选择B的情况
- 最优解可能会导致最终的背包没有被装满
3. 最长公共子串
最场公共子串求出的是两个字符串都包含的最长子串,例如:对于hish与fish两个单词,ish就是他们的最长公共子串。
3.1 思路
可以用解决背包问题的思路来解决该问题,两个单词分别对应纵/横轴,将公共子串的长度填到方格里,最后所有格子里最大的值就是最大的公共子串的长度,连续从0到最大长度值对应的纵/横轴对应的字母就是最长公共子串。
格子里值的推算公式如下:
if word_a[i] == word_b[j]:cell[i][j] = cell[i-1][j-1] + 1
else:cell[i][j] = 0
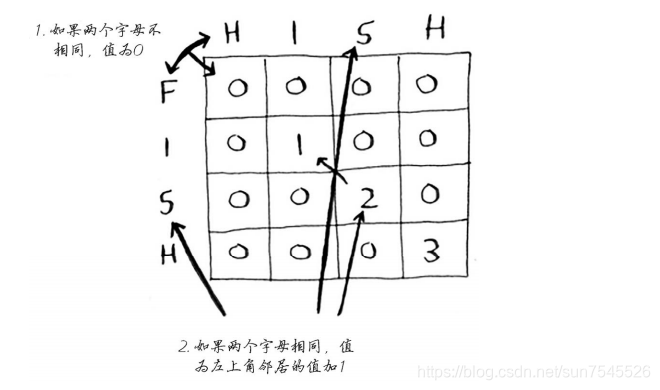
按照上面的公式推算,FISH与HISH的结果如下:
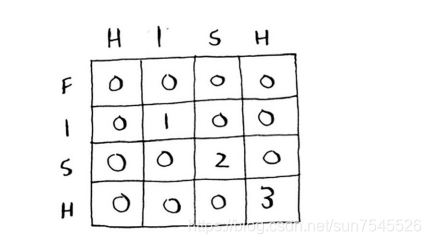
既最大长度为3,对应的子串为ISH.
3.2 最长公共子序列
最长公共子序列:两个单词中都有的序列包含的字母数,最后求得的子序列长度越长,说明两个单词越相似
算法的步骤如下:
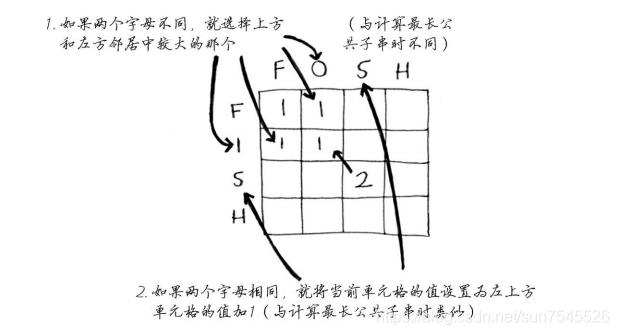
计算FOSH与FISH与FORT两个单词的最长公共子序列的过程与结果如下:
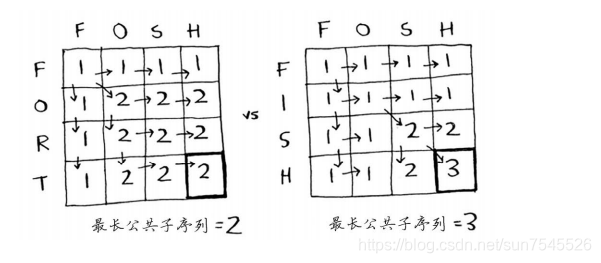
通过上述结果可看出,FISH与FOSH更像一些。
4. 总结
动态规划的实际应用包括如下场景:
-
生物学家根据最长公共序列来确定DNA链的相似性,进而判断度两种动物或疾病有多相似。
-
前面讨论了字符串的相似程度。 编辑距离( levenshtein distance)指出了两个字符串的相
似程度,也是使用动态规划计算得到的。编辑距离算法的用途很多,从拼写检查到判断用户上传的资料是否是盗版,都在其中。 -
Microsoft Word等具有断字功能的应用程序,使用动态规划确定在什么地方断
字以确保行长一致。
这篇关于算法快学笔记(十六):动态规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



