本文主要是介绍算法快学笔记(十五):贪婪算法与NP完全问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 贪婪算法
1.1 算法思路
贪婪算法的思想很简单:每步都采取最优的做法,以教室调度为例进行说明该算法步骤。
假设有以下课表,希望将尽可能多的课程安排在同一个教室:
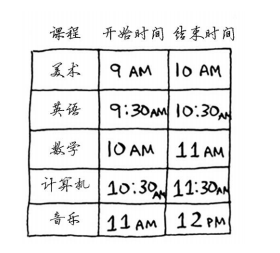
由于不同课的开始与结束时间存在冲突,所以不可能把所有课放在一个教室上。使用贪心算法的解决思路如下:
- 选出结束最早的课,它是上的第一堂课。 此时选择美术课
- 接下来选择第一堂课结束后才开始的课。同样,你选择结束最早的课,这将是要第二堂课。此时选择数学课。
- 重复步骤二,此步得到音乐课
于是使用贪婪算法得到的结果就是:美术-》数学-》音乐。
1.2 例外情况
贪婪算法并不适合所有的场景,例如背包问题。背包问题描述如下:
- 假设一个背包可以放35磅重的东西,你试图通过该背包尽可能装入总价值最高的商品
- 商品的列表如下:
- 音响:3000美元,30磅
- 电脑:2000美元,20磅
- 吉他:1500美元,15磅
按照贪婪算法,每步都选择最优方案的话,则第一步将会选择音响,此时总价值为3000美元,背包还剩5磅的空间,然后其他的物品超过了5磅,所以也不能再进行选择。
如果选择电脑+音响的话,总价值为3500美元,重量刚好符合要求。
总结:当你只需找到一 个能够大致解决问题的算法,此时贪婪算法正好可派上用场,因为它们实现起来很容易,得到的结果又与正确结果相当接近。
2. NP完全问题
对于一些需要较大计算量才能解决的问题可理解为NP完全问题,为了可以更好的理解这个概念,以集合覆盖问题以及旅行商问题对该问题进行说明
2.1 集合覆盖问题(组合问题)
假设你办了个广播节目,要让全美50个州的听众都收听得到。为此,你需要决定在哪些广播台播出(全组合问题)。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。广播电视台的清单如下:
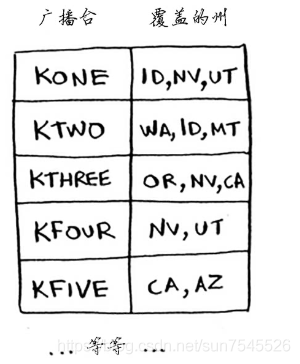
每个广播台可能覆盖多个区域,不同广播台的区域可能重叠,如何找出覆盖全美50个州的最小广播台集合呢?听起来很容易,但其实非常难。具体方法如下。
- 列出每个可能的广播台集合,该问题等价于有n个广播台,则存在多少种组合的可能,组合的推导公式为:
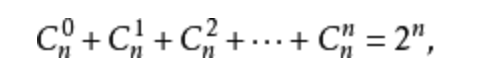
- 从步骤一得列表中选择出可以覆盖50个州得最小集合。
当有100个站点时,就有2的100次方个组合的可能,对于目前的计算机性能而言,该集合的数量将会成为一个计算难题。
2.2 旅行商问题(排列问题)
如果有N个城市需要遍历,期初可以选择的城市有N个,下一步可选择的城市为N-1个,下下步可选择的城市为N-2个…。该问题可转化为数学中的全排列问题,既有N个城市时,有N!种可能。
该问题与集合覆盖问题类似,当N很大时,计算结果需要花费较大的计算资源。
2.3 定义
NP完全问题有以下几个显著的特点:
- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
- 涉及“全排列”与“全组合”的问题通常是NP完全问题。
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
2.4 NP完全问题的解决方案
可以使用近似算法来解决解决该问题,该问题说明请看下节。
3. 近似算法
近似算法(approximation algorithm)是指由于获得精确解需要的时间太长时,可使用近
似算法。判断近似算法优劣的标准如下:
- 速度有多快;
- 得到的近似解与最优解的接近程度。
贪婪算法是近似算法的一个代表,它不仅简单,而且通常运行速度也很快。
这篇关于算法快学笔记(十五):贪婪算法与NP完全问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








