本文主要是介绍片上网络NoC（4）——直连拓扑，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
一、前言
二、直连拓扑
三、总结
一、前言
本文中，我们将继续介绍片上网络中拓扑相关的内容，主要介绍直连拓扑，在此之前，我们已经介绍过了拓扑的指标，这将是继续阅读本文的基础，还没有了解相关内容的读者可以阅读以下文章。
片上网络NoC（3）——拓扑指标
https://blog.csdn.net/apple_53311083/article/details/136106748?spm=1001.2014.3001.5501
二、直连拓扑
直连拓扑指每个终端节点（如单芯片多处理器的一个处理器核或缓存）都配备一个路由器的网络拓扑；所有路由器既是流量的产生与汇入端，又是流量的中转站。到目前为止，大多数片上网络的设计都使用了直连网络，因为将路由器与终端节点放在一起考虑，通常适合芯片这种存在电路面积限制的环境。
我们首先介绍以下3种常见的直连拓扑：ring、mesh和torus。
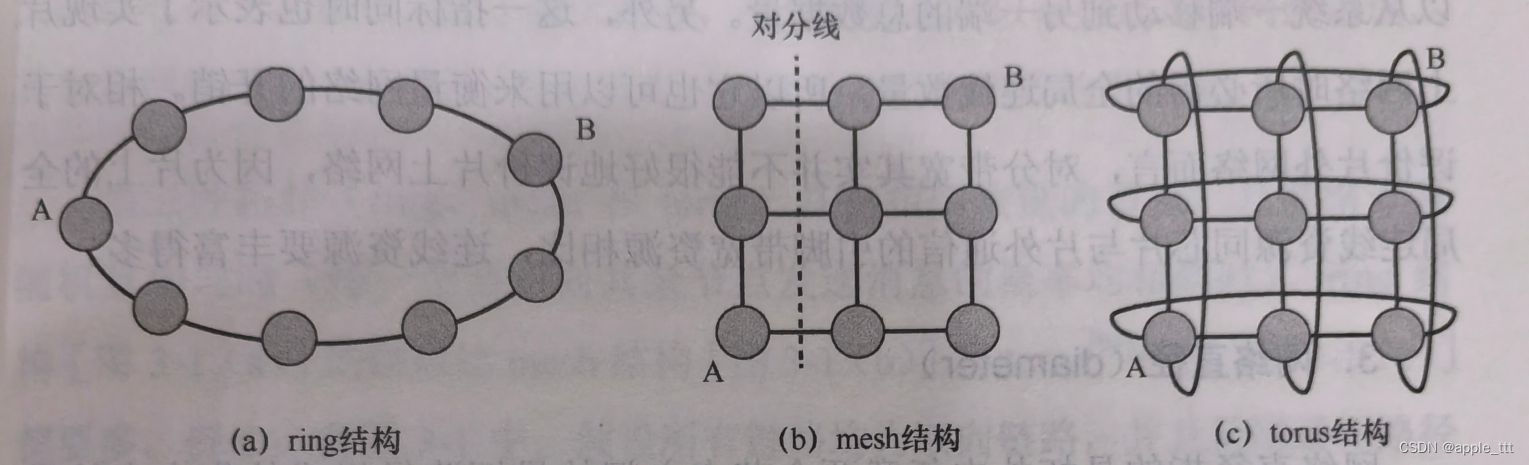
ring结构中的所有节点组成了一个一维的环形；在二维mesh结构（2D mesh）中，节点组成了规则的二维网格，每个节点与其四周的邻近节点相连；而torus结构则是对mesh结构的进一步改进，它通过将网络两侧边缘的对应节点相连，使网格在这一维度上构成了环路。
直连拓扑可以描述为 k-ary n-cube，其中k是每个维度上的节点数，n是维度数。举个例子，4×4的mesh和torus结构可以描述为4-ary 2-cube，它们的维度数都是2，每个维度上的节点数是4，一共有4×4=16个节点；8×8的mesh或者torus结构有64个节点，可以描述为8-ary 2-cube。同理，一个4×4×4的mesh或torus结构有64个节点，可以描述为4-ary 3-cube。这样的描述方法假设每个维度上都具有相同数量的节点，所以网络的节点总数可以表示为。从实际角度讲，绝大多数片上网络使用2D mesh拓扑，以方便在平面基板上进行电路映射，因为更复杂的网络拓扑需要更多的金属布线层。这与部署在片外的网络是不同的，因为片外基板的连接线不受平面的限制，可以是立体的。在每个维度上，k个节点通过通道连接到离它们最近的邻居节点。ring 结构由于可以描述为 k-ary 1-cube，所以也可以将其归为 torus类结构。
对一个torus结构来说，所有的节点都有同样的节点度；但是，对mesh结构来说，网络边缘节点的度比网络中心节点的度要小。torus结构是边缘对称的（mesh结构不是），这个属性可以帮助torus结构更好地平衡各通道的流量。相应地，由于不具备边缘对称性，mesh结构对位于网络中心通道的负载要求比边缘通道高。
接下来，我们用之前提出的一些抽象的度量指标来评估torus和mesh网络。torus网络在每个维度上需要两个通道，整个torus网络需要2n个通道。因此，对一个2D torus网络来说，它的度是4；对一个3D torus网络来说，它的度是6。对mesh网络来说，它的度也是和torus网络相同的，尽管在网络边缘的端口可能不会被使用到。torus 网络的平均最小跳数是通过计算网络中所有可能的节点对之间的最短路径的均值得到的。
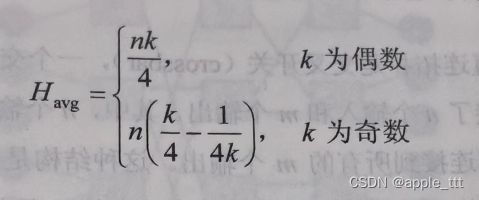
tours网络去除环绕的链路后就是mesh网络。mesh网络的平均最小跳数比tours网络稍大：
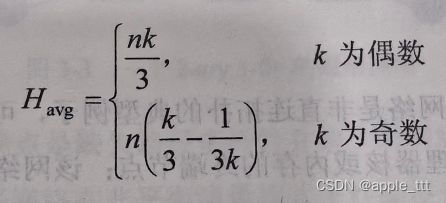
对于均匀随机流量下参数k为偶数的torus网络，其对分切割后两部分之间的最大通道负载是k/8，其将网络最大注入带宽限制在了8/k flit/node/cycle。对mesh来说，最大通道负载将会增大到k/4，因此网络最大注入带宽减小至4/k flit/node/cycle。
和ring网络相比，mesh和torus网络都具有路径多样性。随着网络维度的增加，其路径多样性也会增加。
三、总结
本文介绍了片上网络拓扑中的直接形式，主要以ring、mesh和torus为例，对直连拓扑的各项指标进行了说明。
这篇关于片上网络NoC（4）——直连拓扑的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
