本文主要是介绍剑指offer 66题 part5(25~30题),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
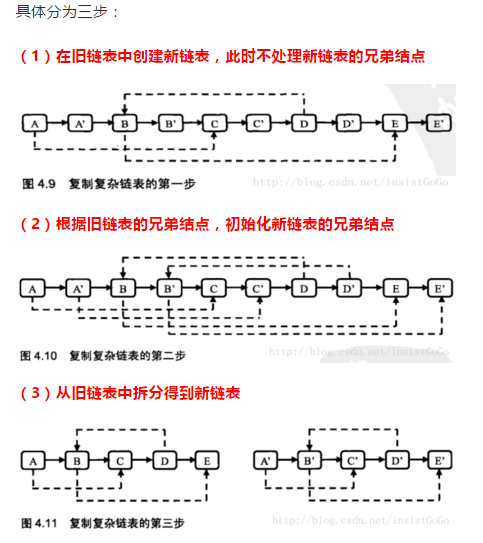
第二十五题:复杂链表的复制
通过看图以及下面代码的注释,就可以很快的看懂啦
/*
struct RandomListNode {int label;struct RandomListNode *next, *random;RandomListNode(int x) :label(x), next(NULL), random(NULL) {}
};
*/
class Solution {
public:RandomListNode* Clone(RandomListNode* pHead){if(!pHead) return NULL;RandomListNode* cur=pHead;while(cur){///本循环是克隆每一个节点RandomListNode* cloneNode=new RandomListNode(cur->label);//下面三行是交换,类似swap的思想RandomListNode* nextNode=cur->next;cur->next=cloneNode;cloneNode->next=nextNode;///移动指针cur=nextNode;}cur=pHead;while(cur){///复制老节点的随机指针给新节点cur->next->random=cur->random?cur->random->next:NULL;cur=cur->next->next;}cur=pHead;RandomListNode* ans=pHead->next;while(cur){///拆分链表RandomListNode* cloneNode=cur->next;cur->next=cloneNode->next;cloneNode->next=cloneNode->next?cloneNode->next->next:NULL;cur=cur->next;}return ans;}
};第二十六题:二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向
题解:
因为二叉搜索树可以看做是有序的,故可以利用其左右儿子当做双向链表的前后指针
然后又发现,其实中序遍历BST就是我们所需要的答案,但是我们是需要转换指针指向的,所以看下面代码,纸上面模拟即可
/*
struct TreeNode {int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};*/
class Solution {
private:TreeNode * leftHead=NULL,* rightHead=NULL;
public:TreeNode* Convert(TreeNode* pRootOfTree){if(!pRootOfTree) return NULL;Convert(pRootOfTree->left);if(!leftHead) leftHead=rightHead=pRootOfTree;else{rightHead->right=pRootOfTree;pRootOfTree->left=rightHead;rightHead=rightHead->right;}Convert(pRootOfTree->right);return leftHead;}
};第二十七题:字符串的排列
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba
题解:
每次两两交换,就能得到新的我们所需要的串
模拟这个思想即可
class Solution {
private:void deal(vector<string> &ans,string str,int p){if(p==(str.size()-1)) ans.push_back(str);for(int i=p;i<str.size();i++){if(i!=p&&str[i]==str[p]) continue;//这里在i!=p的时候才去判断是不是不同的字母swap(str[i],str[p]);//i==p的时候我们也要递归,意思是原样不懂的str也可以作为一个排列deal(ans,str,p+1);swap(str[i],str[p]);//进行两次交换是dfs的常态思想}}
public:vector<string> Permutation(string str) {vector<string>ans;///字符串类型if(str.size()==0) return ans;deal(ans,str,0);sort(ans.begin(),ans.end());return ans;}
};第二十八题:数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0
题解:
超过一半,则必然和其他的数字进行抵消能剩余
class Solution {
public:int MoreThanHalfNum_Solution(vector<int> numbers) {int size=numbers.size(),cnt=1,num=numbers[0];for(int i=1;i<size;i++){if(numbers[i]==num) cnt++;else cnt--;if(!cnt) num=numbers[i],cnt=1;}cnt=0;for(int i=0;i<size;i++)if(num==numbers[i]) cnt++;return cnt*2>size?num:0;}
};第二十九题:最小的k个数
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,
题解:
方法很多:优先队列,堆排序等等各种排序
class Solution {
public:vector<int> GetLeastNumbers_Solution(vector<int> input, int k) {vector<int>ans;if(input.size()<k) return ans;sort(input.begin(),input.end());for(int i=0;i<k;i++)ans.push_back(input[i]);return ans;}
};第三十题:连续子数组的最大和
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住?(子向量的长度至少是1)
题解:
这种题目其实就是dp
简单的dp,鉴于之前搞acm已经很熟悉了就不介绍这种思路了,其实很简单的,纸上模拟一下即可
class Solution {
public:int FindGreatestSumOfSubArray(vector<int> array) {int tmp=0,ans=-0xfffffff,size=array.size();for(int i=0;i<size;i++){tmp+=array[i];if(tmp>ans) ans=tmp;if(tmp<0) tmp=0;}return ans;}
};这篇关于剑指offer 66题 part5(25~30题)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!