[dp] 动态规划学习路线与笔记

本文主要是介绍[dp] 动态规划学习路线与笔记 | 动态规划习题集，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文链接：https://www.yuque.com/cppdev/algo/tyahkd
【学习路线】

对动态规划有一个初步的了解，只看问题引入的部分：什么是动态规划？动态规划的意义是什么？
B站的UP主动态规划入门课，通俗易懂：动态规划第一讲
动态规划第二讲的第一题
一位博主，总结的很不错：告别动态规划，DP连刷 40 道题，我总结出了这些套路！这应该是把动态规划讲的最后的文章了
动态规划第二讲第二题
二维dp问题：01背包问题

文章目录

dp引入：换钱（一维dp）
外卖小哥在一段时间内赚最多的钱（一维dp）
选出一组不相邻的数字且和最大（一维dp）
[总结] DP的解题经验
能不能凑出正整数s（二维dp）
01背包问题（二维dp）
dp有哪些类型

dp引入：换钱（一维dp）

原文链接：什么是动态规划？动态规划的意义是什么？)

【问题】你想把某宝里的666块换成现金，而且想换来的钱的总数最少，因为你的钱包快装不下了

【生活中的做法】从最大的面额开始换，以此可以获得数量最少的钞票，共10张。这种思想叫贪心，每经过一次，它会尽量让数值变得更小

$666 = 6 * 100 + 1 * 50 + 1 * 10 + 1 * 5 + 1 * 1$

【贪心的方法是对的吗？】如果钱的面额够科学，贪心就是对的。但是遇到这种情况：一个国家的钞票面额只有1、5、11。那我们这次用贪心来换15块

$15 = 1 * 11 + 4 * 1$ ，用贪心换得5张钞票
$15 = 3 * 5$ ，但最少的情况是这个，换得3张钞票

【贪心错在哪里？】鼠目寸光，只考虑了眼前的情况

【解决方案】我们用f(n)表示换n块所需的最小钞票的数量，那我们就有以下的情况

$f (1) = 1$ ：换1块钱，就只要一张1块
$f (4) = 4$ ：换4块钱，要4张1块
$f (5) = 1$ ：换5块钱，就只要1张5块
$f (10) = 2$ ：换10块钱，要2张5块
$f (11) = 1$ ：换11块钱，就只需要1张11块

理解的话，我们来换一下15块

$c o s t (15) = f (11) + f (4) = 1 + 4 = 5$ ：这种策略要5张
$c o s t (15) = f (5) + f (10) = f (5) + f (5) + f (5) = 3$ ：这种策略要3张
$c o s t (15) = f (1) + f (14) = 1 + 4 = 5$ ：这种策略只要5张

那我们要的就是3个中最小的情况，于是有公式：

f(n)=min{ f(n-1), f(n-5), f(n-11) } +1

有了这个公式怎么暴力求解呢？

int f_0(int n) { //用递归暴力求解int mincost = 65535;if (n==0) return 0;if (n>=1) mincost = min(mincost, f_0(n-1)+1);if (n>=5) mincost = min(mincost, f_0(n-5)+1);if (n>=11) mincost = min(mincost, f_0(n-11)+1);printf("f[n]=%d\n", n, mincost);return mincost;
}

此过程会生成一个递归树，由于最小面额为1，所以树的高度为n，则把树当成满二叉树来算结点总数 $2^n-1$ ，故此方法的时间复杂度为 $O(2^n)$

在这里插入图片描述

改良1：用数组保存之前的计算结果，避免重复计算，复杂度O(n)。这就是dp，暂时可以把dp理解成用数组记录历史记录的递归或递推

int min(int a, int b) {return a>b?b:a;
}
int f_1(int n) { int i, mincost, f[105];f[0]=0;for (i=1; i<=n; ++i) { //递推的方式：从下往上算mincost = 65535;if (i>=1) mincost = min(mincost, f[i-1]+1);if (i>=5) mincost = min(mincost, f[i-5]+1);if (i>=11) mincost = min(mincost, f[i-11]+1);f[i]=mincost;}return f[n];
}f[105]={0};		 //把每次计算的值保存下来
int f_2(int n) { //递归的方式：从上往下找需要算的内容int mincost = 65535;if (n==0) return 0;if (n>=1) mincost = min(mincost, f[n-1]==0 ? f_2(n-1)+1: f[n-1]+1 );//看f[n-1]之前有没有算过（有个装逼名字叫：记忆化搜索）if (n>=5) mincost = min(mincost, f[n-5]==0 ? f_2(n-5)+1: f[n-5]+1 );if (n>=11) mincost = min(mincost, f[n-11]==0 ? f_2(n-11)+1: f[n-11]+1 );f[n]=mincost;printf("f[%d]=%d\n", n, f[n]); //看到底计算了谁return mincost;
}

对比：暴力<动态规划<贪心（从效率和使用条件的角度）

【贪心】上面所提，贪心的问题在于鼠目寸光，但只要面额设置的足够科学，贪心是对的。这可以说明，使用贪心的条件是很苛刻严格的，要经过严格的数学证明，才能够确定根据局部最优所得的结果对不对。
【贪心vs动态规划】但对于动态规划。它在哪种面额下都是可以的，这可以说明，动态规划(dp)的条件相比于贪心是更不苛刻的，正是因为贪心更严格，所以贪心的效率更高
【动态规划vs暴力】从上面可以看到，动态规划没有重复计算、也减去了没有必要的计算内容。减去不必要的计算任务，我们叫剪枝。也就是说动态规划自带剪枝，这是动态规划优于暴力的地方。

看到这里，相信你对DP有初步的了解。如果对自己没有信心，不要立刻看DP的严格定义。继续看一些例子，加深对它的感性认识。直到你对它有所感悟的时候，而且感悟到达极点的时候，再去看别人的总结，会恍然大悟，瞬间打通所有。

外卖小哥在一段时间内赚最多的钱（一维dp）

链接：动态规划 (第1讲)

题目：外卖小哥想在11个小时内赚最多的钱

横条前的数字：第i个外卖单子，一共有8个单子
横条的长度：做该单需要花费的时间段
横条上的红色数字：完成该单的报酬

【思路】选与不选
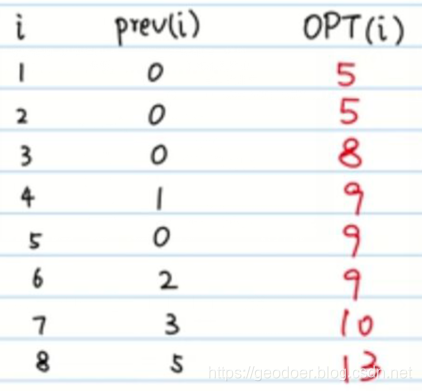
【抽象问题】OPT[i]：完成前i项单子，赚的最多的钱

OPT[1]：完成前1项单子，最多能赚5块（完成第一单）
OPT[2]：完成前2项单子，最多能赚5块（只做第一单）
OPT[3]：完成前3项单子，最多能赚8快（只做第三单）
OPT[4]：完成前4项单子，最多能赚8块（只做第三单）
OPT[8]：怎么算？

【OPT[8]】完成前8项单子赚的最多的钱，那就有两种可能：对于第8项单子，我是做，还是不做

做第8个单子：然后8-11的时间段就不能做别的了，所以只能做8之前的单子，这里记做pre[8]
不做第8个单子：那就是OPT[7]

然后在两种情况下找到最大值，即是OPT[8]，于是有以下公式：
在这里插入图片描述

【pre[]】pre数组怎么求呢？根据每个单子的结束时间来确定

【最终答案】
在这里插入图片描述

选出一组不相邻的数字且和最大（一维dp）

链接：动态规划第二讲第一题

题目：在一个数组arr中，找出一组不相邻的数字，使得最后的和最大
在这里插入图片描述

#include<stdio.h>
int max(int a, int b) {return a>b?a:b;
}int dp_1(int arr[], int n) { //非递归int opt[105];int i;//初态opt[0]=arr[0];opt[1]=max(arr[0], arr[1]);//通式（选、不选中的最大值）：opt[i] = max{ opt[i-1], arr[i]+opt[i-2] }for (i=2; i<n; ++i) {opt[i] = max( opt[i-1], arr[i]+opt[i-2] );printf("opt[%d]=%d\n", i, opt[i]);}return opt[n-1];
}int opt[105] = {0}; //保存记录
int dp_2(int arr[], int n) { //递归int i=n-1; //arr从0开始存储if (opt[i]!=0) return opt[i]; //计算过了if (i==0) {opt[i]=arr[0];return opt[i];} else if (i==1) {opt[i]=max(arr[0], arr[1]);return opt[i];} else {if (opt[i-1]==0) opt[i-1] = dp_2(arr, n-1);if (opt[i-2]==0) opt[i-2] = dp_2(arr, n-2);opt[i] = max( opt[i-1], arr[i]+opt[i-2] );printf("opt[%d]=%d\n", i, opt[i]);return opt[i];}
}int main() {int arr[105] = {1, 2, 4, 1, 7, 8, 3};printf("%d", dp_2(arr, 7) ); //前7个数字return 0;
}

[总结] DP的解题经验

原文链接：告别动态规划，DP连刷 40 道题，我总结出了这些套路！这应该是把动态规划讲的最后的文章了

【步骤一】确定数组

梳理问题的条件
确定数组维度：一般影响因子有几个，数组就有几个维度
准确定义数组的含义

【步骤二】找出数组元素之间的关系

从末态找
分析问题的过程

【步骤三】找出初始值，即出口（从初态找）

找初始值容易出错，有时候容易找的不完整，所以不能仅局限于在数组元素中下标>=0的程度，要多考虑几位

【注意】

下标问题：下标一般存1-n，0可以作为边界检查、也不容易搞乱

能不能凑出正整数s（二维dp）

链接：动态规划第二讲第二题

【题目】给定一个正整数s, 判断一个数组arr中，是否有一组数字加起来等于s
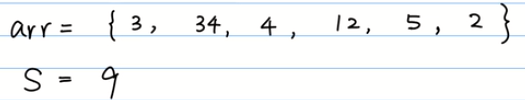
在这里插入图片描述

【第一步】确定数组

确定问题：①选数字；②数字和等于S；③问题：能不能选出这么一组数字
数组维数：影响因子是①数字之和、②单个数字 --> 二维dp
定义数组含义（即问题）：Subset[k][s]：从前k个元素中选一组数字，它们的和是s，subset[k][s]等于1表示能选出来

【第二步】确定元素间的关系
从后往前，当前数字是选还是不选，只要其中一个能凑出，就返回true
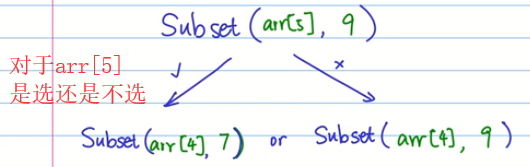
在这里插入图片描述
【第三步】找初始值，也就是出口

s==0：空集就好了，这时候返回true
k==0：只有0可以选了，如果这时候第0个数值刚好是s，则返回true，否则返回false

【代码】

#include<stdio.h>
#include<string.h>// 从arr[]中的前k个元素中，选择一组元素，它们的和刚好等于s，则返回1
int dp[105][105]; //数组
int dp_rec(int arr[], int k, int s) { //递归int val1, val2;if (dp[k][s]!=-1) return dp[k][s]; //有历史记录，直接返回// 递归出口if (s==0) dp[k][s]=0;else if (k==0) dp[k][s] = arr[0]==s;// 通式else if (arr[k]>s) //选了第k个就超出了s，那不选dp[k][s] = dp_rec(arr, k-1, s);	else {val1 = dp_rec(arr, k-1, s); //不选val2 = dp_rec(arr, k-1, s-arr[k]); //选第k个dp[k][s] =  val1 || val2;}printf("dp[%d][%d]=%d\n", k, s, dp[k][s]);return dp[k][s];
}int main() {int i,j;// 测试int n=6;int s=9;int arr[6] = {3, 34, 4, 12, 5, 2}; //0到n-1memset(dp, -1, sizeof(dp));printf("\n可以凑到吗？ %d\n", dp_rec(arr, n-1, s) );for (i=0; i<n; i++) {for (j=0; j<n; j++)printf("%d\t", dp[i][j]);printf("\n");}return 0;
}

01背包问题（二维dp）

视频链接：01背包问题
链接：01背包在线计算器

【题目】有n个物品及它们的重量和价格，问小偷的背包只能装下20kg，怎么装偷的最多？
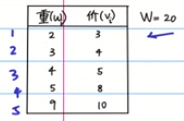
在这里插入图片描述
【步骤1】确定数组

确定问题：①选物品；②物品的总重量≤W；③问题：求物品的总价值最大
数组维数：影响因子是①物品的总重量、②单个物品的重量 --> 二维dp
定义数组含义（即问题）：B[k][w]：在前k个商品中选取一组商品，重量≤w，物品总价值最大为B[k][w]

【步骤2】找出数组元素的关系
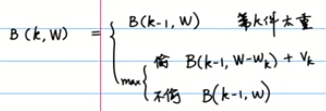
在这里插入图片描述

【步骤3】找初始值

B[0][0]->B[0][w]（第一行）都为0：没有物品时，最大价值为0
B[0][0]->B[k][0]（第一列）都为0：有物品，没有包来装，最大价值也是0

B(k,w)数组的值：
在这里插入图片描述
【代码】

#define N 5   //5个商品
#define W 20  //背包重量
int B[N+1][W] = {0};
int w[N+1] = {0, 2,3,4,5,9}; //从1-N开始记录
int v[N+1] = {0, 3,4,5,8,10}; //从1-N开始记录
void Knapsack(int B[N+1][], int w[], int v[]) {int i,j;int val1, val2;// 初始值（其实不用赋予初始值，B[][]数组定义时初始值即为0）for (j=0; j<=W; ++j) B[0][j]=0; //第一行for (i=0; i<=N; ++i) B[i][0]=0; //第一列// 递推for (i=1; i<=N; ++i) { //考虑前k个物品for (j=1; j<=W; ++j) { //背包的重量if ( w[i] > j ) { //第i件物品太重，背包已经装不下了B[i][j] = B[i-1][j]; //不考虑第i件} else {val1 = B[i-1][j];    //不选第i件val2 = B[i-1][j-w[i]]+v[i]; //选第i件B[i][j] = val1>val2 ? val1 : val2;}}}
}