本文主要是介绍15 ABC基于状态机的按键消抖原理与状态转移图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 基于状态机的按键消抖
1.1 什么是按键?
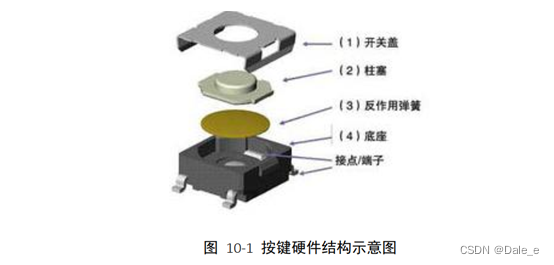

从按键结构图10-1可知,按键按下时,接点(端子)与导线接通,松开时,由于弹簧的反作用力,接点(端子)与导线断开。
从原理图10-2可知,按键按下时为低电平,未按下为高电平
1.2 为什么要消抖?
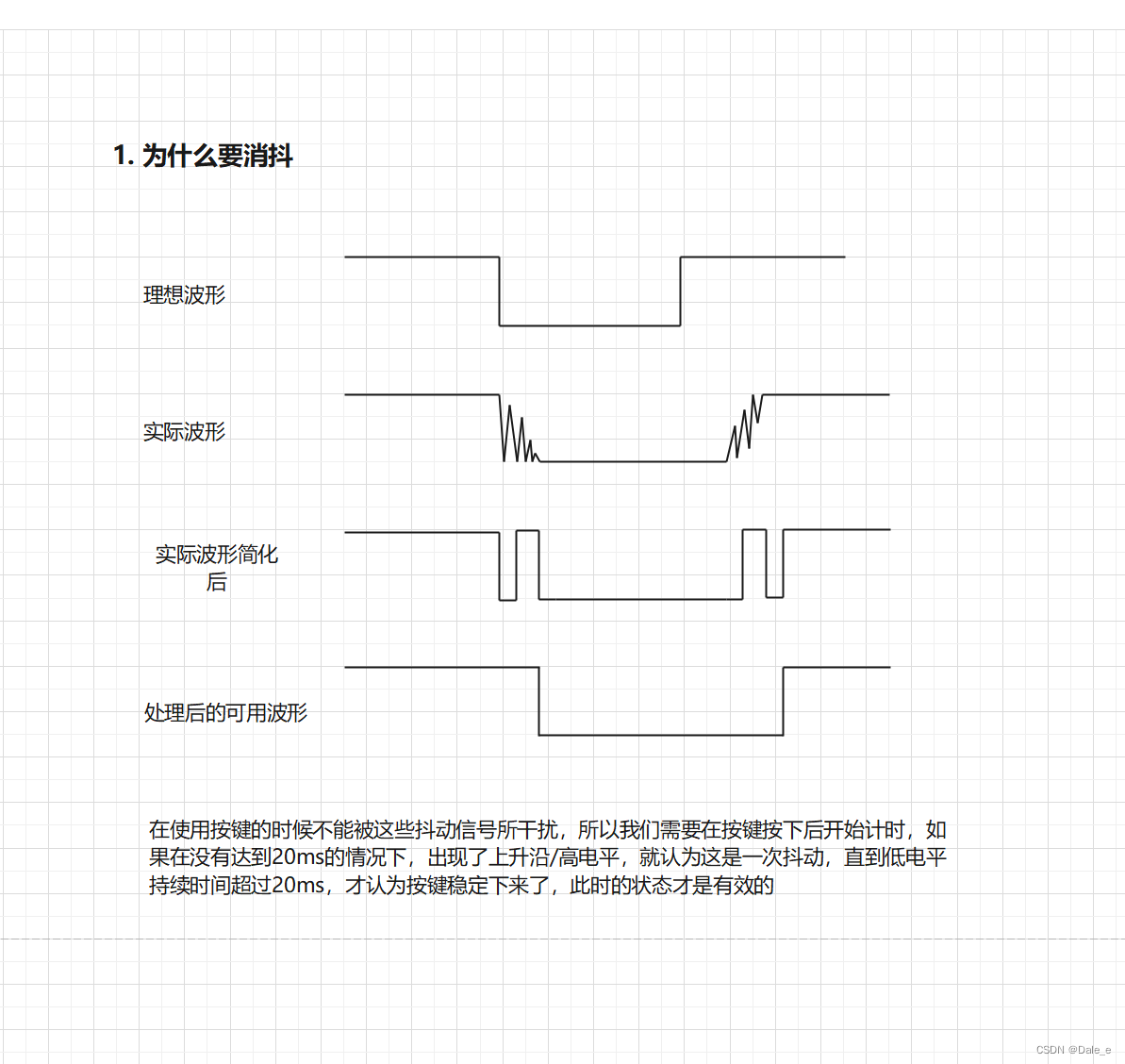
1.3 基于按键消抖的状态转移图

2. 写设计代码,仿真代码并仿真(未使用随机函数的测试)
1. 设计代码
module key_filter(clk,rstn,key,
// key_p_flag,
// key_r_flag,key_flag,key_state
);input clk;input rstn;input key;
// output reg key_p_flag;
// output reg key_r_flag;output reg key_flag;output reg key_state;//边沿检测reg [1:0] r_key;always@(posedge clk)r_key <= {r_key[0], key};
// reg [1:0] r_key;
// always@(posedge clk)begin
// r_key[0] <= key;
// r_key[1] <= r_key[0];
// endwire nedge_key;wire pedge_key;assign nedge_key = (r_key == 2'b10);assign pedge_key = (r_key == 2'b01);reg [1:0]state;reg [19:0] cnt;always@(posedge clk or negedge rstn)if(!rstn)beginstate <= 0;cnt <= 0;
// key_p_flag <= 0;
// key_r_flag <= 0;key_flag <= 0;key_state <= 1;endelsecase(state)0: begin
// key_r_flag <= 0;key_flag <= 0;if(nedge_key == 1) beginstate <= 1;endelsestate <= 0;end 1:beginif((pedge_key == 1) && (cnt < 1000000 - 1))beginstate <= 0;cnt <= 0;endelse if((pedge_key == 0) && (cnt >= 1000000 - 1))beginstate <= 2;
// key_p_flag <= 1'd1;key_flag <= 1'd1;key_state <= 0;cnt <= 0;endelsecnt <= cnt + 1'd1;end2:begin
// key_p_flag <= 0;key_flag <= 0;if(pedge_key == 1)state <= 3;elsestate <= 2;end3:beginif((nedge_key == 1) && (cnt < 1000000 - 1))beginstate <= 2;cnt <= 0;endelse if((nedge_key == 0) && (cnt >= 1000000 - 1))beginstate <= 0;
// key_r_flag <= 1;key_flag <= 1'd1;key_state <= 1;cnt <= 0;endelsecnt <= cnt + 1'd1;endendcaseendmodule
2. 仿真代码
`timescale 1ns / 1psmodule key_filter_tb();reg clk;reg rstn;reg key;
// wire key_p_flag;
// wire key_r_flag;wire key_flag;wire key_state;key_filter key_filter_inst(.clk(clk),.rstn(rstn),.key(key),
// .key_p_flag(key_p_flag),
// .key_r_flag(key_r_flag),.key_flag(key_flag),.key_state(key_state));initial clk = 1;always #10 clk = ~clk;initial beginrstn = 0;key = 1;#201;rstn = 1;#200;key = 1;#50000000;key = 0;#30000;key = 1;#30000;key = 0;#30000;key = 1;#30000;key = 0;#50000000;key = 1;#30000;key = 0;#30000;key = 1;#30000;key = 0;#30000;key = 1;#50000000;$stop;endendmodule
3. 仿真波形
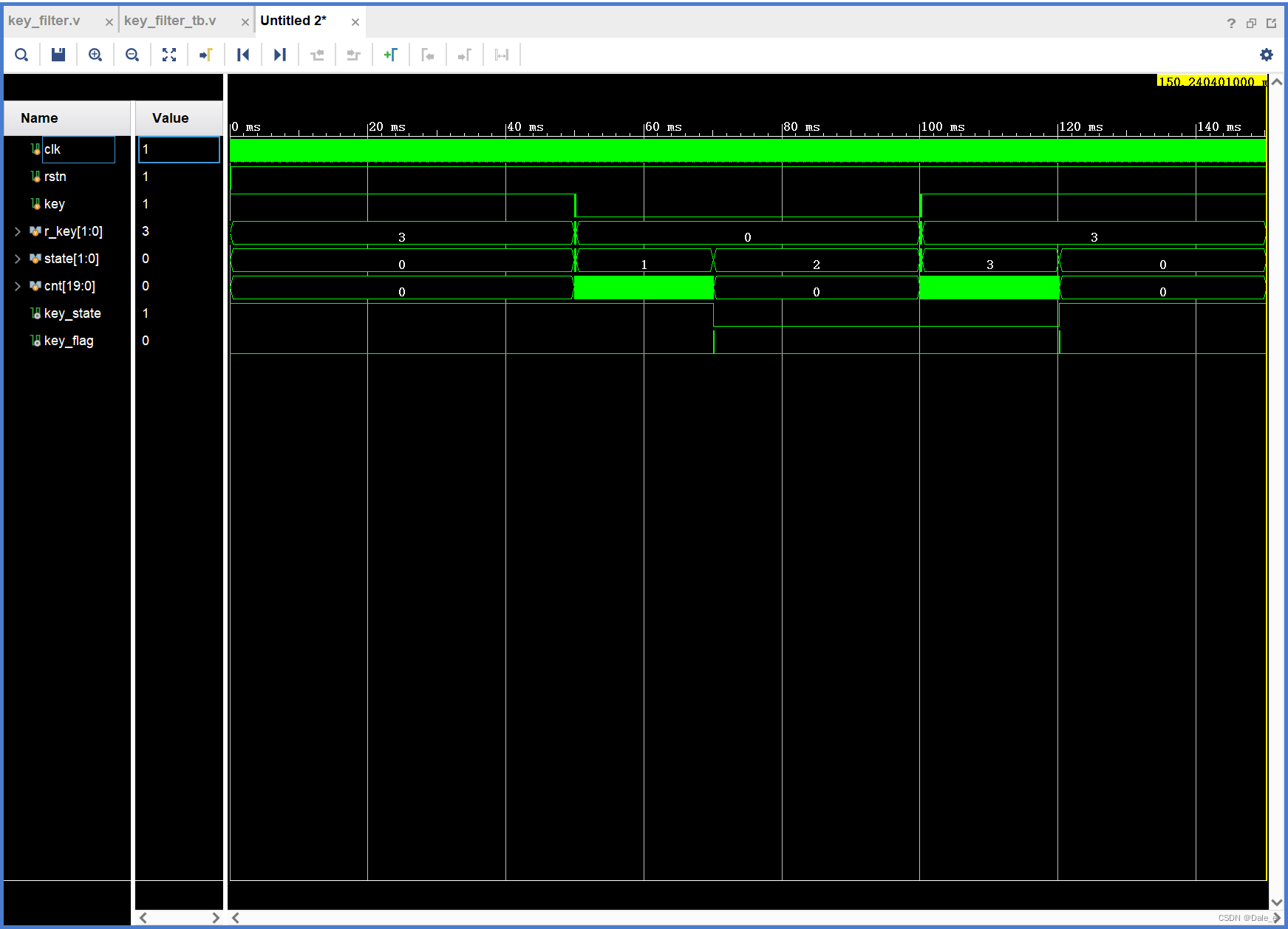
3. 基于verilog系统函数random的随机测试下的按键抖动(tb编写语法)
通过系统函数random产生一个随机的延迟值,来模拟真实情况下的延迟。


3.1 系统函数random的两个例子:
1. 产生一个[-(b+1): (b-1)]的随机数:$random% b;
2.产生一个[0: b-1]的随机数:{$random}% b;;
修改后的仿真代码:
`timescale 1ns / 1psmodule key_filter_tb();reg clk;reg rstn;reg key;
// wire key_p_flag;
// wire key_r_flag;wire key_flag;wire key_state;key_filter key_filter_inst(.clk(clk),.rstn(rstn),.key(key),
// .key_p_flag(key_p_flag),
// .key_r_flag(key_r_flag),.key_flag(key_flag),.key_state(key_state));initial clk = 1;always #10 clk = ~clk;reg [19:0] rand;initial beginrstn = 0;key = 1;#201;rstn = 1;#200;press_key(1);$stop;endtask press_key;input [2:0] seed;beginkey = 1;#20000000; repeat(5) beginrand = {$random(seed)} % 9999999; //产生0到9999999ns的延迟#rand key = ~key;endkey = 0;#40000000;repeat(5) beginrand = {$random(seed)} % 9999999; //产生0到9999999ns的延迟#rand key = ~key;endkey = 1;#40000000;endendtaskendmodule
4. 调试(产生多余38ns的原因)
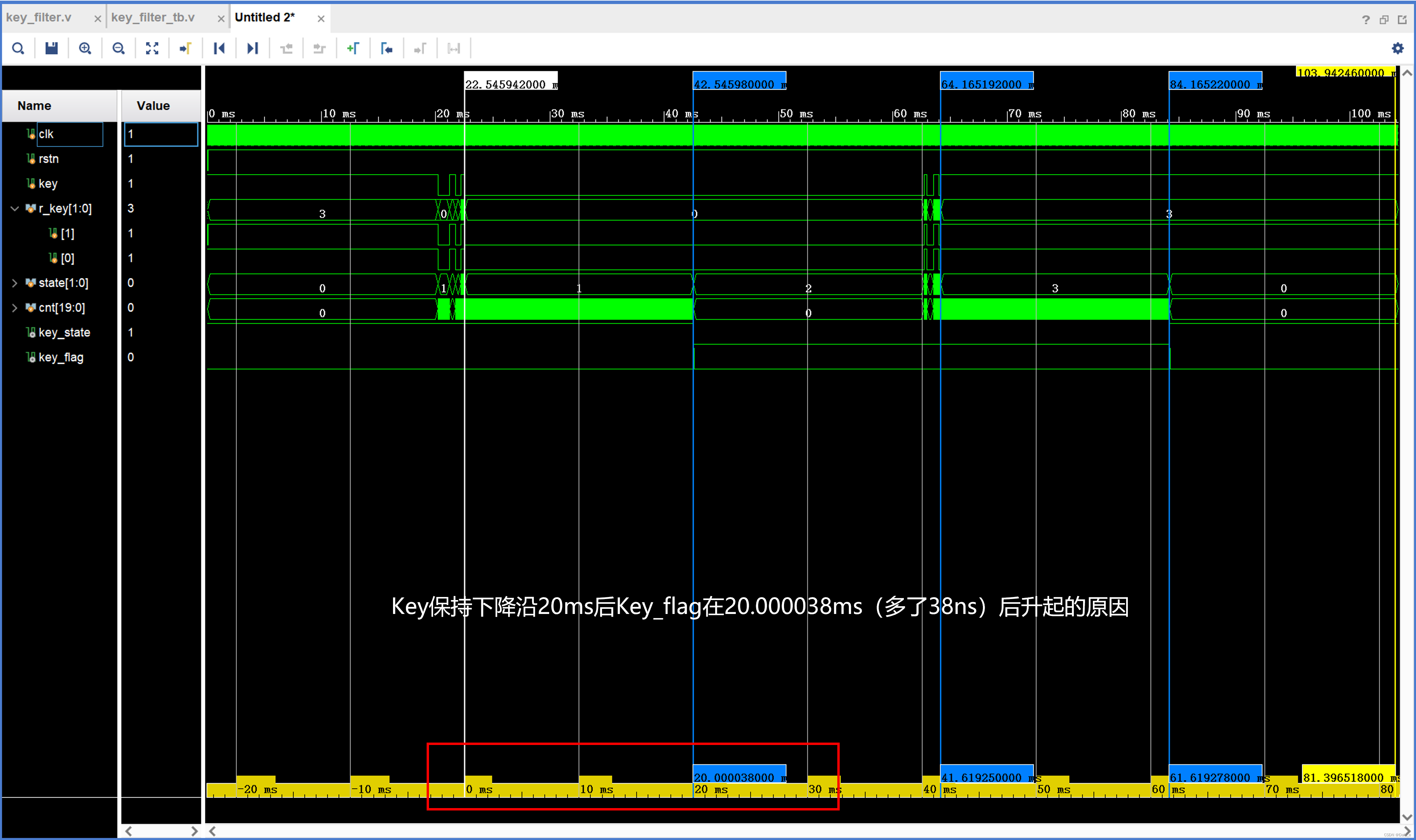
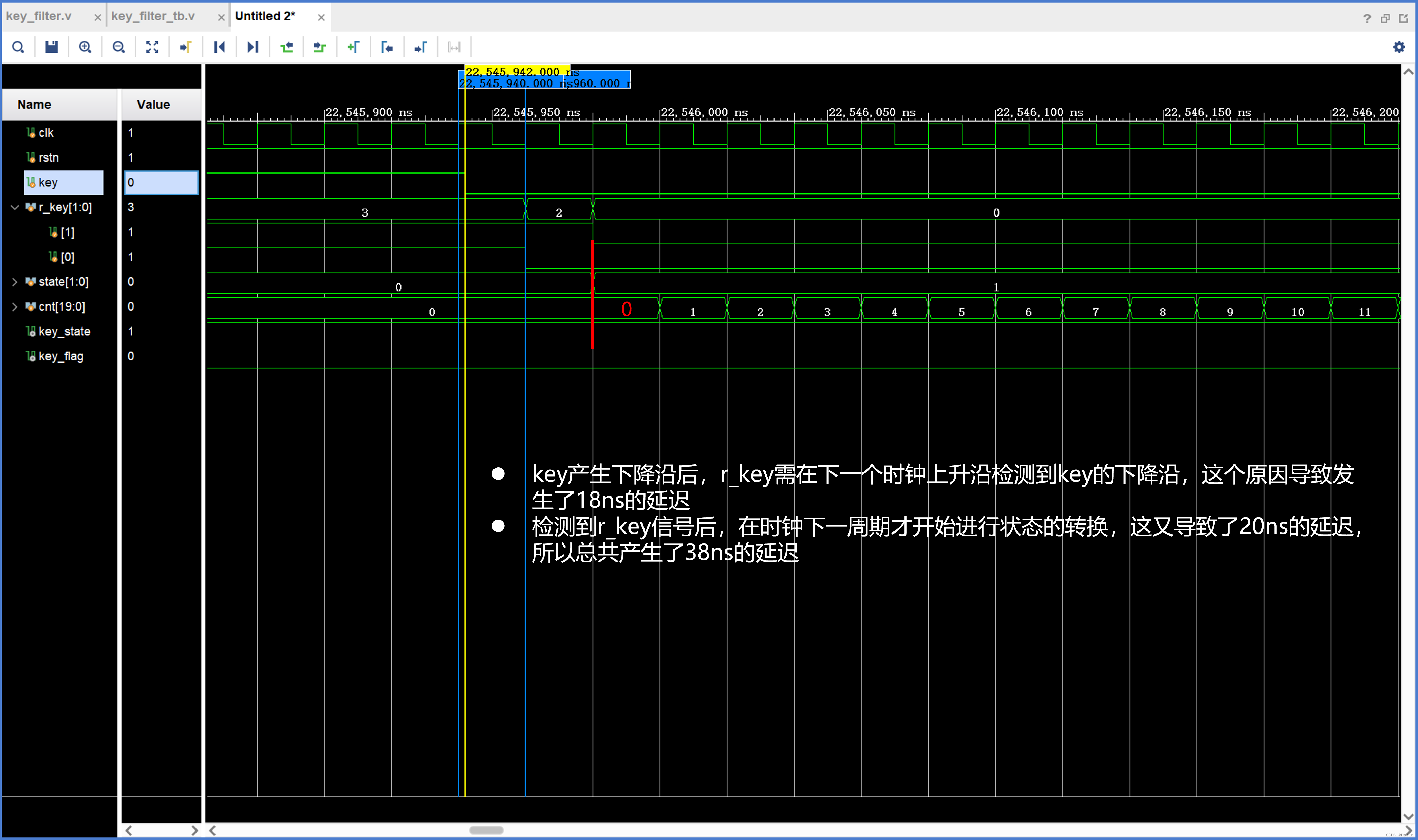
这篇关于15 ABC基于状态机的按键消抖原理与状态转移图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





