abc专题
js中怎样对“abc”进行MD5、sha256哈希计算?
在 JavaScript 中,可以使用 CryptoJS 库来进行 MD5 哈希计算。首先,你需要在 HTML 文件中导入 CryptoJS 库,例如: <script src="https://cdnjs.cloudflare.com/ajax/libs/crypto-js/3.1.9-1/crypto-js.min.js"></script> 然后,在 JavaScript 文件中,可
【ZOJ】3881 From the ABC conjecture【暴力容斥】
传送门:【ZOJ】3881 From the ABC conjecture 复杂度大概 O(N0.67) O(N^{0.67}),我也不会算www,首先转换一下(我们是根据积性函数打表找规律得到的,也可以推出来)使得: g(N)=∏pi ϵ N(pia+1) g(N)=\prod_{pi~\epsilon ~N} (pi^a+1) 暴力展开发现贡献为: h(N)=
题解AtCoder ABC 358 F Easiest Maze
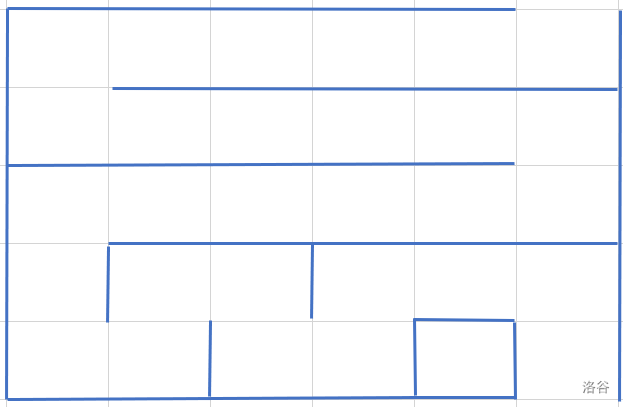
一道模拟题。 思路 最短的路线是直接竖着走下来,经过 n n n 个格子,所以 k k k 最小是 n n n。如果想要延长路线,可以采用九转大肠的形状,就像这样: 可以发现,每次向左走之后都必须走回来,所以每次新经过的格子数是偶数,得到 k − n k-n k−n 是偶数才有可行的方案。 首先,把整张图表的初始状态设为如下形式(即每个格点都是独立的): +++++S++o|o|o
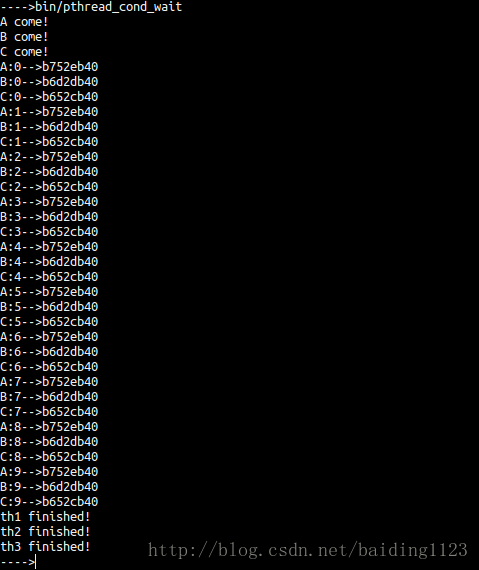
面试算法题:三线程循环打印ABC
面试遇到三线程循环打印ABC的题目,当时没写出来,然后经过查阅,进行整理了一下。 1、题目 有A、B、C 三个线程,A线程 输出“A”,B线程 输出“B”,C线程 输出“C”,要求同时启动3个线程,按照顺序输出“ABC”,循环10次,请使用代码实现。 2、问题分析 A、B、C 三个线程;这表示我们要使用多线程同步,有人说了这不废话吗。是的,笔者只是想说,多线程的实现,有几种方式,①继承Th
[Algorithm][综合训练][小葱的01串][小红的ABC][不相邻取数]详细讲解
目录 1.小葱的01串1.题目链接2.算法原理详解 && 代码实现 2.小红的ABC1.题目链接2.算法原理详解 && 代码实现 3.不相邻取数1.题目链接2.算法原理详解 && 代码实现 1.小葱的01串 1.题目链接 小葱的01串 2.算法原理详解 && 代码实现 解法:滑动窗口 --> ⻓度固定的滑动窗⼝,要想符合要求,必定是⼀半⼀半的 选择区域的时候,仅需
ABC 368 G - Add and Multiply Queries
原题链接:G - Add and Multiply Queries 题意:给出数组a和b,三种操作,第一种:以 1 i x 的形式给出。用x替换ai。第二种:以 2 i x 的形式给出。用x代替 bi 。第三种:以3 l r的形式给出,初始值为0,从l到r每个位置上可以选择加上a[i],或者乘上b[i],输出最大值。 思路:链表+set+树状数组+二分。题目中给出了答案的范围不会超过1e1
abc 366 E+F(曼哈顿距离 x y 两个坐标分别计算)(贪心+01背包)
E题: 题意:给定的 xi yi 。求有多少点 到给人 若干定点 的曼哈顿距离 和 小于等于D. 因为D 最大时 1e6,-1e6<=xi<=1e6。 所以 可能的 点 的 x 的范围是 [-2e6 2e6] 同理 y 的 范围 一样。 将 x y 分开讨论。 我们可以枚举 某个x 的 个数,找到合法的y 的个数。两者相乘。相乘之后的值累加起来。就是结果。 碰到绝对值,利用排序,来消除绝对值。
反编译二进制格式的方舟字节码abc文件
本文记录如何反编译hap包中的adc文件 ## 1.解压hap包获取adc文件 首先解压想反编译的hap包  解压
ABC 362 E - Count Arithmetic Subsequences
原题链接:E - Count Arithmetic Subsequences 题意:给出长度为n的数组,要求找出所有的等差数列,并且按照长度递增输出。 思路:dp,因为是要找出等差数列,并且这题的数据量极小,所以可以考虑设计dp数组,dp[i][j][k][v],i代表当前寻找的等差数列倒数第二项,j代表最后一项,k代表还需要寻找的长度,v代表当前判断的数,dp[i][j][k][v]代表以i
每日一题~abc 367 F+luogu p10102(随机算法)
随机化的思想: 充分条件的计算代价比较大,想找个计算代价小的必要条件,但必要条件可能会出错,然后通过一些手段(比如随机映射)把这个出错的概率降低。(参考园子) 添加链接描述 题意: 两个数组,元素均为 1~N. q 次查询,判断 a b 数组,这一区间内的元素是否相同。(排列的顺序不重要,主要是元素的种类个数相同) n,q 均在2e5 内。 如果暴力,对每次查询,我们只能将这个区间内的所有数扫一
atcoder ABC 359-B题详解
atcoder ABC 359-B题详解 Problem Statement There are 2N people standing in a row, and the person at the i-th position from the left is wearing clothes of color Ai. Here, the clothes have N colors from 1
atcoder ABC 359-A题详解
atcoder ABC 359-A题详解 Problem Statement You are given N strings. The i-th string Si(1≤i≤N) is either Takahashi or Aoki. How many i are there such that Si is equal to Takahashi? Constraints 1≤N≤10
【Python】抽象基类——class BaseTrainer(abc.ABC)
在代码中看到class BaseTrainer(abc.ABC)这样的写法, 遂查了一下, 抽象基类(Abstract Base Class,ABC)。这里的abc是Python标准库中的abc模块,它提供了定义抽象基类的能力。通过继承自abc.ABC,BaseTrainer类可以包含抽象方法,强制要求任何继承它的子类必须实现这些抽象方法。这样的设计通常用于规定接口或者模板方法,增加代码的可扩
AtCoder ABC 365G 凸包 + 二分
题意 AtCoder ABC 365G Freestyle 题解 考虑任两种操作 ( A i , B i ) (A_{i},B_{i}) (Ai,Bi)和 ( A j , B j ) (A_{j},B_{j}) (Aj,Bj),则他们的任意组合可以表示为 ( t A i + ( 1 − t ) A j , t B i + ( 1 − t ) B j ) \big(tA_{i}+(1-
EIQ-ABC 分析法在配送中心储位分配中的应用
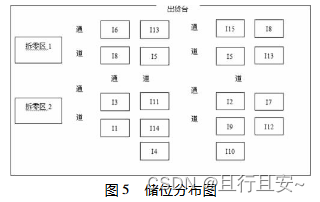
配送中心运作效率的高低主要取决于仓储业务流程的作业效率,在配送作业流程中,储位分配的是否合理性成为影响配送运作效率的重要因素。为实现储位的合理分配,提出通过对订单信息的分析,并应用 EIQ-ABC 分析法,以此实现缩短货物的搬运距离,降低搬运时间的目标,并通过案例对其进行分析。 ABC 分类法及 EIQ 分析法 1.1 ABC 分类法 ABC 分 类 法 其
atcoder ABC 358-B题详解
atcoder ABC 358-B题详解 Problem Statement At the entrance of AtCoder Land, there is a single ticket booth where visitors line up to purchase tickets one by one. The purchasing process takes A seconds p
atcoder ABC 357-C题详解
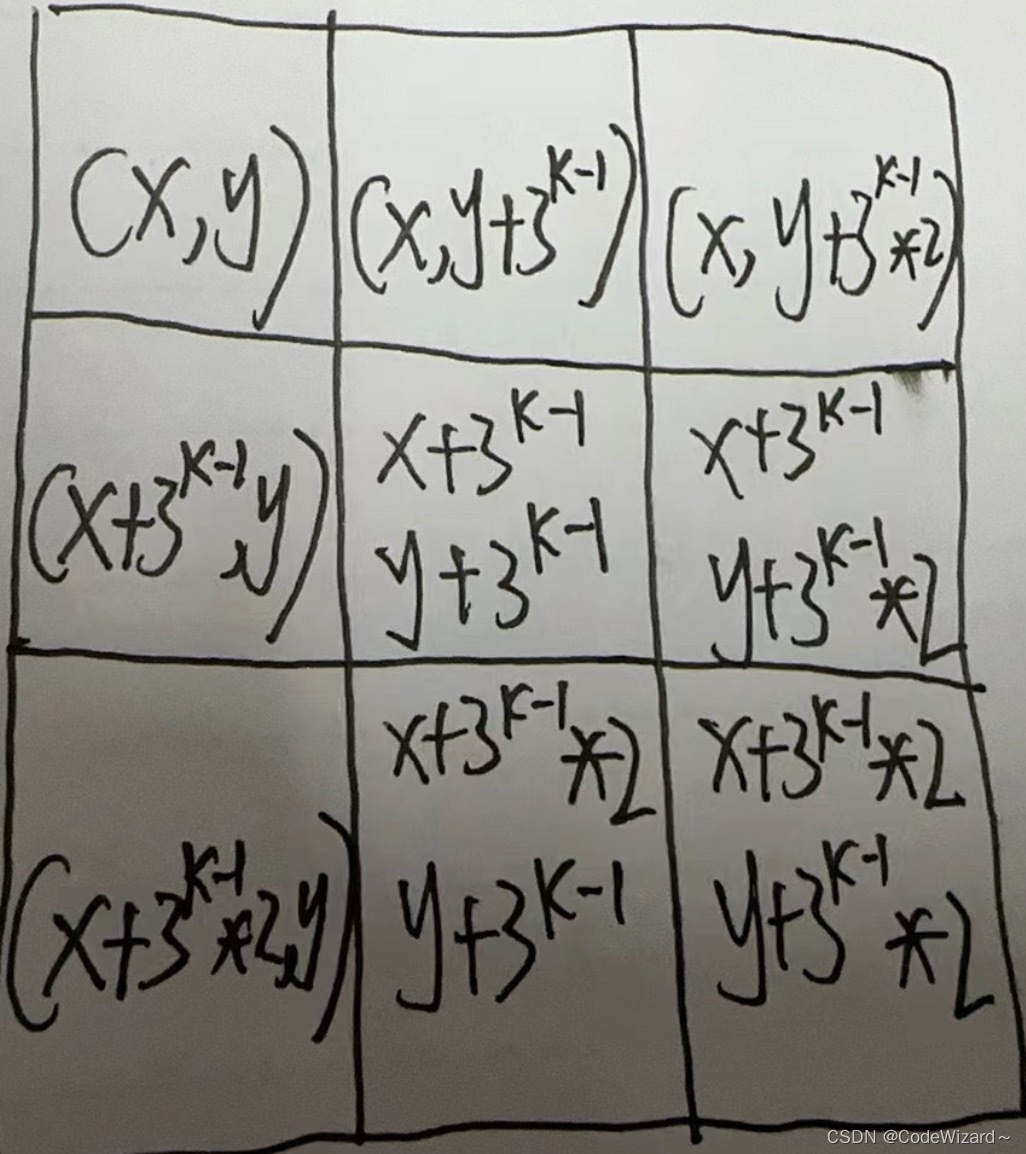
atcoder ABC 357-C题详解 Problem Statement For a non-negative integer K, we define a level-Kcarpet as follows: A level-0 carpet is a 1×1 grid consisting of a single black cell. For K>0, a level-K carp
ABC 357 G Stair-like Grid
link 其实是我之前写的一篇博客的推广 大意: 一个阶梯型,第 i i i行有 ⌈ i / 2 ⌉ ∗ 2 \left \lceil i/2 \right \rceil*2 ⌈i/2⌉∗2个方块,总共有n行。在其中给定 m m m个点无法经过,求从左上角到右下角的方案数。其中每次移动只能向右或向下 N ≤ 2.5 e 5 , M ≤ 50 N\leq 2.5e5,M\leq 50 N≤2.5
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
class Solution { private: string temp; private: vector<string> result; public: vector<string> Permutation(string str) { vector<string> result; //创建字符串数组 int len = str.length(); //求出字符串
Mac下删除系统自带输入法ABC,正解!
一、背景说明 MacOS 在 14.2 以下的系统存在中文输入法 BUG,会造成系统卡顿,出现彩虹圆圈。如果为了解决这个问题,有两种方法: 升级到最新的 14.5 系统使用第三方输入法 在使用第三方输入法的时候,会发现系统自带的 ABC 输入法无法删除,在网上看过部分教程但是最后都不好用,主要是忽略了一点。 关键点在于在 com. apple. HIToolbox. Plist 删除 Ite
AtCoder Regular Contest 179 (ABC题)视频讲解
A - Partition Problem Statement You are given integers N N N and K K K. The cumulative sums of an integer sequence X = ( X 1 , X 2 , … , X N ) X=(X_1,X_2,\dots ,X_N) X=(X1,X2,…,XN) of length
线程池实现循环打印abc
思路:往线程池里面不断的扔任务,每个线程获取到锁后,判断能不能打印,能则打印后释放锁,不能则直接释放锁,直到打印出100个abc后关闭线程池。 package com.example.demo.multithread;import java.util.concurrent.CountDownLatch;import java.util.concurrent.ExecutorService;
编写一个程序,开启3个线程,这3个线程的ID分别为A、B、C,每个线程将自己的ID在屏幕上打印10遍,要求输出结果必须按ABC的顺序显示;如:ABCABC….依次递推
编写一个程序,开启3个线程,这3个线程的ID分别为A、B、C,每个线程将自己的ID在屏幕上打印10遍,要求输出结果必须按ABC的顺序显示;如:ABCABC….依次递推。 好长时间没有再想写代码了,虽然自己还没有毕业,处于学习的阶段,但是很少是主动的写过多少,代码量太少是一大障碍。在不久就面临毕业找工作,刚才看了许久的各大公司的笔试题,看懂的没有几道,会的更
2022全国大学生数学建模竞赛ABC题(论文+代码)
文章目录 (1)2022A波浪能最大输出功率(2)2022B无人机定位(3)2022C古代玻璃制品成分分析(4)论文和代码链接 (1)2022A波浪能最大输出功率 (2)2022B无人机定位 (3)2022C古代玻璃制品成分分析 (4)论文和代码链接 祝大家成功 有需要的请:见下图
优化算法——人工蜂群算法(ABC)
一、人工蜂群算法的介绍 人工蜂群算法(Artificial Bee Colony, ABC)是由Karaboga于2005年提出的一种新颖的基于群智能的全局优化算法,其直观背景来源于蜂群的采蜜行为,蜜蜂根据各自的分工进行不同的活动,并实现蜂群信息的共享和交流,从而找到问题的最优解。人工蜂群算法属于群智能算法的一种。 二、人工蜂群算法的原理 1、原理 标准的ABC算法通过模拟实际蜜