本文主要是介绍代码随想录算法训练营第二十九天 |491.递增子序列,46.全排列,47.全排列II(待补充),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
491.递增子序列
1、题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2、文章讲解:代码随想录
3、题目:
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
4、视频链接:
回溯算法精讲,树层去重与树枝去重 | LeetCode:491.递增子序列_哔哩哔哩_bilibili
5、思路:
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的90.子集II(opens new window)。
就是因为太像了,更要注意差别所在,要不就掉坑里了!
在90.子集II(opens new window)中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
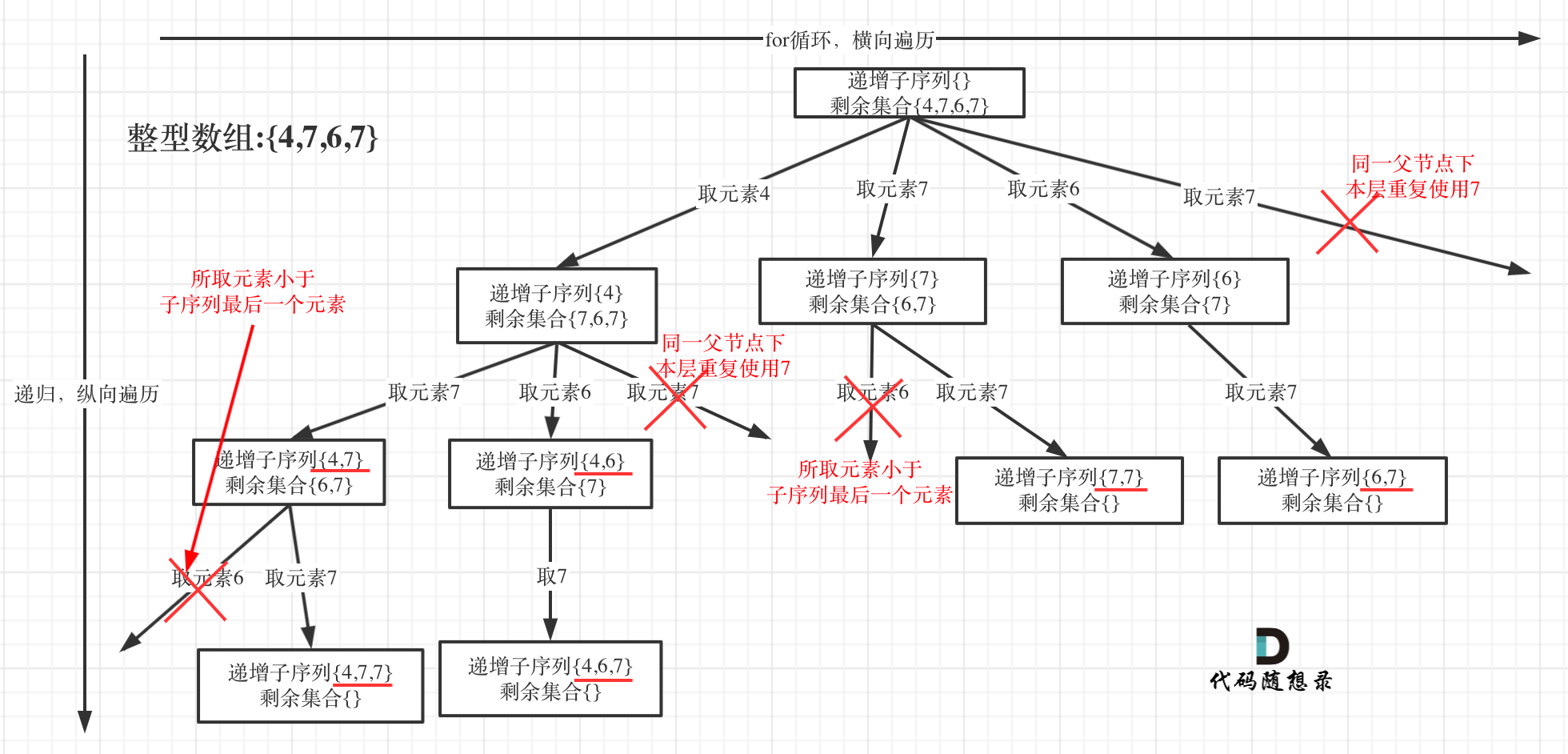
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}private void backTracking(int[] nums, int startIndex) {// 递增子序列的长度至少是2if (path.size() >= 2) {result.add(new ArrayList<>(path));// 注意这里不要加return,因为要取树上的所有节点}// 定义一个hashset来剪枝HashSet<Integer> hs = new HashSet<>();for (int i = startIndex; i < nums.length; i++) {// 剪枝// 1. path里已经包含的元素// 2. 当前元素比path里最后一个元素还小// 3. 当前元素已经在hs里了if (!path.isEmpty() && path.get(path.size() - 1) > nums[i] || hs.contains(nums[i])) {continue;}hs.add(nums[i]);path.add(nums[i]);backTracking(nums, i + 1);path.removeLast();}}
}46.全排列
1、题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2、文章讲解:代码随想录
3、题目:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
- 输入: [1,2,3]
- 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
4、视频链接:
回溯算法解决子集问题,树上节点都是目标集和! | LeetCode:78.子集_哔哩哔哩_bilibili
5、首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
class Solution {List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果public List<List<Integer>> subsets(int[] nums) {subsetsHelper(nums, 0);return result;}private void subsetsHelper(int[] nums, int startIndex) {result.add(new ArrayList<>(path));//「遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合」。if (startIndex >= nums.length) { // 终止条件可不加return;}for (int i = startIndex; i < nums.length; i++) {path.add(nums[i]);subsetsHelper(nums, i + 1);path.removeLast();}}
}47.全排列II
1、题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
2、文章讲解:代码随想录
3、题目:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
- 输入:nums = [1,1,2]
- 输出: [[1,1,2], [1,2,1], [2,1,1]]
示例 2:
- 输入:nums = [1,2,3]
- 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
4、视频链接:
回溯算法求解全排列,如何去重?| LeetCode:47.全排列 II_哔哩哔哩_bilibili
class Solution {// 存放结果List<List<Integer>> result = new ArrayList<>();// 暂存结果List<Integer> path = new ArrayList<>();public List<List<Integer>> permuteUnique(int[] nums) {boolean[] used = new boolean[nums.length];Arrays.fill(used, false);Arrays.sort(nums);backTrack(nums, used);return result;}private void backTrack(int[] nums, boolean[] used) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {// used[i - 1] == true,说明同⼀树⽀nums[i - 1]使⽤过// used[i - 1] == false,说明同⼀树层nums[i - 1]使⽤过// 如果同⼀树层nums[i - 1]使⽤过则直接跳过if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}// 如果同⼀树⽀nums[i]没使⽤过开始处理if (used[i] == false) {used[i] = true;// 标记同⼀树⽀nums[i]使⽤过,防止同一树枝重复使用path.add(nums[i]);backTrack(nums, used);path.remove(path.size() - 1);// 回溯,说明同⼀树层nums[i]使⽤过,防止下一树层重复used[i] = false;// 回溯}}}
}这篇关于代码随想录算法训练营第二十九天 |491.递增子序列,46.全排列,47.全排列II(待补充)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






