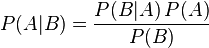机器学习经典算法详解及Python实现---朴素贝叶斯分类及其在文本分类、垃圾邮件检测中的应用

本文主要是介绍机器学习经典算法详解及Python实现---朴素贝叶斯分类及其在文本分类、垃圾邮件检测中的应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

摘要：

朴素贝叶斯分类是贝叶斯分类器的一种，贝叶斯分类算法是统计学的一种分类方法，利用概率统计知识进行分类，其分类原理就是利用贝叶斯公式根据某对象的先验概率计算出其后验概率（即该对象属于某一类的概率），然后选择具有最大后验概率的类作为该对象所属的类。总的来说：当样本特征个数较多或者特征之间相关性较大时，朴素贝叶斯分类效率比不上决策树模型；当各特征相关性较小时，朴素贝叶斯分类性能最为良好。另外朴素贝叶斯的计算过程类条件概率等计算彼此是独立的，因此特别适于分布式计算。本文详述了朴素贝叶斯分类的统计学原理，并在文本分类中实现了该算法。朴素贝叶斯分类器用于文本分类时有多项式模型和贝努利模型两种，本算法实现了这两种模型并分别用于垃圾邮件检测，性能显著。

Note：个人认为，《机器学习实战》朴素贝叶斯这一章关于文本分类的算法是错误的，无论是其贝努利模型（书中称“词集”）还是多项式模型（书中称“词袋”），因为其计算公式不符合多项式和贝努利模型。详见本文“文本分类的两种模型”。

（一）认识朴素贝叶斯分类

决策树算法中提到朴素贝叶斯分类模型是应用最为广泛的分类模型之一，朴素贝叶斯分类是贝叶斯分类器的一种，贝叶斯分类算法是统计学的一种分类方法，利用概率统计知识进行分类，其分类原理就是利用贝叶斯公式根据某对象的先验概率计算出其后验概率（即该对象属于某一类的概率），然后选择具有最大后验概率的类作为该对象所属的类。目前研究较多的贝叶斯分类器主要有四种分别是：朴素贝叶斯分类、TAN(tree augmented Bayes network)算法、BAN(BN Augmented Naive Bayes）分类和GBN（General Bayesian Network）。本文重点详细阐述朴素贝叶斯分类的原理，通过Python实现了该算法，并介绍了朴素贝叶斯分类的一个应用--垃圾邮件检测。

朴素贝叶斯的思想基础是这样的：根据贝叶斯公式，计算待分类项x出现的条件下各个类别（预先已知的几个类别）出现的概率P(y_i|x)，最后哪个概率值最大，就判定该待分类项属于哪个类别。训练数据的目的就在于获取样本各个特征在各个分类下的先验概率。之所以称之为“朴素”，是因为贝叶斯分类只做最原始、最简单的假设--1,所有的特征之间是统计独立的;2,所有的特征地位相同。那么假设某样本x有a₁,...,a_M个属性，那么有：

P(x)=P(a₁,...,a_M) = P(a₁)*...*P(a_M)

朴素贝叶斯分类发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率，其优点是算法简单、所需估计参数很少、对缺失数据不太敏感。理论上，朴素贝叶斯分类与其他分类方法相比具有最小的误差率，但实际上并非总是如此，因为朴素贝叶斯分类假设样本各个特征之间相互独立，这个假设在实际应用中往往是不成立的，从而影响分类正确性。因此，当样本特征个数较多或者特征之间相关性较大时，朴素贝叶斯分类效率比不上决策树模型；当各特征相关性较小时，朴素贝叶斯分类性能最为良好。总的来说，朴素贝叶斯分类算法简单有效，对两类、多类问题都适用。另外朴素贝叶斯的计算过程类条件概率等计算彼此是独立的，因此特别适于分布式计算。

（二）朴素贝叶斯分类数学原理

1，贝叶斯定理

贝叶斯定理是关于随机事件A和B的条件概率（或边缘概率）的一则定理。

其中P(A|B)是在B发生的情况下A发生的可能性。

在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。

P(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。

P(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。

P(B)是B的先验概率或边缘概率，也作

这篇关于机器学习经典算法详解及Python实现---朴素贝叶斯分类及其在文本分类、垃圾邮件检测中的应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---