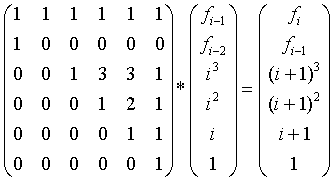2018年湘潭大学程序设计竞赛 - G - 又见斐波那契（矩阵快速幂）

本文主要是介绍2018年湘潭大学程序设计竞赛 - G - 又见斐波那契（矩阵快速幂），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：https://ac.nowcoder.com/acm/contest/105/G

思路：我们把上面式子的  加1变成：，还有就是然后我们构造矩阵：

总结一下就是把所给的公式在右边列出，原本公式左边列出，再求矩阵即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 6;
const int MOD = 1000000007;
ll n, k;
struct Matrix
{ll m[MAXN][MAXN];void init(int x){memset(m, 0, sizeof(m));for(int i = 0; i < MAXN; i++){m[i][i] = x;}}Matrix operator * (const Matrix &a) const{Matrix res;res.init(0);for(int i = 0; i < MAXN; i++)for(int j = 0; j < MAXN; j++)for(int k = 0; k < MAXN; k++)res.m[i][j] = (res.m[i][j] + (m[i][k] * a.m[k][j]) % MOD) % MOD;return res;}
};Matrix quickPow(Matrix x, ll p)
{Matrix res;res.init(1);x = x * res;while(p){if(p & 1) res = res * x;p >>= 1;x = x * x;}return res;
}Matrix a, x;void init()
{a = {1,1,1,1,1,1,1,0,0,0,0,0,0,0,1,3,3,1,0,0,0,1,2,1,0,0,0,0,1,1,0,0,0,0,0,1};x.m[0][0] = 1;x.m[1][0] = 0;x.m[2][0] = 8;x.m[3][0] = 4;x.m[4][0] = 2;x.m[5][0] = 1;
}int main()
{int T; scanf("%d",&T);while(T--){scanf("%lld",&k);init();a = quickPow(a, k - 1) * x;printf("%lld\n",a.m[0][0]);}return 0;
}

 

这篇关于2018年湘潭大学程序设计竞赛 - G - 又见斐波那契（矩阵快速幂）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---