CasMVSNet 论文学习：Cascade Cost Volume for High-Resolution Multi-View Stereo and Stereo Matching

论文解决的问题

本文提出了一种级联的思想，用来解决MVSNet和stereo matching中提出的3D代价体消耗过大的问题。构建三维代价体的目的是用来正则化并回归深度，并且可以适应任意数量的输入。但是随着代价体size增加，时间空间消耗是立方级增长的。因此提出了级联代价提的方法来进行corse-fine的调整。该方法在DTU准确度提升了35%，GPU和运行时间降了50%。主要的方法是：

• 使用FPN提取三个不同维度的特征图
• 每个特征图算作一个级联，动态降低深度假设范围和深度假设间隔，减小代价体大小
• 最终fuse构成更精细的深度图。

相关研究

在双目匹配和MVSNet算法中出现了3D代价体的概念，在训练空间时间消耗都很大。基于3D代价体的方法受限于下采样cost volume和最后通过插值生成高分辨率视差。

在MVS方法中主要有三类：volumetric方法，估计每个体素和表面之间的联系；点云方法，迭代处理点云来逐渐稠密结果，深度图预测，预测ref的深度图来合成。

实验方法

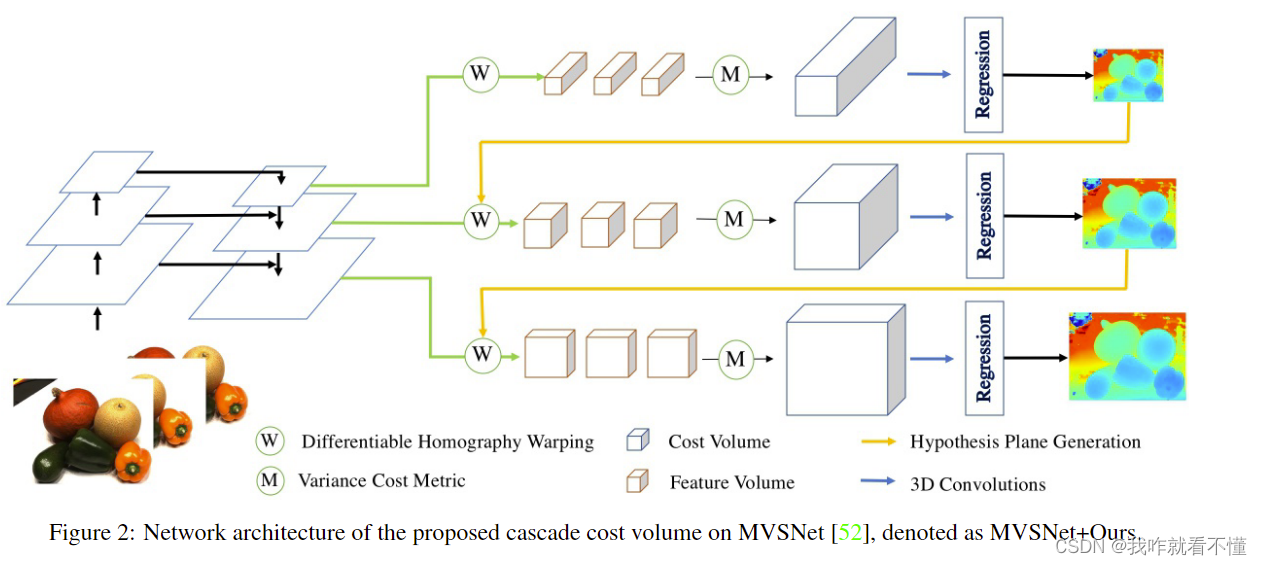
网络结构大概如图。围绕MVSNet进行改进。网络大致还是这几阶段，特征提取、代价体构建(深度范围假设)、代价体聚合、3D正则化、深度图生成。

特征提取

特征提取阶段不采用以往的仅类似编码器的特征提取网络，之前方法是首先通过MVSNet生成低分辨率的深度图，构建低分辨率的代价体，然后迭代优. 这样的构建方法只是用最终的特征图构建代价体.

这里采用不同分辨率的特征图构建代价体，实验中通过原输入图像尺寸大小的1/16, 1/4, 1的特征图构建三个代价体。

Homowarping/级联代价体聚合(关键)

这里是本文的关键.深度假设是代价体构建的重要步骤,以往的代价体构建都是使用固定的深度假设范围,如MVSNet中使用192,且深度的间距为定值.级联代价体通过上一次深度图预测的情况缩小本次深度假设范围.

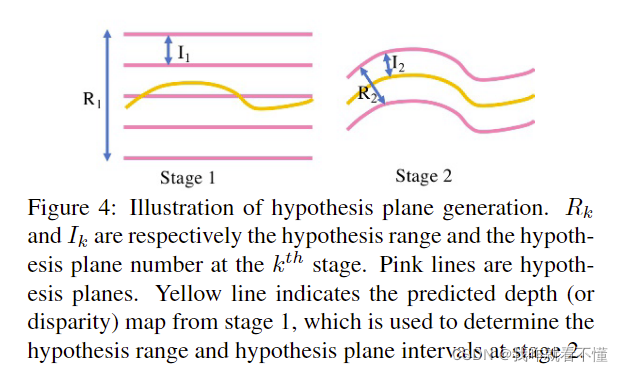
如图是示意图.在cascade第一阶段,没有上一阶段的深度假设,在本文中使用相对大的深度假设间隔,就是$I_1$,来生成粒度更大的深度假设图.粉色的线是假设深度,R1是深度估计范围.黄线是深度预测值.有了这个值进入下一阶段,就可以降低深度间隔和假设范围了.第二张图所示,R2是第二次的深度假设范围,I2是间隔,易知深度假设范围越小,相同resolution的代价体内存消耗越少.

文中也给了公式:

• 深度假设范围:$R_{k+1}=R_k\times w_k$
• 深度假设间隔 $I_{k+1}=I_k\times p_k$
• 假设平面个数 $D_k=\frac{R_k}{I_k}$

同时,在warping过程也与之前方法有不同

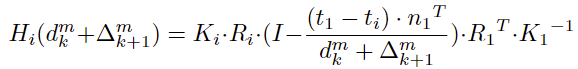
不同点在于该方法大的意思是在后面深度图估计时不学习整张深度图了,而是学习上一张深度图没有学习到深度的点(此公式还需学习理解)

级联网络,每一次级联输入的图像尺寸都在缩小,分别是1/16, 1/4, 1倍原图像.

Loss

和原来一样L1,只是在不同的stage计算的loss给上不同的参数加权起来.

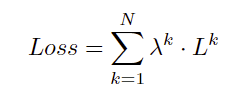
实验

三阶段级联是试出来的.3阶段之后效果趋于平稳,所以选择3级联.深度间隔分别设为4,2,1.

这个模块可以用在很多网络上.深度预测精度提升,GPU消耗降低.

消融:级联代价体3D卷积不共享参数效果更好,空间分辨率越高效果越好