本文主要是介绍Peter算法小课堂—枚举优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
哈哈哈,新年快乐!这一次Peter将要给大家讲一讲轻松、摆烂的算法—枚举!咋就是说呀,枚举这个玩意我语法就会了。但大家想想,咱们CSP考试时(除了没过初赛的)只给1秒,大家想想,这出题老师得有多抠啊。大伙们信不信,就这种easy的题,都配出进普及组,不管大家信不信,例题给我搬上来

[NOIP2016 普及组] 回文日期
题目描述
在日常生活中,通过年、月、日这三个要素可以表示出一个唯一确定的日期。
牛牛习惯用 8 位数字表示一个日期,其中,前 4 位代表年份,接下来 2 位代表月份,最后 2 位代表日期。显然:一个日期只有一种表示方法,而两个不同的日期的表 示方法不会相同。
牛牛认为,一个日期是回文的,当且仅当表示这个日期的 8 位数字是回文的。现在,牛牛想知道:在他指定的两个日期之间包含这两个日期本身),有多少个真实存在的日期是回文的。
一个 8 位数字是回文的,当且仅当对于所有的 i(1≤i≤8)从左向右数的第 i 个数字和第 9−i 个数字(即从右向左数的第 i 个数字)是相同的。
例如:
- 对于 2016 年 11 月 19 日,用 88 位数字 20161119 表示,它不是回文的。
- 对于 2010 年 1 月 2 日,用 88 位数字 20100102 表示,它是回文的。
- 对于 2010 年 10 月 2 日,用 88 位数字 20101002 表示,它不是回文的。
每一年中都有 12 个月份:
其中,1,3,5,7,8,10,12 月每个月有 31 天;4,6,9,11 月每个月有 30 天;而对于 2 月,闰年时有 29 天,平年时有 28 天。
一个年份是闰年当且仅当它满足下列两种情况其中的一种:
- 这个年份是 4 的整数倍,但不是 100 的整数倍;
- 这个年份是 400 的整数倍。
例如:
- 以下几个年份都是闰年:2000,2012,2016。
- 以下几个年份是平年:1900,2011,2014。
大家看道题给大家做个不用脑子的选择吧

当然,选B的人一定有那么一点点的**。这个选择题应该选 B D。
啊这,请大家 写一写代码 注意:看到这题千万别崩溃
先学两个语法吧,啥?语法?我学过了啊?
语法1
#include <bits/stdc++.h>
using namespace std;
int main(){string year="2019";reverse(year.begin(),year.end());cout<<year<<endl;int x[3]={7,8,9};reverse(x,x+3);cout<<x[0]<<x[1]<<x[2]<<endl;return 0;
}仔细观察此代码,有什么难以理解的地方。这叫“序列反转”。大家自己玩玩试试。当然,CSP时尽量多使用一些系统封装好的的函数,以免这个傻了吧唧调试几次没成功的,WA满天飞。
语法2
#include <bits/stdc++.h>
using namespace std;
void I2S(int x,string&str){stringstream ss;if(x<=9) ss<<0;ss<<x;ss>>str;
}
int main(){string s;I2S(1,s);cout<<s<<endl;I2S(12,s);cout<<s<<endl;return 0;
}这个属于int转string。来,看看&是什么,是引用传递!传递什么,传递地址啊,这可以让这个庞大的字符串变成轻量级的地址。
开始写代码八!
过亿会儿公布答案。
噔噔噔噔,公布答案啦
#include <bits/stdc++.h>
using namespace std;
void I2S(int x,string&str){stringstream ss;if(x<=9) ss>>0;ss<<x;s>>str;
}
int nDays[13]={0,31,29,31,30,31,30,31,31,30,31,30,31};
int main(){string date1,date2;cin>>date1>>date2;int ans=0;for(int m=1;m<=12;m++){string month;I2S(m,month);for(int d=1;d<=nDays[m];d++){string day;I2S(d,day);string md=month+day;string year=md;reverse(year.begin(),year.end());string date=year+md;if(date>date1&&date<=date2) ans++;}}cout<<ans<<endl;return 0;
}[NOIP2008 提高组] 火柴棒等式
题目描述
给你 n 根火柴棍,你可以拼出多少个形如 A+B=C 的等式?等式中的 A、B、C 是用火柴棍拼出的整数(若该数非零,则最高位不能是 0)。用火柴棍拼数字 0∼9 的拼法如图所示:
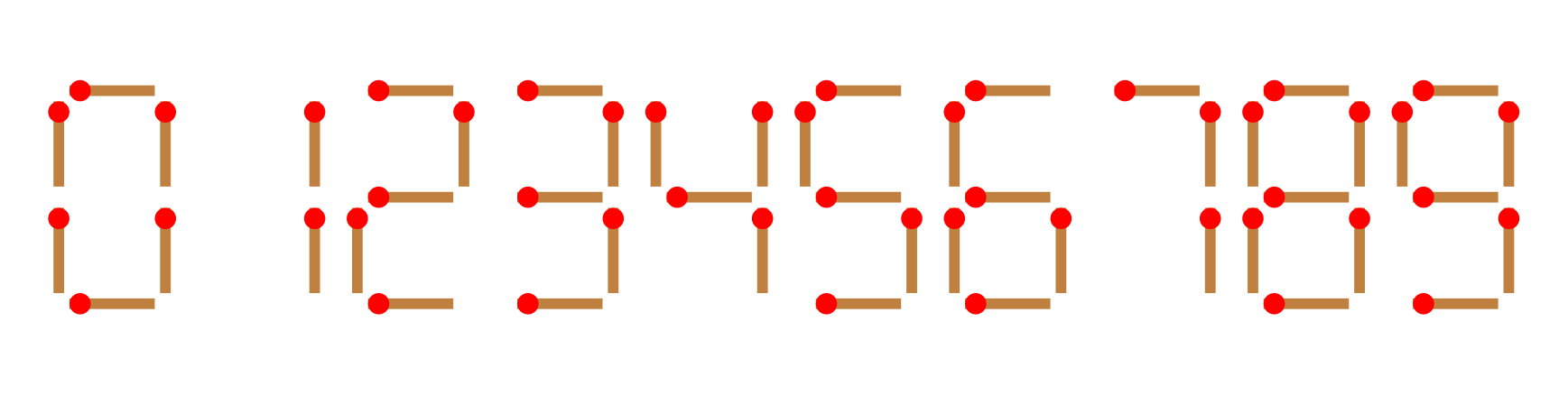
注意:
- 加号与等号各自需要两根火柴棍;
- 如果 A≠B,则 A+B=C 与 B+A=C 视为不同的等式(A,B,C≥0);
- n 根火柴棍必须全部用上。
提高组2008年第2题?考枚举?不可思议啊?那么学完例一过后,大家是不是有了亿点思路了呢?所以……请大家写写代码八!!!
预处理1
match[]数组表示单个数字i需要用几个火柴,i=0,1,2,3,4,5,6,7,8,9
所以请大家计算一下match[]数组的值。
答案是:

当然,摆的数不一定是个位数,还有可能是两位数、三位数……。于是,这个预处理还不够。
预处理2
然后,请大家打开DEV-C++,写一下matches()函数,它的功能是“给定一个整数x,x=0~999,求组成x要多少火柴”。过亿会儿公布答案。
void matches(){for(int x=0;x<N;x++){int y=x;do{cnt[x]+=match[y%10];y/=10;}while(y);}
}注意:x从0开始,要用do……while
枚举
OK!那么现在,大家想想怎么枚举的呢?我给大家一个原稿,大家试着优化一下。优化方面:1.枚举对象 2.枚举范围 3.枚举顺序
int ans=0;
for(int A=0;A<=1000;++A){for(int B=0;B<=1000;++B){for(int C=0;C<=1000;++C){if(A+B==C&&cnt[A]+cnt[B]+cnt[C]+4==n){ans++;}}}
}
cout<<ans<<endl;代码写完网上一交,唉,还真AC(All Clear)了,挺神奇的哈,这个某谷
但你想想,但凡出题老师吝啬一点,我们这代码不管什么数据,都是0分,俗称爆0。为什么呢?因为你怎么变这个数据,代码都是运行10^9次,也就是1亿次。
后面我们分两种方法详细的给大家讲讲如何优化
打表
咱们发现那,n<=24,一共就只有24种情况,咱不妨……打个表试试?所以可以提前打表,最终提交表格。有人问到,我们这表格咋填嘞。这个本地运行时间充裕,保证正确。这个办法大家尝试尝试。
减少枚举对象
对象?

啊这……其实,我们只要枚举A,B,算出C,再判断即可,所以……满满分代码来啦。
#include <bits/stdc++.h>
using namespace std;
int match[10]={6,2,5,5,4,5,6,3,7,6};
const int N=999;
int n,cnt[N];
void matches(){for(int x=0;x<N;x++){int y=x;do{cnt[x]+=match[y%10];y/=10;}while(y);}
}
int main(){cin>>n;matches();int ans=0;for(int A=0;A<=1000;A++){for(int B=0;B<=1000;B++){int C=A+B;if(cnt[A]+cnt[B]+cnt[C]+4==n){ans++;}}}cout<<ans<<endl;return 0;
}来,又又又完成一题,再来一题。
啊啊啊啊
股神
题目描述
作为股神,你的神力是能看到未来n天里每天股票的盈利或者亏损,第i天盈利x[i]元,当然如果x[i]是负数,代表亏损。一次投资可以发生在任意连续天。为了不让人发现你的神力,你必须挑选两段不重叠也不连续的投资,来掩人耳目。请计算你最多盈利多少?
这叫做“两段最大子段和问题”。考虑两个算法,①枚举4个端点 ②枚举分割点
第1中算法时间复杂度O(N^4),大家嚼的可能吗?可能。那么,我们要左右预计算了。这样吧,这道题就当作小练习,码量不多,就20多行,不要抄答案哦👍
发一个表情包分割答案

#include <bits/stdc++.h>
using namespace std;
const int N=200009;
int n,LR[N],L[N],R[N],x[N],f[N],g[N];
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>x[i];for(int i=1;i<=n;i++)f[i]=max(f[i-1],0)+x[i];L[1]=f[1];//L[]表示在1到i号的最大子段和,f[]表示以i号结尾的最大子段和 for(int i=2;i<=n;i++)L[i]=max(L[i-1],f[i]);for(int i=n;i>=1;i--)g[i]=max(g[i+1],0)+x[i];R[n]=g[n];for(int i=n-1;i>=1;i--)R[i]=max(R[i+1],g[i]);for(int i=2;i<=n-1;i++)LR[i]=L[i-1]+R[i+1];cout<<*max_element(LR+2,LR+n)<<endl;return 0;
}这题需要亿点动态规划的知识,不会的翻我主页就好了。
好了,到这里就结束了,给大家送句祝福:新年伊始,万象更新。愿所念之人,平安喜乐;愿所想之事,顺心如意。诶,大家看春晚了不?
这篇关于Peter算法小课堂—枚举优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




