2020牛客寒假算法基础集训营3——G.牛牛的Link Power II【线段树】（画图详解）

题目传送门

题目描述

牛牛有一颗大小为 $n$ 的神奇 $Link-Cut$ 数组，数组上的每一个节点都有两种状态，一种为 $link$ 状态，另一种为cut状态。数组上任意一对处于link状态的无序点对（即(u,v)和(v,u)被认为是同一对）会产生dis(u,v)的link能量，dis(u,v)为数组上u到v的距离。

我们定义整个数组的Link能量为所有处于link状态的节点产生的link能量之和。

一开始数组上每个节点的状态将由一个长度大小为n的01串给出，'1’表示Link状态，'0’表示Cut状态。

牛牛想要知道一开始，以及每次操作之后整个数组的Link能量，为了避免这个数字过于庞大，你只用输出答案对$10^9+7$取余后的结果即可。

输入描述:

第一行输入一个正整数$n(1\le n\le 10^5)$
接下里一行输入一个长度大小为n的01串表示数组的初始状态，'1’表示Link状态，'0’表示Cut状态。
接下来一行输入一个正整数$m(1\le m\le 10^5)$表示操作的数目

接下来m行，每行输入两个正整数 q , p o s ( q ∈ { 1 , 2 } , 1 ≤ p o s ≤ n ) q,pos(q \in \{ 1,2 \},1 \leq pos \leq n) q,pos(q∈{1,2},1≤pos≤n)

1. 当q=1时表示牛牛对数组的第pos个元素进行操作，将其赋值为1，保证在这个操作之前，该元素的值为0。
2. 当q=2时表示牛牛对数组的第pos个元素进行操作，将其赋值为0，保证在这个操作之前，该元素的值为1。

输出描述:

请输出m+1行表示一开始，以及每次操作之后整个数组的Link能量，为了避免这个数字过于庞大，你只用输出答案对$10^9+7$取余后的结果即可。

输入

5
00001
7
1 1
2 5
2 1
1 2
1 4
1 3
1 1

输出

0
4
0
0
0
2
4
10

题意

• 给你一个只含$0$和$1$的串，定义串的Link值为串中两个的$1$之间的距离的和，$(u,v)$和$(v,u)$被看认为是同一对，有$m$次操作，每次操作可以把串中某个$1$变为$0$，或者把某个$0$变为$1$，求一开始和每次操作后串的$Link$值。

题解

• 用线段树直接维护即可
• 区间内 $1$ 的数量 $cnt$，$Link$ 值，区间内所有的 $1$ 到区间左边界的距离之和 $dl$，区间内所有的 $1$ 的区间右边界距离之和 $dr$。
• 查询的时候只要输出 $tree[1].Link$ 即可，修改时只需改变区间内 $cnt$，然后合并区间
• 现在我们考虑合并区间
  
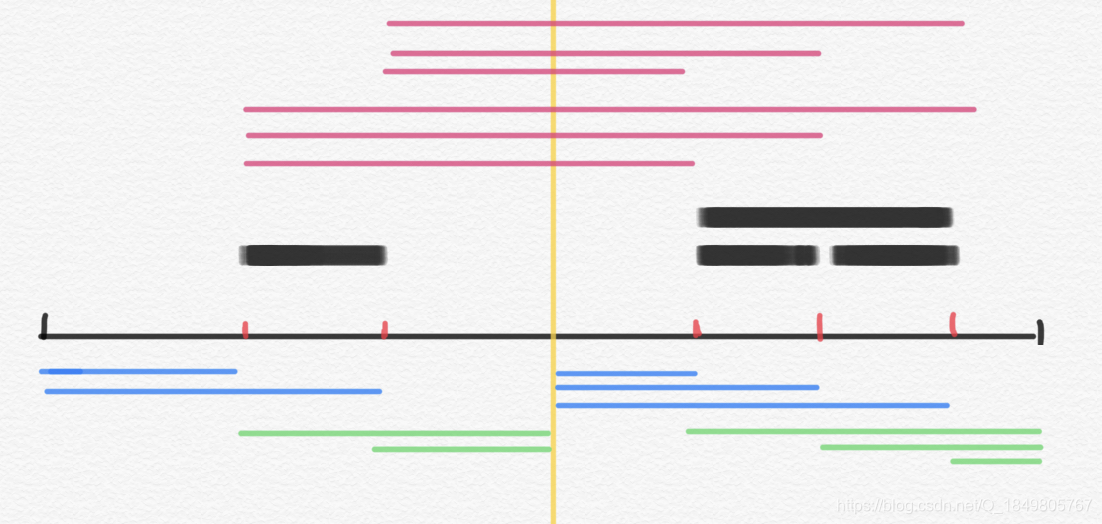
  如图，考虑这样的普遍情况，我们有左区间、右区间，现在要将两区间合并。
  合并之后的 $Link$ $=$ $左区间内部的Link+右区间内部的Link+跨越中间mid（黄线）的贡献(紫线)$
  那么我们只需要得到 $紫线$ 就可以求得合并的 $Link$。
  我们将 $紫线$ 分成左右两部分来看，很容易发现，$紫线左部分$ $=右.cnt\ast 左.dr$,同理，$紫线右部分$ $=左.cnt\ast 右.dl$。
• 但是这样并不是最终答案，考虑下图
  
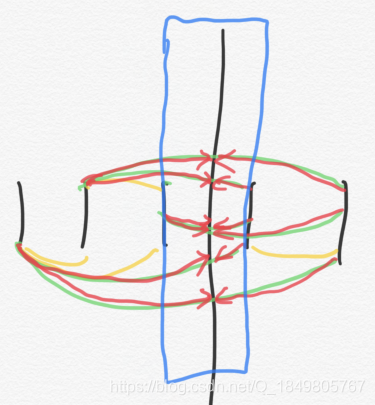
  这是数据 $11111$ 的图，经过我们的分析，显然上述合并方程是正确的，但是忽略了一个问题，就是 $dl$ 和 $dr$ 的取值问题。
  我们定义 $dl:区间内所有的1到区间左端点的距离和$，但是对于左端点如果是1的时候，这个距离是没有被计算到的（如上图）
  当我们合并的时候，正常来说 $右.dl=1+2=3$，但实际上，第四个1到左端点的距离是0，我们得到的 $右.dl=2$
  那我们发现，缺少的就是蓝色框中的长度，容易发现，这部分是 $左边所有1$ 和 $右边所有1$ 共同贡献的，而整个蓝框的长度就是1个单位长度，那么缺少的是 $条数\ast 1=条数$。那么我们就可以得到 $缺少的部分=左.cnt\ast 右.cnt\ast 1$，计算 $合并Link$ 的时候加上这部分即可。
• 至此，这道题就算解决完了，注意取模，不要爆精度即可。

AC-Code

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 7;
const int mod = 1e9 + 7;string s;
struct Node {int left, right;ll Link, dl, dr, cnt;
};
struct Segment_Tree {
#define mid ((tree[rt].left + tree[rt].right) >> 1)Node tree[maxn << 2];void PushUp(int rt) {tree[rt].cnt = tree[rt << 1].cnt + tree[rt << 1 | 1].cnt;int t = (tree[rt << 1].cnt * tree[rt << 1 | 1].dl + tree[rt << 1 | 1].cnt * tree[rt << 1].dr) % mod; // 跨越两个区间mid的贡献tree[rt].Link = tree[rt << 1].Link + tree[rt << 1 | 1].Link + t + tree[rt << 1].cnt * tree[rt << 1 | 1].cnt;tree[rt].dl = tree[rt << 1].dl + tree[rt << 1 | 1].dl + tree[rt << 1 | 1].cnt * (tree[rt << 1].right - tree[rt << 1].left + 1) % mod;tree[rt].dr = tree[rt << 1].dr + tree[rt << 1 | 1].dr + tree[rt << 1].cnt * (tree[rt << 1 | 1].right - tree[rt << 1 | 1].left + 1) % mod;}void build(int rt, int l, int r) {tree[rt].left = l;tree[rt].right = r;if (l == r) {tree[rt].dl = tree[rt].dr = tree[rt].Link = 0;if (s[l] == '1')	tree[rt].cnt = 1;else 	tree[rt].cnt = 0;return;}build(rt << 1, l, mid);build(rt << 1 | 1, mid + 1, r);PushUp(rt);}void update(int rt, int pos, int val) {if (tree[rt].left == tree[rt].right) {tree[rt].cnt = val;return;}if (pos <= mid)	update(rt << 1, pos, val);else	update(rt << 1 | 1, pos, val);PushUp(rt);}
#undef mid
};
Segment_Tree st;
int main() {int n;	while (cin >> n) {cin >> s;	s = " " + s;st.build(1, 1, n);cout << st.tree[1].Link % mod << endl;int m;	cin >> m;while (m--) {int q, pos;	cin >> q >> pos;st.update(1, pos, q == 1 ? 1 : 0);cout << st.tree[1].Link % mod << endl;}}
}