数据结构.平衡二叉树.从二叉排序树到平衡二叉树

本文主要是介绍数据结构.平衡二叉树.从二叉排序树到平衡二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

正在上数据结构的课程
感觉平衡二叉树很有对称的美感
所以决定首篇博客献给平衡二叉树

平衡二叉树其实是二叉排序树的一种提升

——那么什么是二叉排序树

　　简单的讲，就是对于二叉排序树的每个节点，其左孩的值<该节点的值<右孩的值，且二叉排序树所有节点的值不重复。
如此一来，对二叉排序树进行LDR遍历的输出，便是一个递增的序列，也就是所谓的二叉“排序”树。

　　由于这种有序的特点，那么查找树中的一个元素的时候，便可以产生类似“折半查找法”的效果：
1）折半查找法要求的就是一个有序的序列，二叉排序树对应的也是一个有序的序列。
2）对于要查找的元素elem

bool FindElem(BinarySortTreeNode * node,ElemType elem)
{if(node != NULL){if(node->data == elem)//找到元素return true;else if(node->data > elem)//只需继续查找左子树return FindElem(node->LeftChild, elem);else if(node->data < elem)//只需继续查找右子树return FindElem(node->RightChild, elem);}else return false;
}

所以二叉排序树又称为二叉搜索树

——为什么说是“类似”折半查找：

　　这和二叉排序树的建立有关。由于二叉排序树的特点，新加入的元素newElem要符合二叉排序树的有序状态，所以插入的时候
　　

bool AddElem(BinarySortTreeNode*& node, ElemType newElem)
{
|   if(node != NULL)//当node非空
|   {
|   |   if(node->data == newElem)//已存在这个元素
|   |       return false;
|   |   else if(node->data > newElem)//按规则插入node左边
|   |       return AddElem(node->LeftChild, newElem);
|   |   else if(node->data < newElem)//按规则插入node右边
|   |       return AddElem(node->RightChild, newElem);
|   }
|   else//插入到node这个位置，node是引用
|   {
|   |   node = new BinarySortTreeNode;
|   |   node->data = newElem;
|   |   //处理node其他字段
|   |   return true;    
|   }
}

（root是引用传递）

就这样利用AddElem把一棵空树不断的添加元素变成一个二叉排序树，但是这个树的形状很有可能很难看——
1）首先插入了1，那么根节点的值就是1
2）再插入2，2>1，所以2插入到了根节点的右孩
3）再插入3，3>2>1，于是插入到了根节点的右孩的右孩
……
10）再插入10，10>9>……>3>2>1，于是插入到了根节点的右孩的右孩……的右孩的右孩
结果：只有一个分支从跟到叶子。

那么再对这棵树进行查找的时候，就和普通的遍历方法无异了。
原因在于
1）折半查找法是真正的“折半”，每次比较减少了一半的元素个数
2）而二叉排序树的查找仅仅是根据节点的值与elem的比较，选择了继续查找左子树还是右子树，每次虽然不必寻找另一棵子树，但另一棵子树也许未必包含很多元素，所以并不一定达到了”折半“的效果。

——这个时候，就该平衡二叉树登场了

平衡二叉树的思想（AVL）

简单的说就是保证每个节点的左右子树差距不是很大，如此一来在查找的时候舍弃了另一棵子树也就近似于“折半”了。

于是为每个节点添加了一个字段int balance
balance = 左子树深度 - 右子树深度
（两个数相减的值可以作为这两个数的一种比较）
1）当balance的绝对值<=1的时候就认为“差距不大”，为“平衡状态”
2）当balance的绝对值>=2的时候就认为“差距过大”，为“不平衡状态”
3）定义二叉平衡树：所有节点的balance的绝对值均<=1

每次添加/删除一个元素
势必会影响到某处的深度
进而影响到balance的值
就有可能使得操作之后的二叉树不再处于平衡状态

解决办法就是：
每次添加/删除一个元素后，根据balance的变化，把不平衡的地方进行某种所谓的“旋转”使得重新变成平衡的状态。
每次的添加/删除操作都是针对一个平衡的二叉树，如果操作完成后不平衡了则重新整理成平衡状态，这就保证了二叉树时刻处于平衡状态。

平衡二叉树的旋转原理

对于一棵已经处于平衡状态的二叉树，添加/删除一个元素对其的平衡状态的影响实际上非常有限。
由于原先的balance只有三个值“0，1，-1”，所以一个元素的影响只有使得“-1变成-2”或“1变成2”才可以破坏平衡。

例如：
图1：一个平衡的二叉树

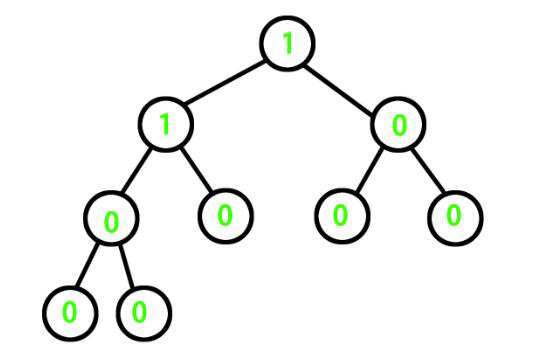
图2：添加了一个元素（深色阴影）后不再平衡，可以看到其产生的影响一路向上破坏了很多节点的平衡

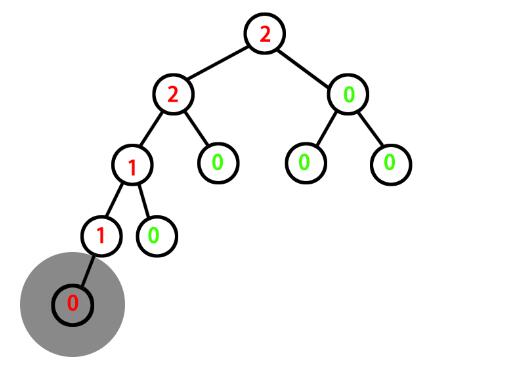
图3：应该如何旋转呢，先标记一下元素，有两个不平衡的节点A和B，我们真正旋转的部分是“浅色阴影部分”

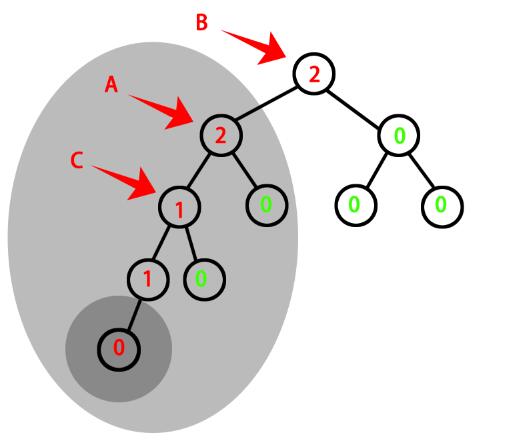
图4：经过旋转（修改指针域）（乱乱哒）

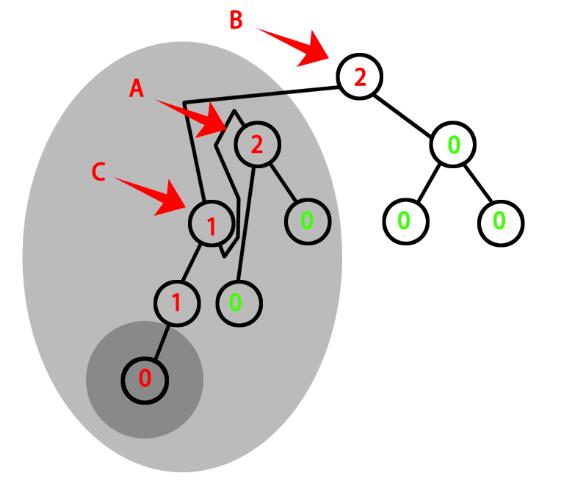
图5：恢复到平衡状态（B节点只需要修改指针域，B以上的节点完全不需要改变）

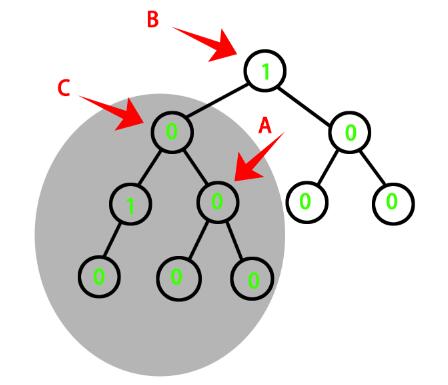
——可以看到我们最需要的节点是“从新添加的节点开始向上寻找第一个不平衡的节点”，也就是图中的A，以这个节点为根节点的子树进行旋转，并改变需要A和C的balance值。
——A子树作为B的右子树，旋转后A子树的根节点变成了C，因此B的右孩也需要改变成C，所以我们还需要知道A的父节点是哪个。
——但A的父节点B只有右孩需要改变，其balance值并没有改变（因为B的右子树的深度并没有改变），这也是旋转的魅力之一，使得新添加元素的影响被限制在了”浅色阴影部分“。

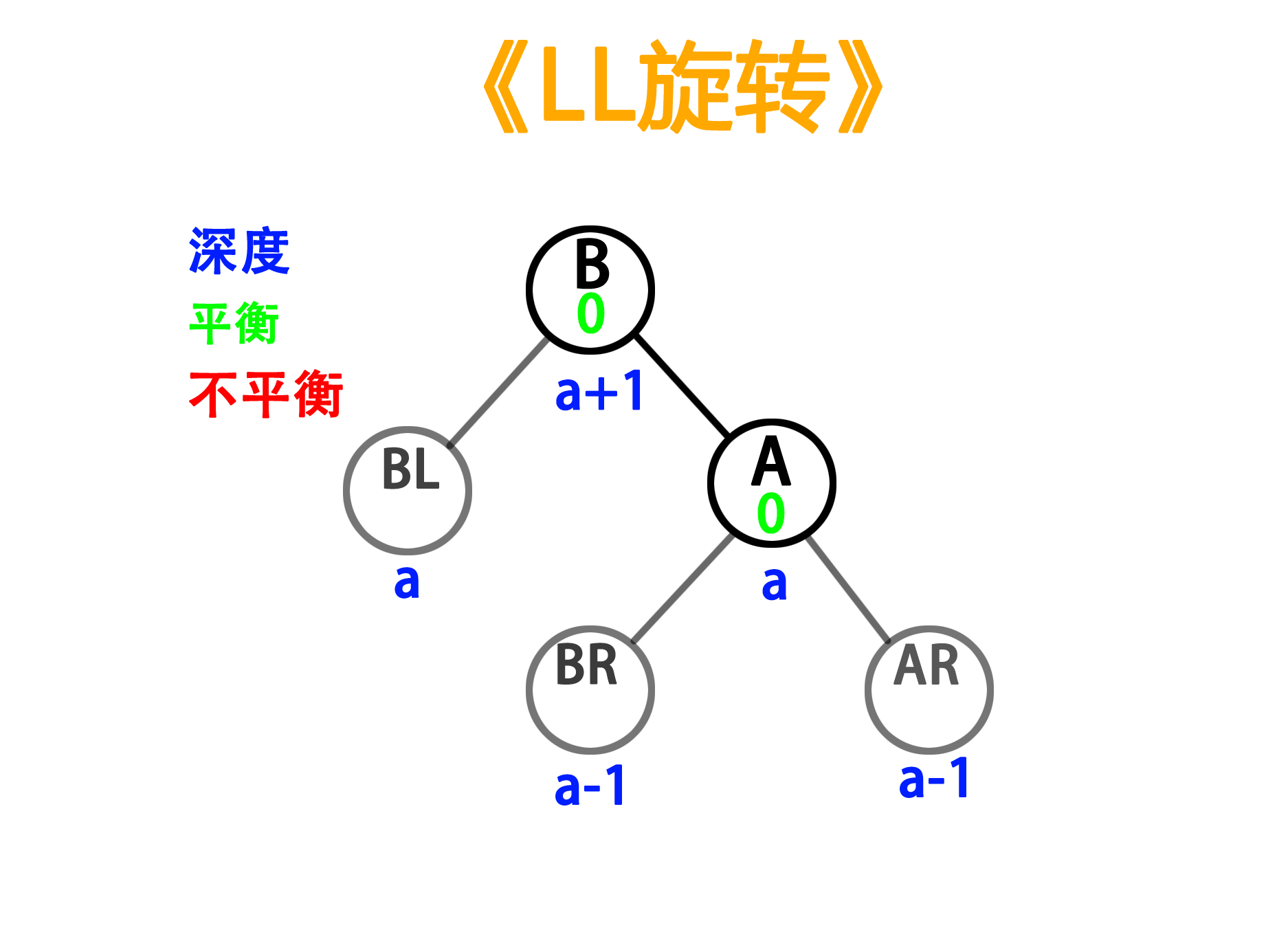
以上的情况称为”LL型旋转“。

四种旋转情况

——旋转针对的是”以第一个不平衡的节点为根“的子树，而且这种不平衡的状态是在平衡状态的基础上由一个元素的影响产生的。
——所以这样的不平衡状态情况有且仅有四种，其他的情况均不可能是在平衡状态的基础上由一个元素的影响产生的。

1）LL型旋转
——旋转前

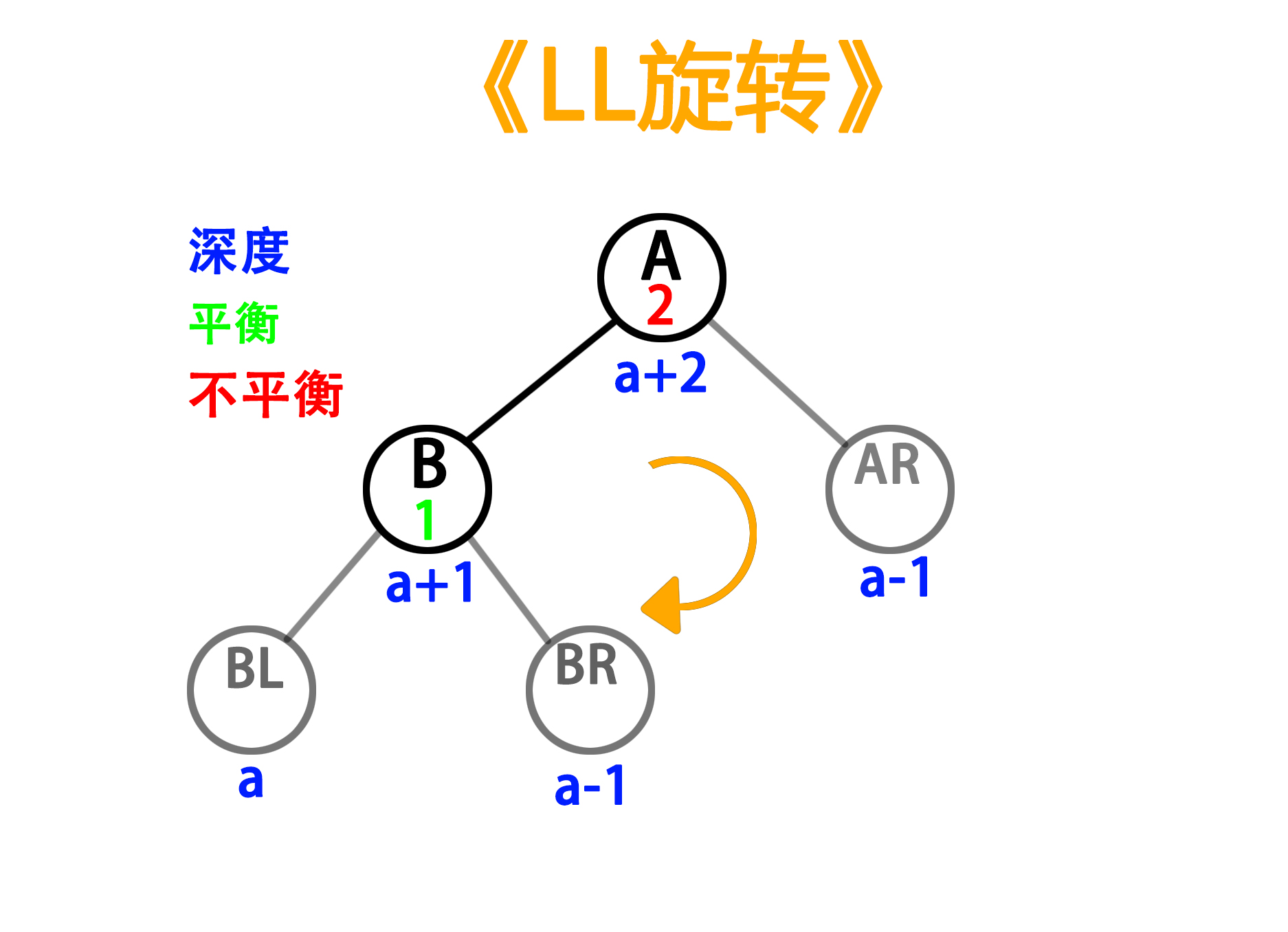
——旋转后

2）LR型旋转，这里因为需要用到第三个C节点，所以有两balance值的情况
——旋转前

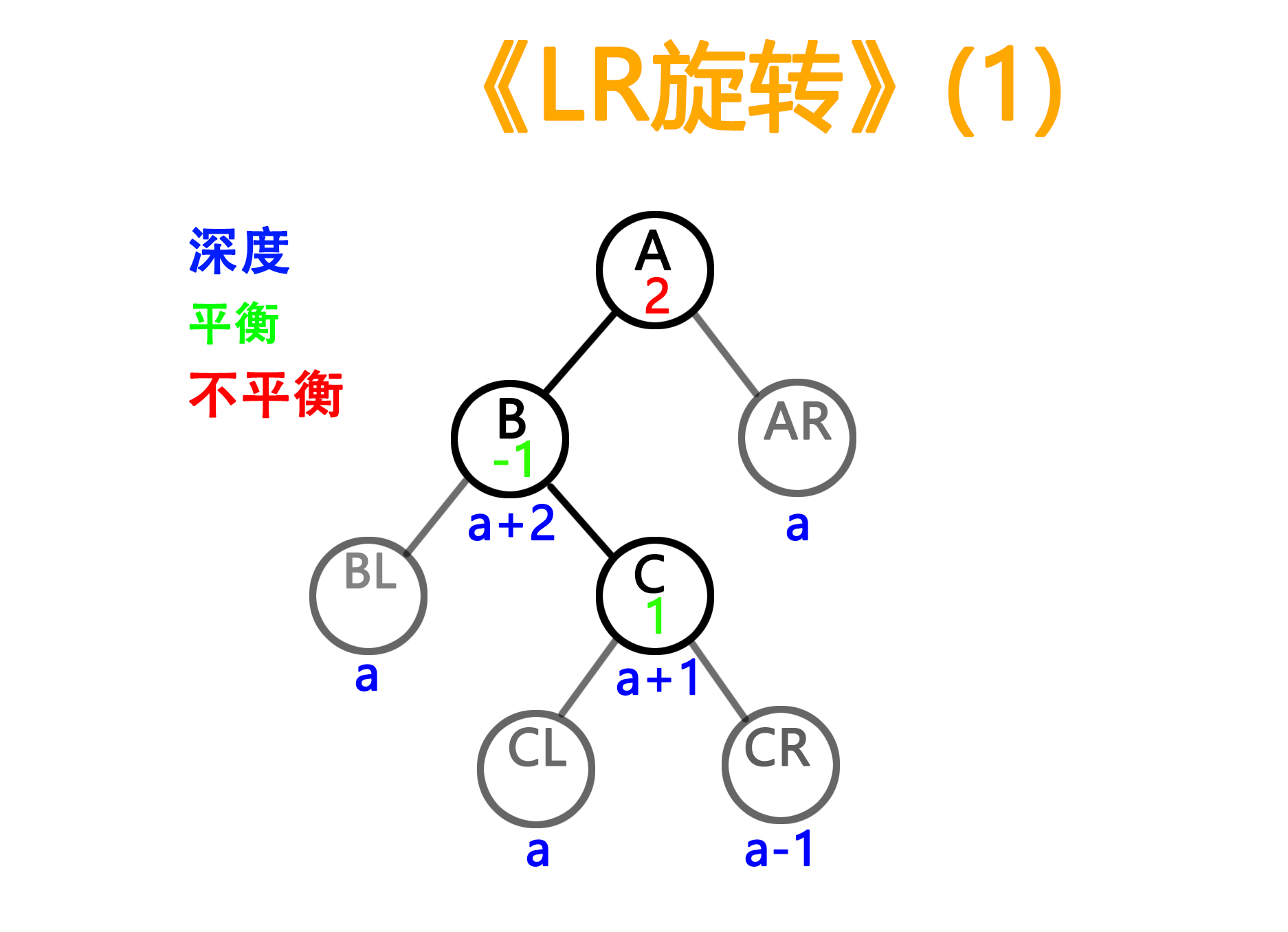
——旋转后

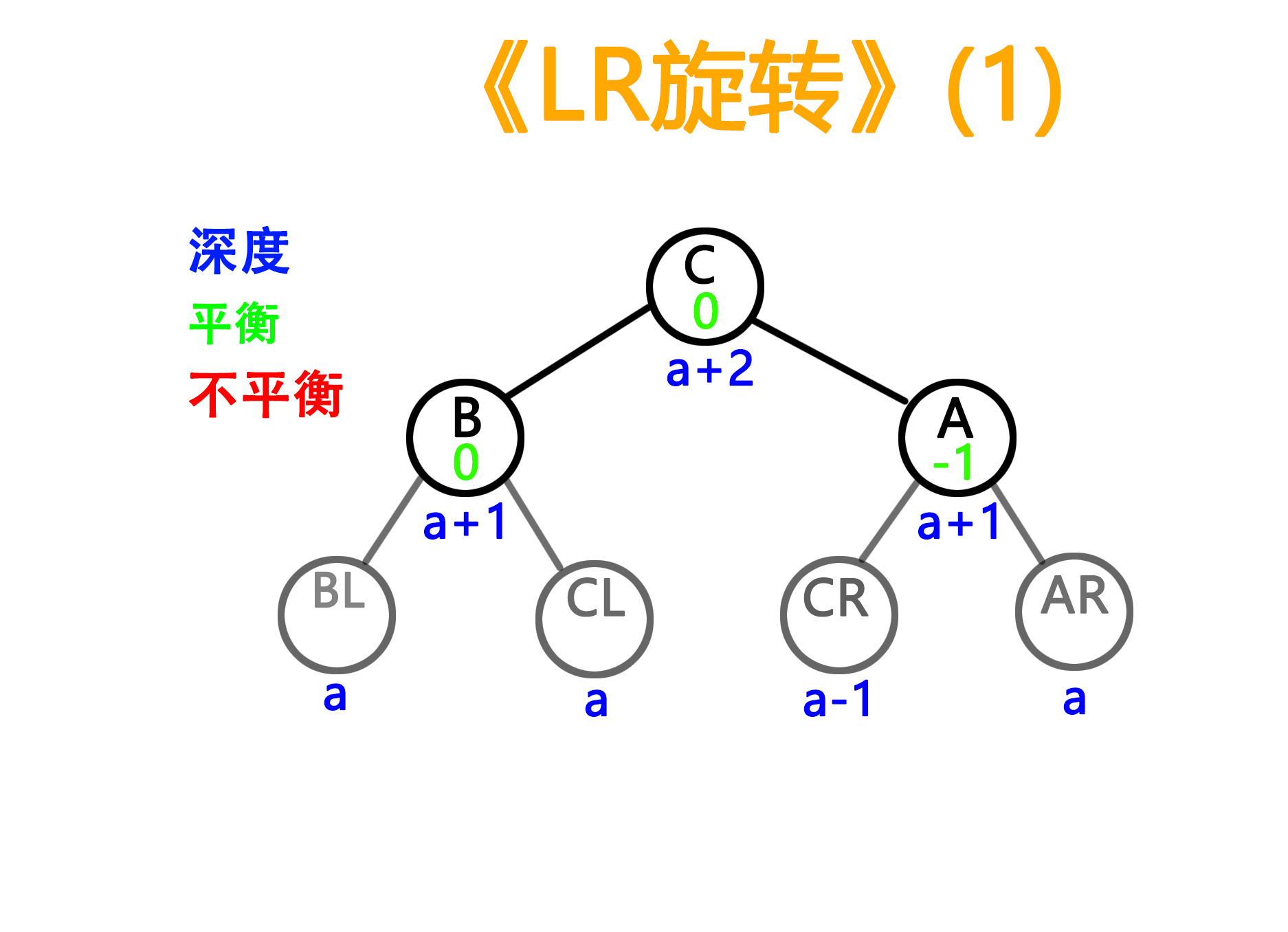
——旋转前

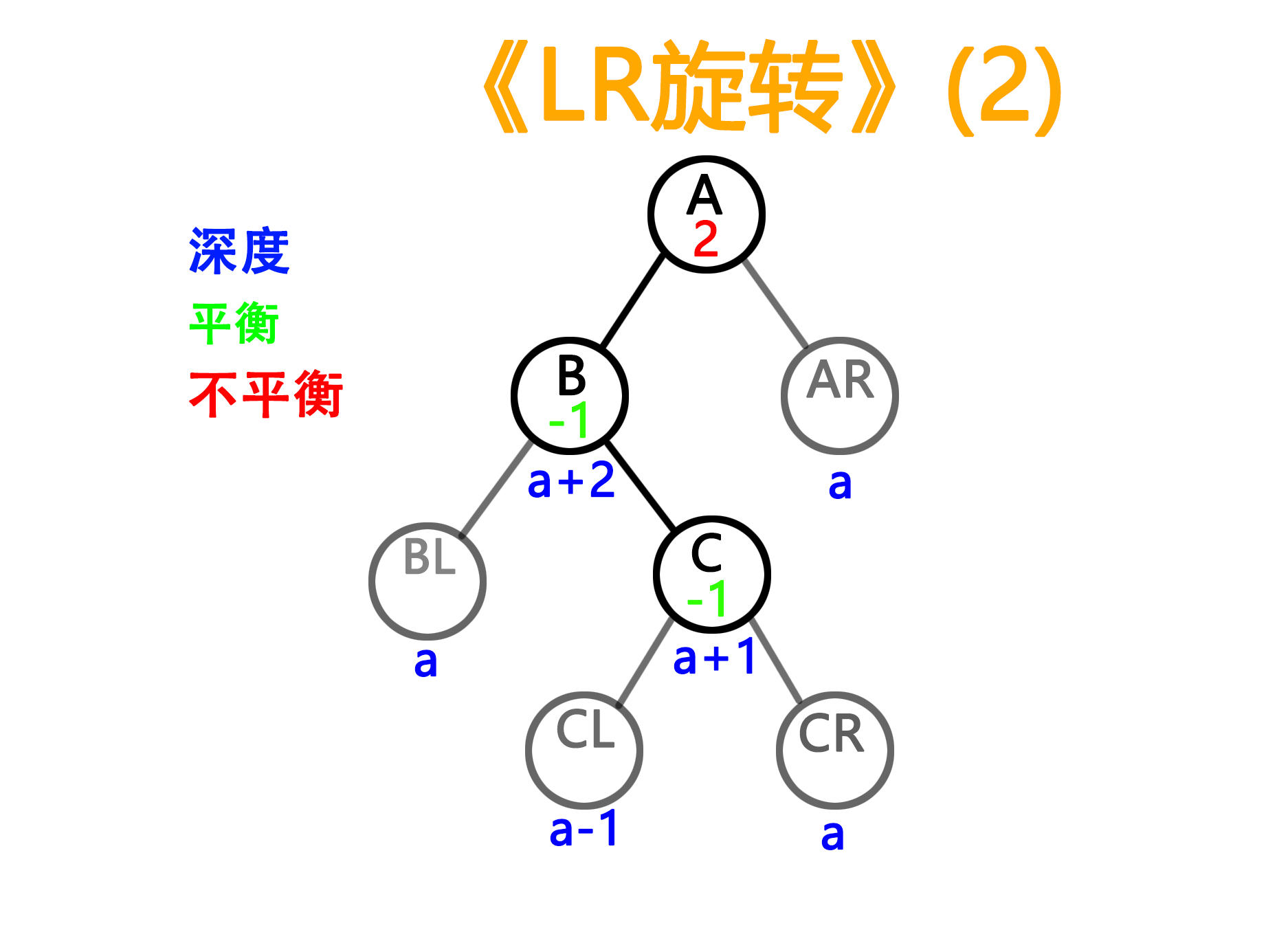
——旋转后

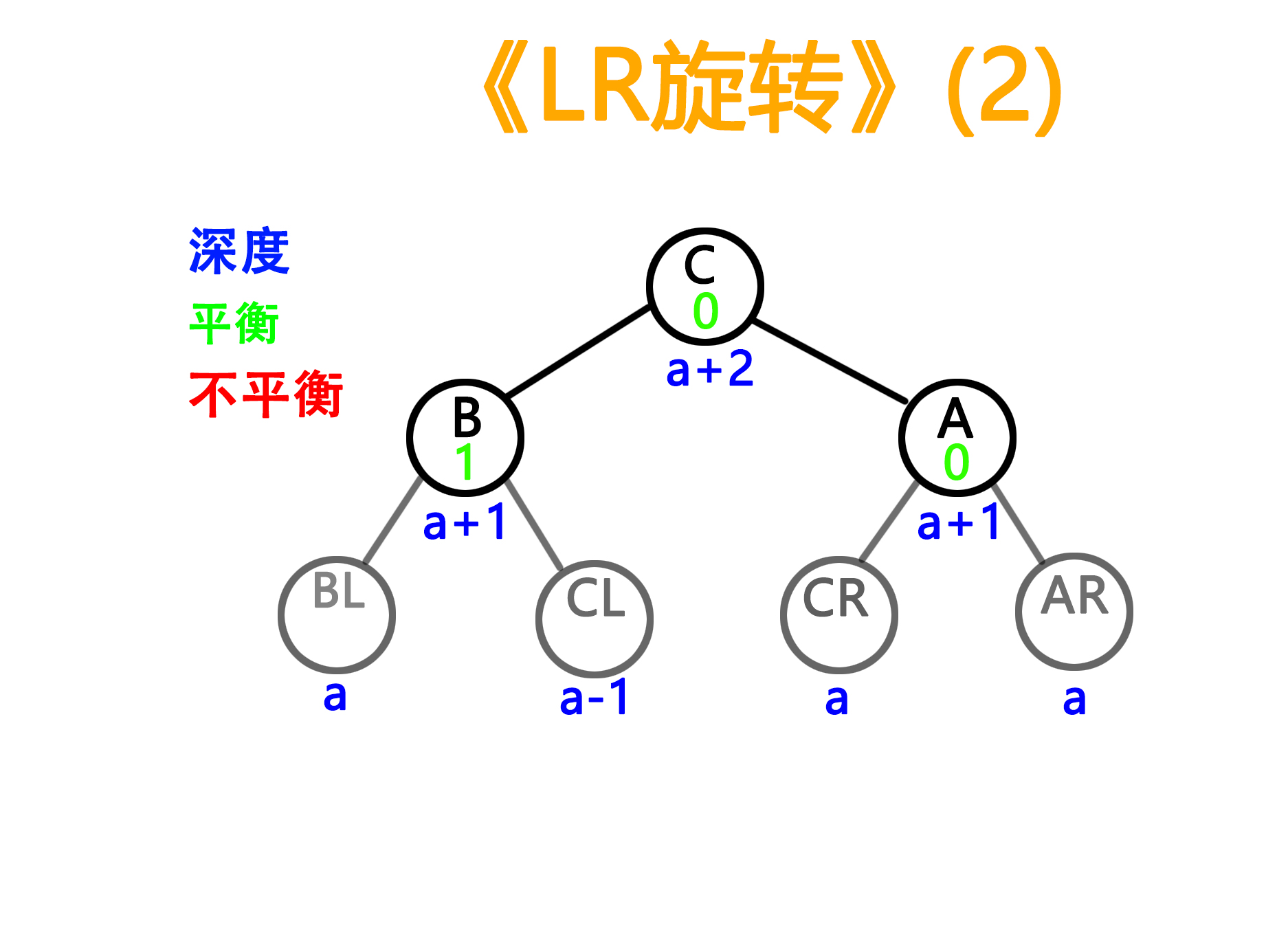
3）RR型旋转（与LL对称）
——旋转前

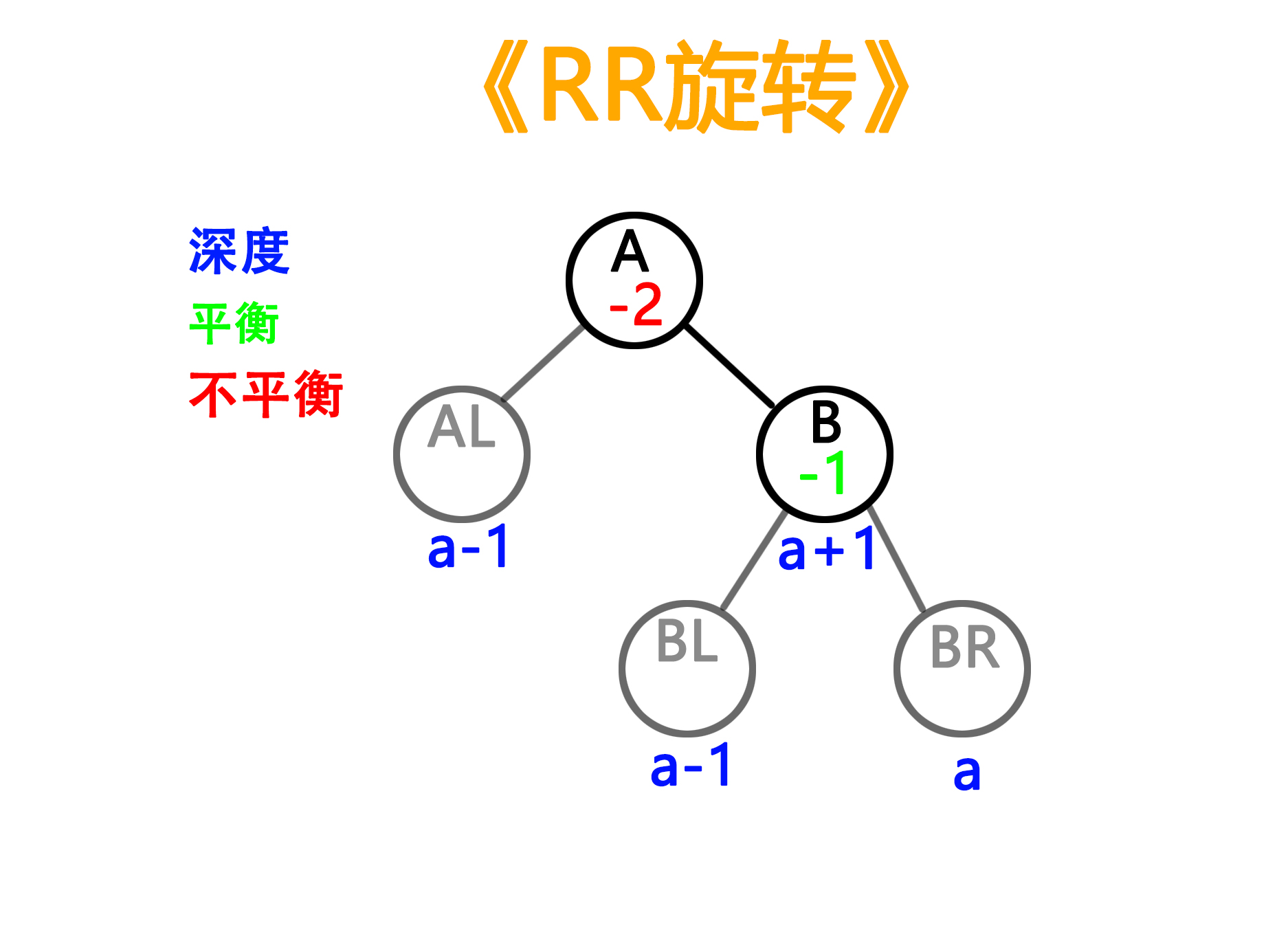
——旋转后

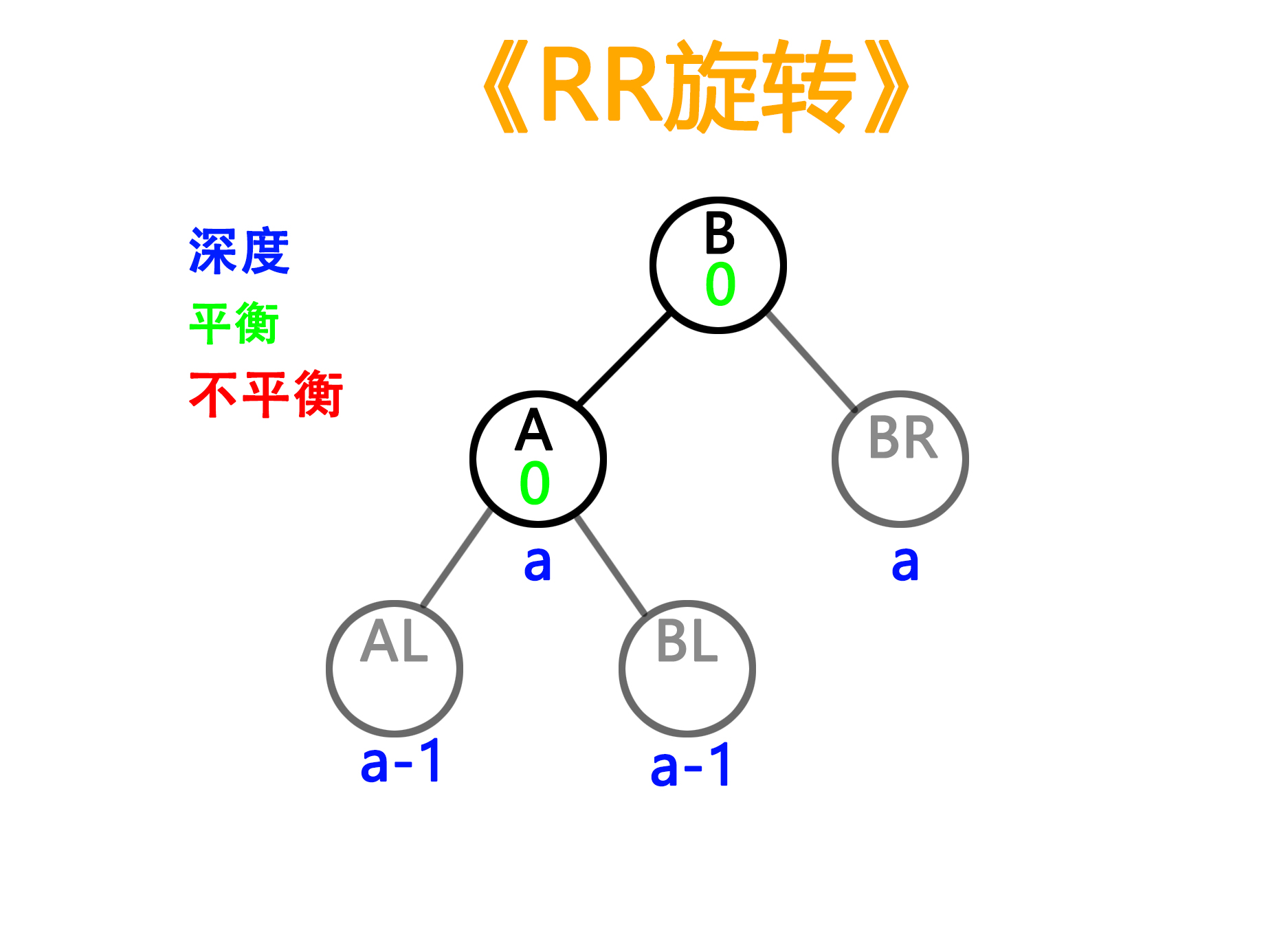
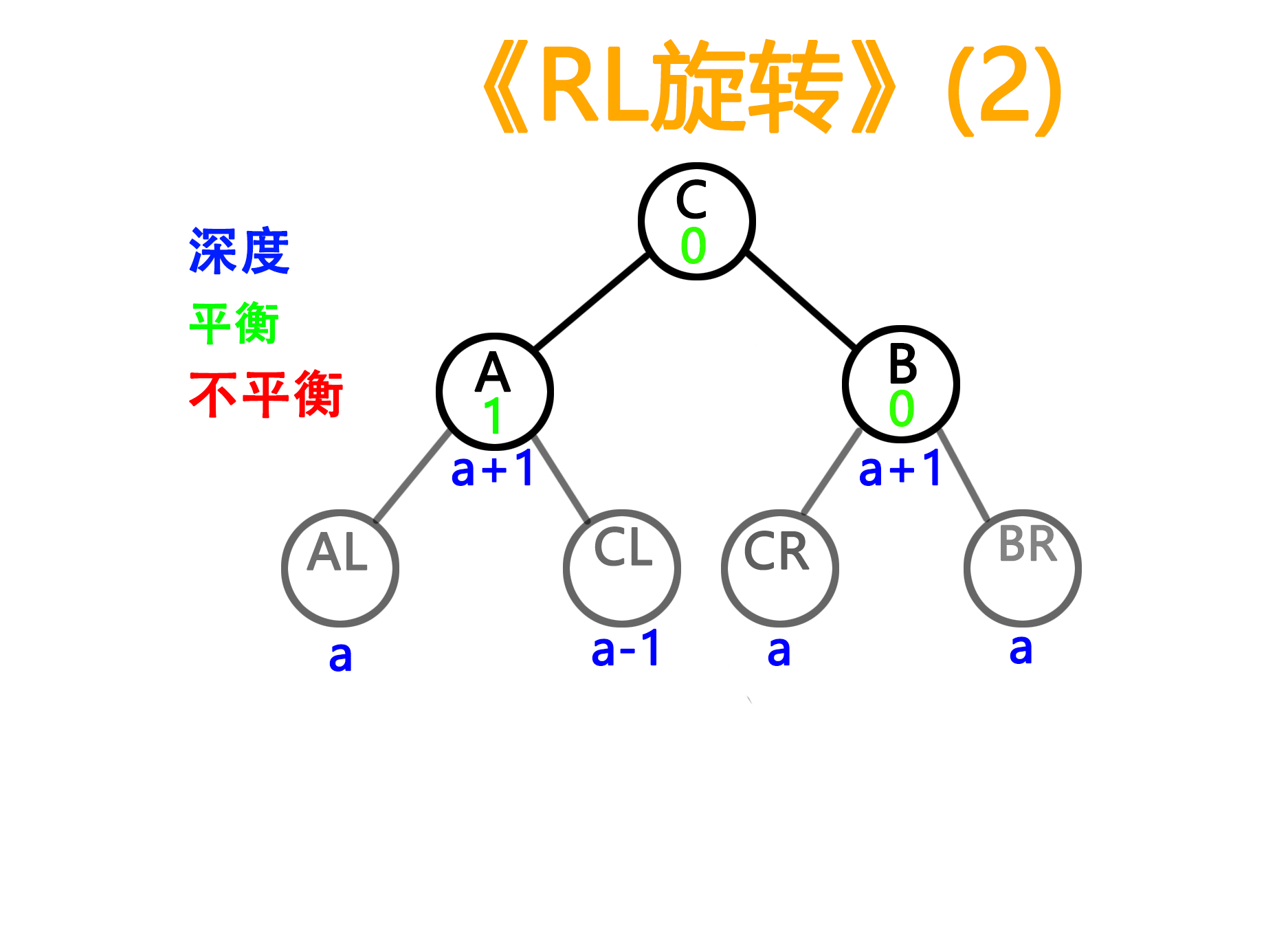
4）RL型旋转（与RR对称，同样两种balance值的情况）
——旋转前

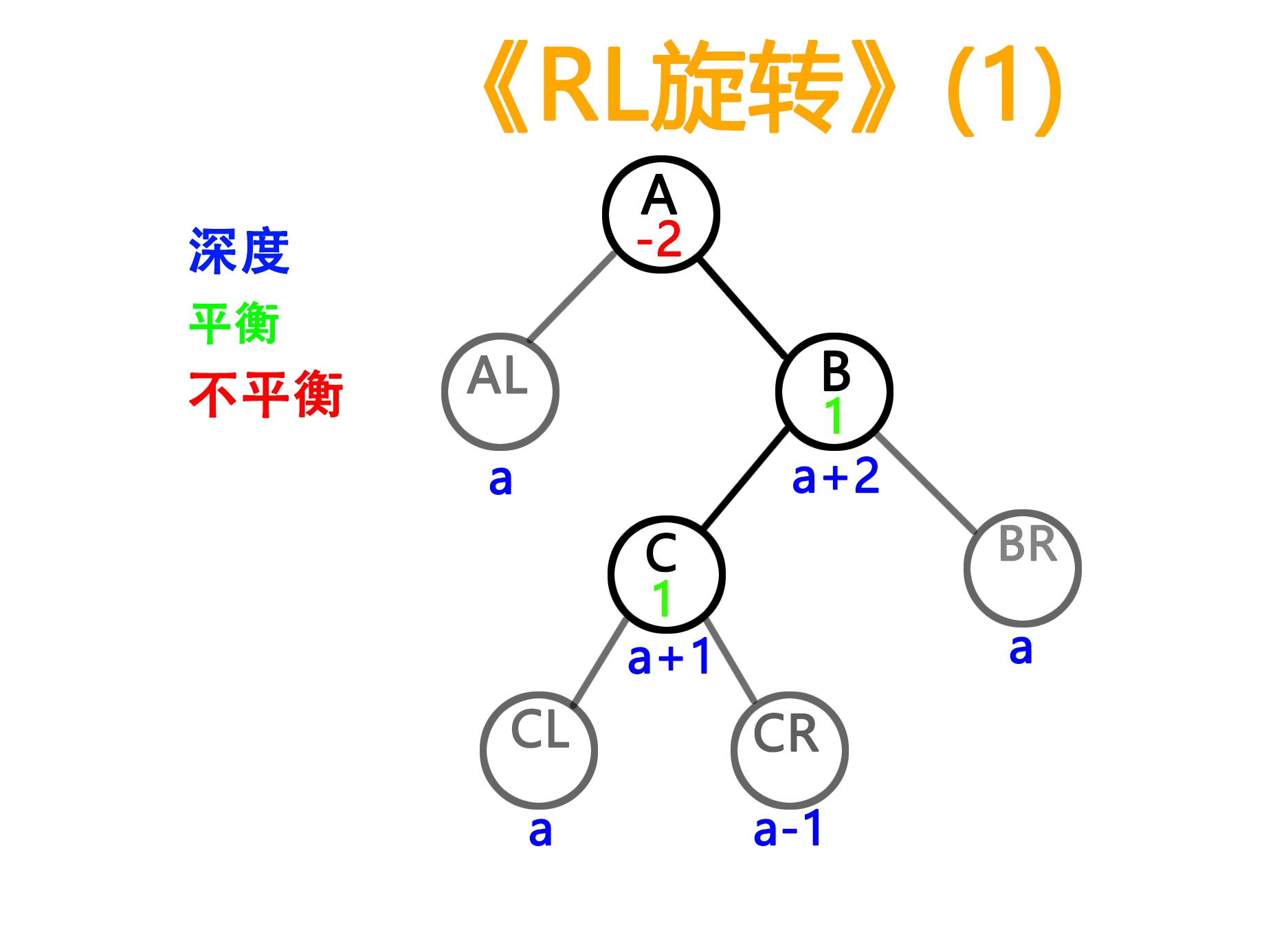
——旋转后

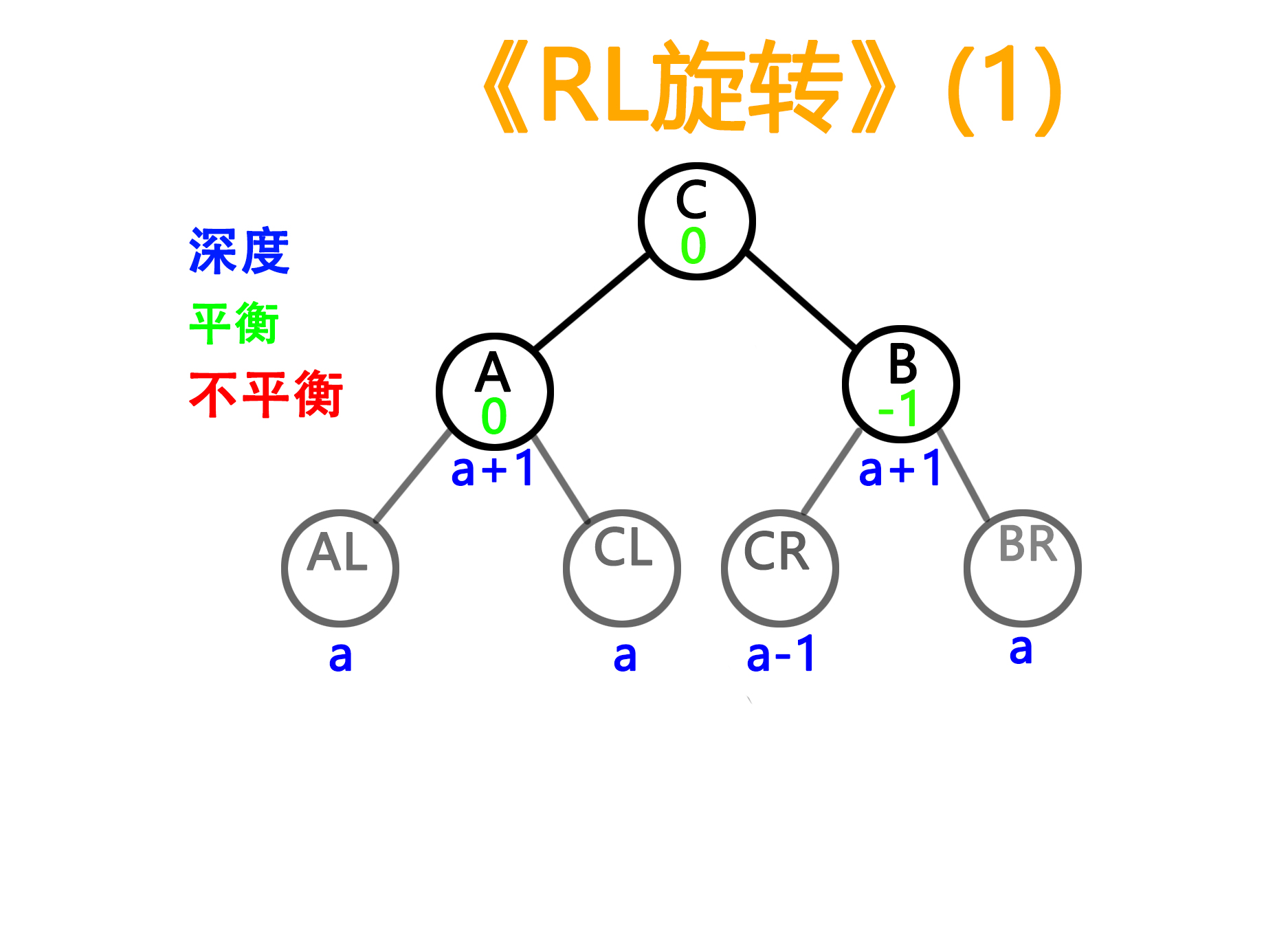
——旋转前

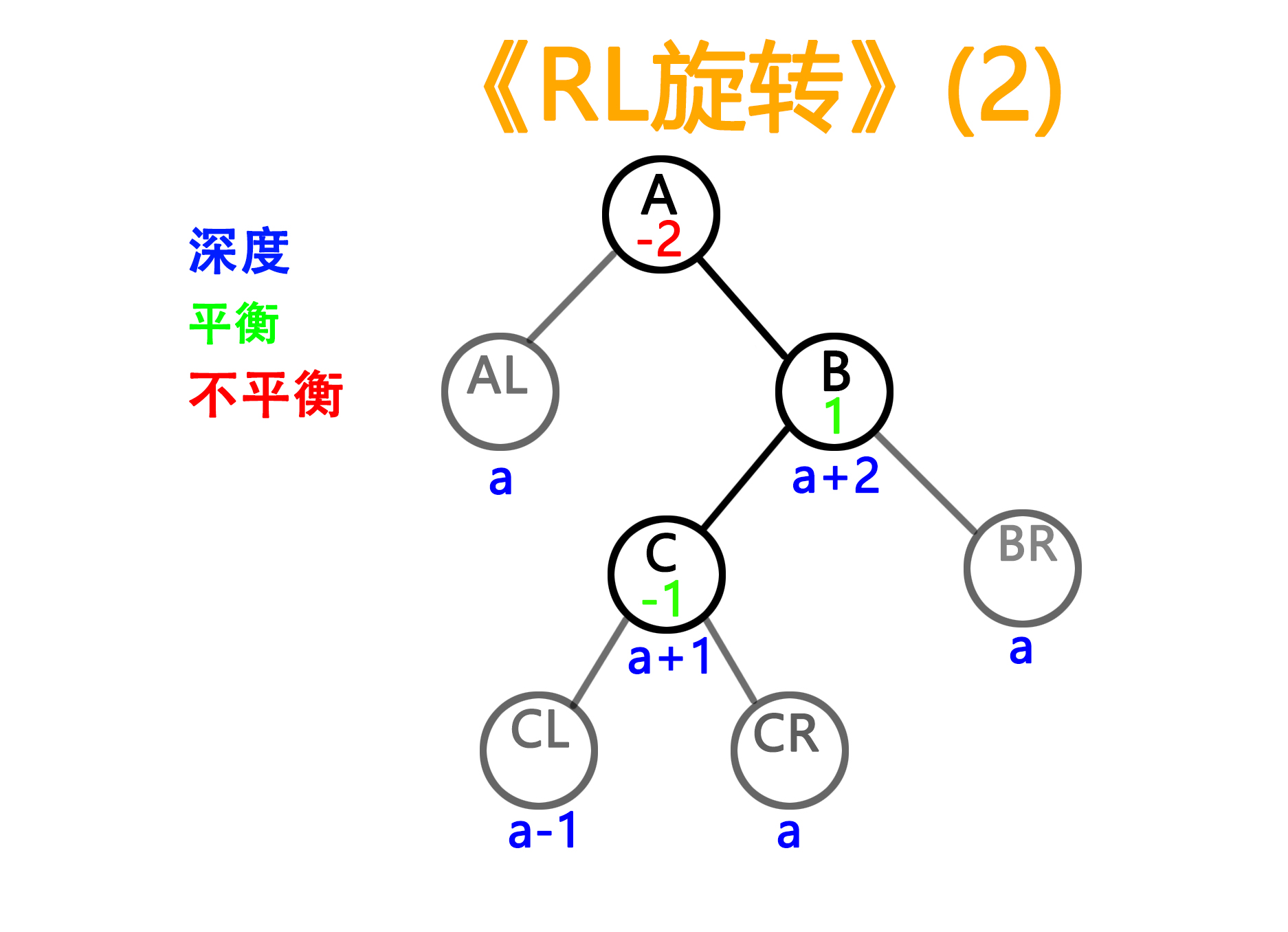
——旋转后

对称的特点可以更好的体现在代码上，3）和4）的代码只需要把1）和2）的代码里的LefiChild和RightChild交换就可以得到。

部分代码实现

先定义树节点结构体TreeNode，要求类型T为基本类型或重载了”>”“<”“==”

template<typename T>
struct TreeNode
{T data;int balance;TreeNode *parent;TreeNode *LeftChild;TreeNode *RightChild;
};

定义一个旋转函数对旋转情况进行分类，只需要传入指向首个不平衡节点的指针即可

    void Swing(TreeNode<ElemType>*p){if (p->balance == 2){if (p->LeftChild->balance == 1)//LL型旋转SwingLL(p, p->LeftChild);else if (p->LeftChild->balance == -1)//LR型旋转SwingLR(p, p->LeftChild, p->LeftChild->RightChild);}else if (p->balance == -2){if (p->RightChild->balance == -1)//RR型旋转SwingRR(p, p->RightChild);else if (p->RightChild->balance == 1)//RL型旋转SwingRL(p, p->RightChild, p->RightChild->LeftChild);}}

LL旋转的实现

    void SwingLL(TreeNode<ElemType>*A, Tree     Node<ElemType>*B){TreeNode<ElemType> *parent = A->parent;if (parent != NULL){if (IsLeftChild(A)) parent->LeftChild = B;else parent->RightChild = B;}else root = B;A->LeftChild = B->RightChild;if (B->RightChild != NULL)B->RightChild->parent = A;B->RightChild = A;A->parent = B;B->parent = parent;A->balance = 0;B->balance = 0;}

LR旋转的实现

    void SwingLR(TreeNode<ElemType>*A, TreeNode<ElemType>*B, TreeNode<ElemType>*C){A->LeftChild = C;C->parent = A;B->RightChild = C->LeftChild;if (C->LeftChild != NULL) C->LeftChild->parent = B;C->LeftChild = B;B->parent = C;TreeNode<ElemType> *parent = A->parent;if (parent != NULL){if (IsLeftChild(A)) parent->LeftChild = C;else parent->RightChild = C;}else root = C;A->LeftChild = C->RightChild;if (C->RightChild != NULL) C->RightChild->parent = A;C->RightChild = A;A->parent = C;C->parent = parent;if (C->balance == 1){C->balance = 0;B->balance = 0;A->balance = -1;}else{C->balance = 0;B->balance = 1;A->balance = 0;}}

代码中出现的root，表示根节点，由于原本我的函数写在类内，类内又有一个root指针作为二叉树的根节点。

——END

这篇关于数据结构.平衡二叉树.从二叉排序树到平衡二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---