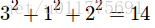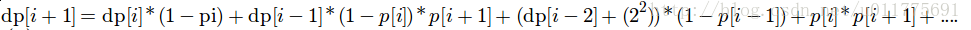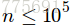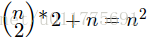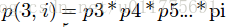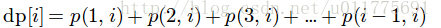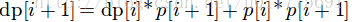CF 235B Let's play Osu! 概率DP 好题

题意：

给n个位置，给出1-n上每个位置出现O的概率pi，记分规则如下，连续的x个O记为x^2分，求和，如 XXOOOXOXOOXX得分为

求得分的期望

 

 

思考一下，我们能比较容易地得出O（n^2）的方法

令dp[i]为前i的得分期望

那么

显然这题

 

 

 

 

考虑一下变换记分的方式

我们有

那么记分方式就变为

一段连续的O，有多少对O×2+O的个数

一对O可以贡献2分

 

现在得分来源变为两个地方

一对O（2分），和单个O（1分）

 

我们知道

期望=概率×收益

我们找到每个对O的概率×2

再找到单个O×出现概率

求和即是期望得分

 

对于某一个点i

有(1,i) (2,i) (3,i) (4,i)...(i-1,i)这些对O，每个概率即是从左到右连乘，比如

令这些概率和为dp[i],即

这样我们有递推关系

对i+1点来说，

 

dp求和即是所有对O出现的概率之和×2

+

单个O出现的概率×1

求得的即是期望分数

 

 

 

记住：

1.期望=概率*收益

2.利用C(n,2)+n=n^2等变换实现记分变换

 

 

 

#include<cstdio>

const int maxn=1e5+10;

double p[maxn];
double dp[maxn];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf",&p[i]);
    }
    dp[1]=0.0;
    double ans=0.0;
    for(int i=2;i<=n;i++)
    {
        dp[i]=dp[i-1]*p[i]+p[i-1]*p[i];
        ans+=2.0*dp[i];
    }
    for(int i=1;i<=n;i++)
        ans+=p[i];
    printf("%.15f\n",ans);

    return 0;
}