诚实大多数下抵抗恶意敌手的高效安全三方计算

ABSTRACT

本文提出一个新的恶意安全下诚实多数的关于任意函数的安全三方计算协议。该工作基于Araki 等人（CCS'2016）提出的半诚实协议，改进为恶意敌手、诚实大多数模型下的Correct with Abort 安全三方计算协议。主要是通过构造Beaver乘法元组来对门电路进行验证，从而达到计算正确的目的。不同于TinyOT和SPDZ，本文基于cut-and-choose范式来保证元组被正确构造，同时提出新的可被用在相关cut-and-choose的组合分析方法。论文原文链接如下：

https://link.springer.com/chapter/10.1007/978-3-319-56614-6_8

INTRODUCTION

安全计算的设定中，要求一组互不信任的多方联合计算一个约定的函数得到输出，而不泄漏关于输入的任意信息。安全计算协议要求保证1）Privacy；2）Correctness。为刻画安全性，对敌手的行为分为半诚实和恶意两种，对敌手的数量分为诚实多数和恶意多数两种。尽管前人已有工作做到使协议满足计算安全性或者统计安全性。但是这些在半诚实或者恶意的设定下要做到统计安全性要求诚实者的数量不少于2/3。

通常有两种方法来构造通用安全计算协议的方法：

1）基于Secret-Sharing，优点是适用于低带宽，通信量少，但是交互多。

2）基于Garbled-Circuits的方法，优点是常数轮交互，适用于高延迟网络的场景，但是混乱电路带来巨大的通信开销。

本文关注在恶意安全下诚实多数的三方计算，期望在一个高速的网络环境下实现高通量（适用于一个网络设备较好的场景下，计算效率高，吞吐量大）。Araki 等人提出的半诚实协议能实现每秒70亿的AND门计算。我们的方法满足恶意安全性，在同样的实验设定下性能上可以达到50亿的门电路计算。

特别说明：本文工作仅适用于3方的情况，且仅仅是恶意安全下诚实多数情况的Correct with Abort。没有实现Fairness.

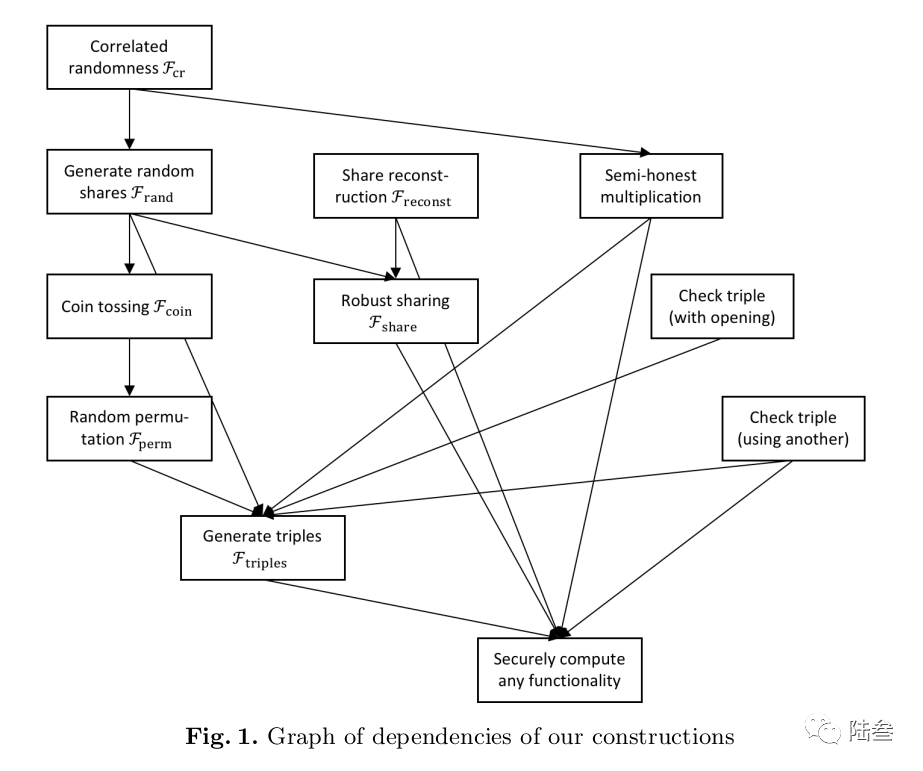
BUILDING BLOCKS AND SUBPROTOCOLS

The Secret Sharing Scheme

作为一个辅助协议，需要计算一个array的随机排列

Proposition 4： 协议2.13满足诚实多数下的恶意安全

SECURE COMPUTATION OF ANY FUNCTIONALITY

这一小节说明如何利用前面介绍的子协议计算任意函数f。

EFFICIENCY AND COMPARISON

本文与P. Mohassel et al.提出的方法（CCS‘15）进行了比较

Future Work

除了隐私保护，安全多方计算还能保证正确定、公平性和输出可达性。目前在隐私保护机器学习和安全多方计算结合的领域，业界最新的方案已经做到了诚实大多数下的输出可达性，一般是五方或者四方下的。而本次介绍的论文则是后续方案的基础部分。本专栏计划后续将逐步介绍该部分工作。

作者简介：

董业， 本科毕业于山东大学计算机科学与技术专业，目前在中国科学院信息工程研究所攻读博士学位。主要研究兴趣包括隐私保护、安全多方计算、同态加密和机器学习。知乎：酸菜鱼。