R语言阈值效应函数cut.tab2.0版发布（支持线性回归、逻辑回归、cox回归，自定义拐点）

本文主要是介绍R语言阈值效应函数cut.tab2.0版发布（支持线性回归、逻辑回归、cox回归，自定义拐点），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阈值效应和饱和效应是剂量-反应关系中常见的两种现象。阈值效应是指当某种物质的剂量达到一定高度时，才会对生物体产生影响，而低于这个剂量则不会产生影响。饱和效应是指当某种物质的剂量达到一定高度后，其影响不再随剂量的增加而增加，即产生饱和现象。这两种效应在药物、毒物、营养物质等剂量-反应关系中都有应用。
接下来聊聊RCS阈值函数是干什么用的，随便抓一篇论文给大家看看，粉丝发给我的。
L-shaped association of serum 25-hydroxyvitamin D concentrations
with cardiovascular and all-cause mortality in individuals with osteoarthritis: results
from the NHANES database prospective cohort study

我们看到它曲线拟合后直接就是一个表

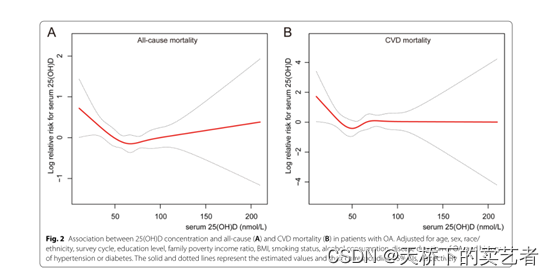
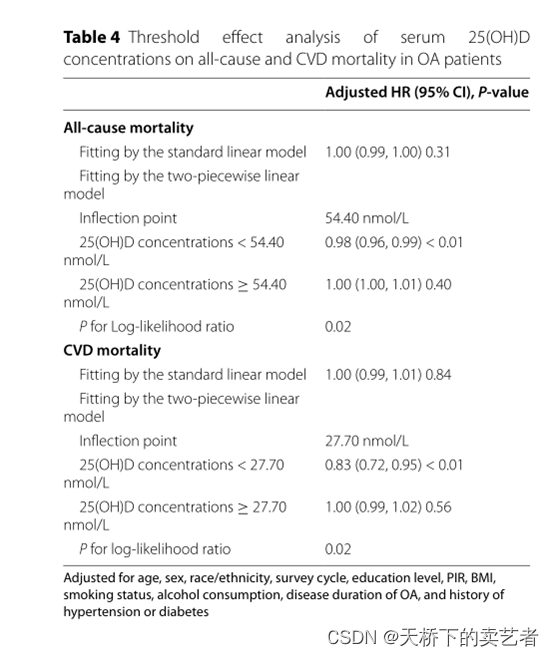
列出了25(OH)D在54.4就是转弯处前对结局影响的HR，还有在转弯后对结局影响的HR。

在既往我们在文章《cox回归RCS阈值效应函数cut.tab1.3发布》发布了自写的阈值效应函数1.3版本，反应还不错，不过1.3版本只能支持cox回归，本次发布了新的2.0版本，支持线性回归、逻辑回归、cox回归, 还有自定义拐点功能。泊松回归还不支持，目前正在开发中。下面我来演示一下，怎么通过ggrcs包做出上面论文这样一个图和自写的函数cut.tab20版来做出这样一个表
我们先导入数据和R包，数据使用ggrcs包的自带数据

library(ggrcs)
library(rms)
library(ggplot2)
library(scales)
library(cowplot)
library(survey)
dt<-smoke

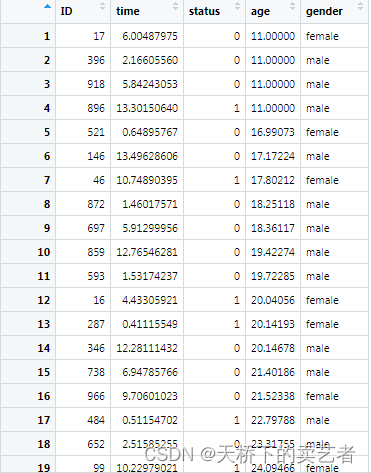
这是ggrcs包自带的吸烟数据status结局，time时间，age年龄，gender性别，我们先整理数据

dd<-datadist(dt)
options(datadist='dd')

建立模型

fit <- cph(Surv(time,status==1) ~ rcs(age,4), x=TRUE, y=TRUE,data=dt)

绘图

ggrcs(data=dt,fit=fit,x="age")

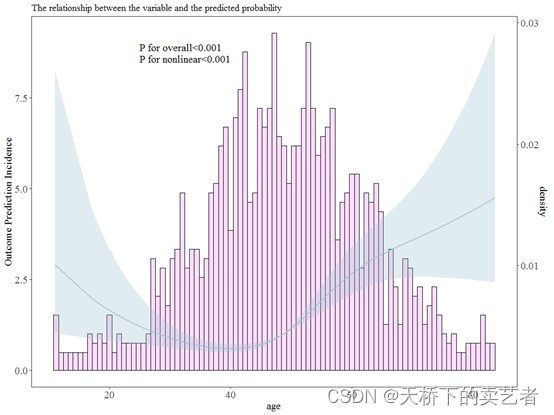
我们绘图好以后想要了解它的拐点，需要先导入我写的函数

source("E:/r/test/20final.R")

导入成功后，左侧应该生成19个函数，表明已经成功导入

接下来咱们还要建一个新的fit1和原来的fit稍微有点不一样的，这个是没有rcs函数的。自己比较一下。（划重点）

fit1 <-cph(Surv(time,status==1) ~ age,data=dt)

接下来使用cuttab函数生成拐点数据，这里注意一下，新版本和旧版本不同的是这里是cph生成生存模型，cuttab重点是没有点这个符号的。

out<-cuttab(fit1,"age",dt)

最终函数定义的拐点是38.449，新版本还支持自定义拐点设置，等会演示。这个表我要说明一下d6这里这个似然比只是表明它是不是直线，似然比大于0.05说明是个直线，并不是说直线就没有意义了（等下我再解释一下），P值这里主要看的是分段的P值。

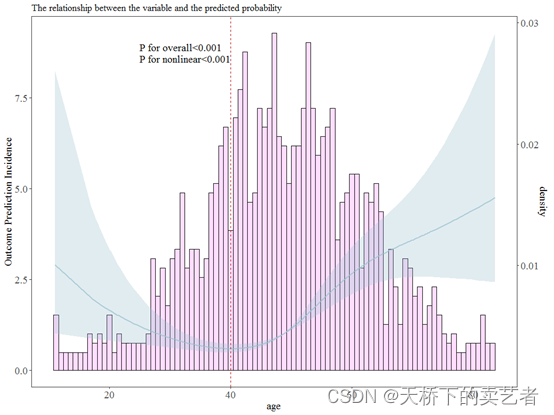
最后生成节点的虚线

p<-ggrcs(data=dt,fit=fit,x="age")
p+geom_vline(aes(xintercept=40),colour="#BB0000", linetype="dashed")

发个旧版本的操作视频

需要获取cut.tab2.0版函数的请看这篇文章：

R语言阈值效应函数cut.tab2.0版发布（支持线性回归、逻辑回归、cox回归，自定义拐点）

这篇关于R语言阈值效应函数cut.tab2.0版发布（支持线性回归、逻辑回归、cox回归，自定义拐点）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---