清北学堂-D7-T1-bst

2024-02-05 15:18

文章标签 学堂 t1 bst 清北 d7

本文主要是介绍清北学堂-D7-T1-bst，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这里写图片描述

这个题暴力给了50分，直接模拟即可。
为什么是50分呢？有些人会有这个疑问。
原因很简单，你可以模拟一下这组数据：
10
1 2 3 4 5 6 7 8 9 10
你可以发现，如果我给你你个递增序列，你的算法就会被卡到 $O(n^2)$
那这个题怎么做呢？
我这里介绍两个做法，都不是std
1.某位大佬的倍增
我们可以插入的时候更新每个点 $i$ 向下跳 $2^j$ 步的目标点，然后插入时倍增地去插入，这个算法可以过。
2.我的算法：分治+ST表
怎么做呢？
我们手玩一下样例，发现隐隐约约有点规律，可是也看不出来。
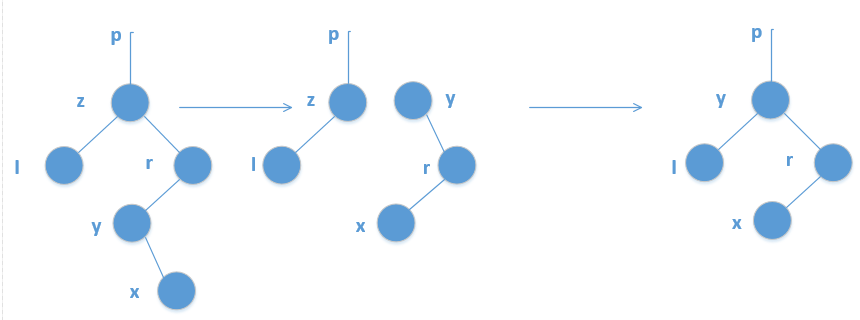
然后我就发现bst的中序遍历正好就是排序后的序列，可是为什么形态会不同呢？
我们可以发现，现在所有因素都确定了，除了插入顺序！
我们把所有数按插入顺序标号，然后按值的大小排序，再次模拟插入的过程，并把树上的节点标上插入顺序的标号，我们现在再次观察整棵树的性质，可以发现我们按插入顺序来看，整棵树就是个小根堆，这样一来算法就显而易见了。
首先读入所有数，排序。
然后我们可以每次找到一个序列中插入顺序最小的数，将其的深度设为父亲节点深度加一，然后递归地去处理左右边，这样算法的时间复杂度就是查询的时间复杂度了，我们可以用ST表，可以做到 $O(nlogn)$ 预处理， $O(n)$ 建树，然后再 $O(n)$ 累加，输出即可。
然后我就愉快地爆栈了，被卡到暴力分50，原因是我们这样递归的话在极端情况下会递归n层，然后n是 $3*10^5$ ，但是栈大小大约只有 $10^5$ ，就会爆。
处理方法也很简单，我们只要用bfs来处理就可以了，具体可以看我的代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<queue>
#define ll long long
using namespace std;
inline int read(){int x=0;char ch=' ';int f=1;while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();if(ch=='-')f=-1,ch=getchar();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;
}
int id[300001];
int n;
int a[300001];
int mp[300001];
int st[20][300001];
int Log[300001];
inline int query(int l,int r){int k=Log[r-l+1];return min(st[k][l],st[k][r-(1<<k)+1]);
}
int dep[300001];
ll ans[300001];
queue<int> ql,qmid,qr;
void solve1(){int start=query(1,n);ql.push(1);qmid.push(mp[start]);qr.push(n);while(!ql.empty()){int l=ql.front();int mid=qmid.front();int r=qr.front();ql.pop();qmid.pop();qr.pop();if(l>=r)continue;if(mid>l){int mn=query(l,mid-1);dep[mp[mn]]=dep[mid]+1;ql.push(l);qmid.push(mp[mn]);qr.push(mid-1);}if(mid<r){int mn=query(mid+1,r);dep[mp[mn]]=dep[mid]+1;ql.push(mid+1);qmid.push(mp[mn]);qr.push(r);}}
}
int main(){freopen("bst.in","r",stdin);freopen("bst.out","w",stdout);n=read();Log[0]=-1;for(int i=1;i<=n;i++){Log[i]=Log[i>>1]+1;}for(int i=1;i<=n;i++){a[i]=read();id[a[i]]=i;}for(int i=1;i<=n;i++){st[0][i]=id[i];mp[id[i]]=i;}for(int k=1;k<=19;++k){for(int i=1;i+(1<<k)-1<=n;++i){st[k][i]=min(st[k-1][i],st[k-1][i+(1<<(k-1))]);}}solve1();for(int i=1;i<=n;i++){ans[n]+=dep[i];}for(int i=n-1;i>=1;i--){ans[i]=ans[i+1]-dep[mp[i+1]];}for(int i=1;i<=n;i++){printf("%I64d\n",ans[i]);}return 0;
}