【刷题】675. 为高尔夫比赛砍树

题目

leetCode链接：https://leetcode.cn/problems/cut-off-trees-for-golf-event/

965. 为高尔夫比赛砍树

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 m x n 的矩阵表示， 在这个矩阵中：

• 0 表示障碍，无法触碰
• 1 表示地面，可以行走
• 比 1 大的数 表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 1（即变为地面）。

你将从 (0, 0) 点开始工作，返回你砍完所有树需要走的最小步数。 如果你无法砍完所有的树，返回 -1 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

示例 1：

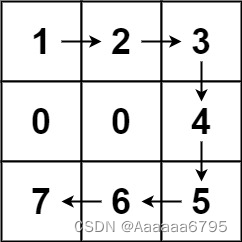
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

思路

其实是昨天的每日一题，本质上是一个BFS，相比较于一般困难难度要低一点。

因为个人BFS确实薄弱一些，还是决定写上来。

思路还是比较清晰的：首先对所有非0单元格数值做排序，然后对于每个单元格做BFS寻找到达下一个点的最短路径。如果无法到达，则返回-1 。

BFS使用队列，把每个还没有搜索到的点依次放入队列，然后再弹出队列的头部元素当做当前遍历点。

BFS总共有两个模板：

1 . 如果不需要知道遍历层数，只需要访问完所有节点，模版如下：

while queue 不空：cur = queue.pop()if cur 有效且未被访问过：进行处理for 节点 in cur 的所有相邻节点：if 该节点有效：queue.push(该节点)

2 . 如果需要知道遍历层数，如下：

level = 0
while queue 不空：size = queue.size()while (size --) {cur = queue.pop()if cur 有效且未被访问过：进行处理for 节点 in cur的所有相邻节点：if 该节点有效：queue.push(该节点)}level ++;

本题需要知道最短路径，选用模版2 。

解题

python实现

class Solution:def cutOffTree(self, forest: List[List[int]]) -> int:M = len(forest)N = len(forest[0])trees = []for i in range(M):for j in range(N):if (forest[i][j] > 1):trees.append((forest[i][j], i, j))trees.sort()preX, preY = 0, 0res = 0for height, curX, curY in trees:steps = self.bfs(forest, preX, preY, curX, curY)if steps == -1:return -1res += stepspreX, preY = curX, curYreturn resdef bfs(self, forest, startX, startY, targetX, targetY):M = len(forest)N = len(forest[0])dirs = [(0, 1), (0, -1), (-1, 0), (1, 0)]steps = 0queue = collections.deque()queue.append((startX, startY))visited = set()visited.add((startX, startY))while queue:size = len(queue)for _ in range(size):curX, curY = queue.popleft()if curX == targetX and curY == targetY:return stepsfor d in dirs:nX = curX + d[0]nY = curY + d[1]if 0 <= nX < M and 0 <= nY < N and forest[nX][nY] != 0 and ((nX, nY) not in visited):queue.append((nX, nY))visited.add((nX, nY))steps += 1return -1

golang实现

var dir4 = []struct{ x, y int }{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}func cutOffTree(forest [][]int) (ans int) {type pair struct{ dis, x, y int }trees := []pair{}for i, row := range forest {for j, h := range row {if h > 1 {trees = append(trees, pair{h, i, j})}}}sort.Slice(trees, func(i, j int) bool { return trees[i].dis < trees[j].dis })bfs := func(sx, sy, tx, ty int) int {m, n := len(forest), len(forest[0])vis := make([][]bool, m)for i := range vis {vis[i] = make([]bool, n)}vis[sx][sy] = trueq := []pair{{0, sx, sy}}for len(q) > 0 {p := q[0]q = q[1:]if p.x == tx && p.y == ty {return p.dis}for _, d := range dir4 {if x, y := p.x+d.x, p.y+d.y; 0 <= x && x < m && 0 <= y && y < n && !vis[x][y] && forest[x][y] > 0 {vis[x][y] = trueq = append(q, pair{p.dis + 1, x, y})}}}return -1}preX, preY := 0, 0for _, t := range trees {d := bfs(preX, preY, t.x, t.y)if d < 0 {return -1}ans += dpreX, preY = t.x, t.y}return
}

复杂度

时间复杂度：$\mathrm{O}(m^2\ast n^2)$,其中 m为矩阵的行数，n 为矩阵的列数。矩阵中最多有 m×n 颗树，对树的高度进行排序，时间复杂度为 $O(m\times n\times \log (m\times n))$，利用广度优先搜索两颗树之间的最短距离需要的时间为 $O(m\times n)O(m\times n)$，因此总的时间复杂为 $O(m\times n\times \log (m\times n)+m^2\ast n^2)=\mathrm{O}(m^2\ast n^2)$。

空间复杂度：$O(m\times n)$，其中m为矩阵的行数，n为矩阵的列数。矩阵中最多有 $m\times n$颗树，对树的高度进行排序，所需要的栈空间为 $O(\log (m\times n))$，利用广度优先搜索队列中最多有 $O(m\times n)$个元素，标记已遍历过的元素需要的空间为 $O(m\times n)$，因此总的空间复杂度为 $O(m\times n)$。

总结

虽然思路很简单但是代码还是看晕了。。
遇到困难睡大觉系列