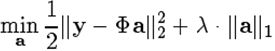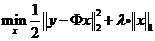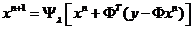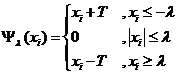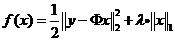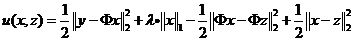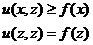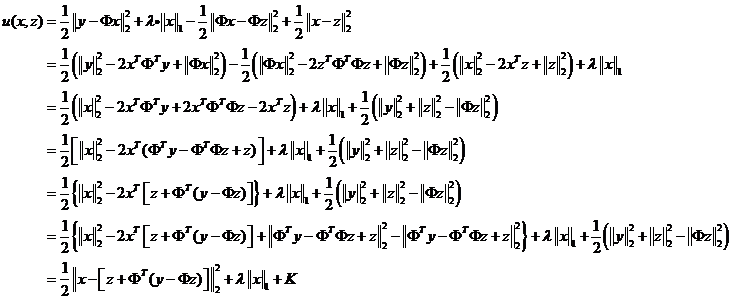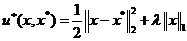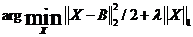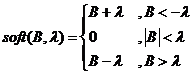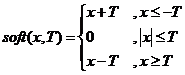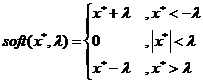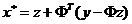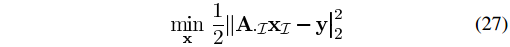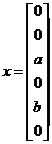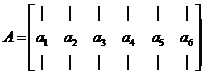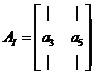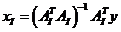彻底理解了迭代硬阈值IHT以后,很自然的会想到:如果将软阈值(SoftThresholding)函数与Majorization-Minimization优化框架相结合形成迭代软阈值(Iterative Soft Thresholding,IST)算法(另一种常见简称为ISTA,即IterativeSoftThresholding Algorithm,另外Iterative有时也作Iterated),应该可以解决如下优化问题[1]:
此即基追踪降噪(Basis Pursuit De-Noising, BPDN)问题。
1、迭代软阈值算法流程
为了解决优化问题(将原a换为习惯的x)
执行迭代算法
其中Ψλ是对每一个数值计算软阈值函数值
这个算法称为迭代软阈值(Iterative Soft Thresholding,IST)算法。
2、迭代软阈值算法推导
基追踪降噪(Basis Pursuit De-Noising, BPDN)问题的目标函数
由于目标函数f(x)并不容易优化,根据Majorization-Minimization优化框架,可以优化替代目标函数
这里要求||Φ||2<1,则有
下面,我们对替代目标函数进行变形化简
其中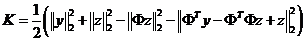
其中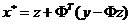
对!这正是软阈值(SoftThresholding)函数要解决的以下优化问题
对于标准的软阈值(Soft Thresholding)函数来说,这个优化问题的解是
注意:这里的B是一个向量,应该是逐个元素分别执行软阈值函数;其中标准的软阈值(SoftThresholding)函数是:
将符号换为此处的优化问题
则解为
注意:这里的x*是一个向量,应该是逐个元素分别执行软阈值函数;其中
然后我们根据Majorization-Minimization优化框架的流程进行迭代即可,注意z代表xn,即当前迭代值,而优化解soft(x*,λ)代表xn+1,用于下次迭代。
由于这个算法的整个过程相当于迭代执行软阈值(SoftThresholding)函数,所以把它称为迭代软阈值(Iterative Soft Thresholding)算法。
3、迭代软阈值算法MATLAB代码
在IST函数中,一共规定了三种IST跳出迭代的条件:第一个是重构结果经Phi变换后与原先y的差异,第二是最大迭代次数,第三个是重构结果x两次相邻迭代的差异。
以下为2016-08-12更新版本V1.1,相比于原先的V1.0改动之处为第1个跳出迭代循环的条件参考TwIST作了修改:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | function [ x ] = IST_Basic( y,Phi,lambda,epsilon,loopmax ) % Detailed explanation goes here %Version: 1.0 written by jbb0523 @2016-08-09 %Version: 1.1 modified by jbb0523 @2016-08-12 if nargin < 5 loopmax = 10000; end if nargin < 4 epsilon = 1e-2; end if nargin < 3 lambda = 0.1* max ( abs (Phi'*y)); end [y_rows,y_columns] = size (y); if y_rows<y_columns y = y'; %y should be a column vector end soft = @(x,T) sign (x).* max ( abs (x) - T,0); n = size (Phi,2); x = zeros (n,1); %Initialize x=0 f = 0.5*(y-Phi*x)'*(y-Phi*x)+lambda* sum ( abs (x)); %added in v1.1 loop = 0; fprintf ( '\n' ); while 1 x_pre = x; x = soft(x + Phi'*(y-Phi*x),lambda); %update x loop = loop + 1; f_pre = f; %added in v1.1 f = 0.5*(y-Phi*x)'*(y-Phi*x)+lambda* sum ( abs (x)); %added in v1.1 if abs (f-f_pre)/f_pre<epsilon %modified in v1.1 fprintf ( 'abs(f-f_pre)/f_pre<%f\n' ,epsilon); fprintf ( 'IST loop is %d\n' ,loop); break ; end if loop >= loopmax fprintf ( 'loop > %d\n' ,loopmax); break ; end if norm (x-x_pre)<epsilon fprintf ( 'norm(x-x_pre)<%f\n' ,epsilon); fprintf ( 'IST loop is %d\n' ,loop); break ; end end end |
原先的V1.0版本:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | function [ x ] = IST_Basic( y,Phi,lambda,epsilon,loopmax ) % Detailed explanation goes here %Version: 1.0 written by jbb0523 @2016-08-09 if nargin < 6 loopmax = 10000; end if nargin < 5 epsilon = 1e-6; end if nargin < 4 lambda = 0.1* max ( abs (Phi'*y)); end [y_rows,y_columns] = size (y); if y_rows<y_columns y = y'; %y should be a column vector end soft = @(x,T) sign (x).* max ( abs (x) - T,0); n = size (Phi,2); x = zeros (n,1); %Initialize x=0 loop = 0; fprintf ( '\n' ); while 1 x_pre = x; x = soft(x + Phi'*(y-Phi*x),lambda); %update x loop = loop + 1; if norm (y-Phi*x)<epsilon fprintf ( 'norm(y-Phi*x)<%f\n' ,epsilon); fprintf ( 'IST loop is %d\n' ,loop); break ; end if loop >= loopmax fprintf ( 'loop > %d\n' ,loopmax); break ; end if norm (x-x_pre)<epsilon fprintf ( 'norm(x-x_pre)<%f\n' ,epsilon); fprintf ( 'IST loop is %d\n' ,loop); break ; end end end |
该函数非常简单,核心程序就一行,其它均为配角,为这一行服务的:
| 1 | x = soft(x + Phi'*(y-Phi*x),lambda); %update x |
4、迭代软阈值算法测试
这里首先按传统的测试程序进行重构测试,这里的λ取值参考了文献【2】作者主页给出的代码里的方法(可以自己试一下,这个值到底是1还是2其实影响不大):
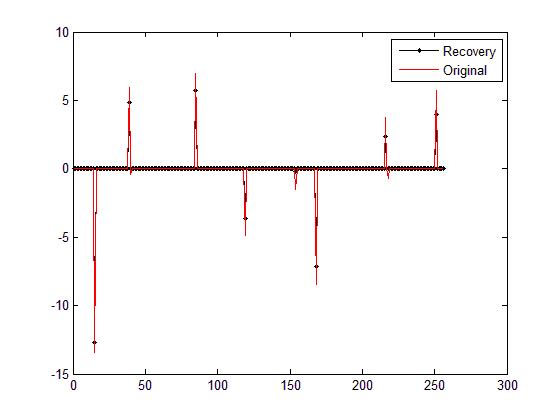
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | clear all ; close all ; clc ; M = 64; %观测值个数 N = 256; %信号x的长度 K = 10; %信号x的稀疏度 Index_K = randperm (N); x = zeros (N,1); x(Index_K(1:K)) = 5* randn (K,1); %x为K稀疏的,且位置是随机的 %x(Index_K(1:K)) = sign(5*randn(K,1)); Phi = randn (M,N); %测量矩阵为高斯矩阵 Phi = orth (Phi ')' ; sigma = 0.005; e = sigma* randn (M,1); y = Phi * x + e; %得到观测向量y % y = Phi * x;%得到观测向量y %% 恢复重构信号x tic % lamda = sigma*sqrt(2*log(N)); lamda = 0.1* max ( abs (Phi'*y)); fprintf ( '\nlamda = %f\n' ,lamda) %x_r = BPDN_quadprog(y,Phi,lamda); x_r = IST_Basic(y,Phi,lamda); toc %% 绘图 figure ; plot (x_r, 'k.-' ); %绘出x的恢复信号 hold on; plot (x, 'r' ); %绘出原信号x hold off; legend ( 'Recovery' , 'Original' ) fprintf ( '\n恢复残差:' ); fprintf ( '%f\n' , norm (x_r-x));%恢复残差 |
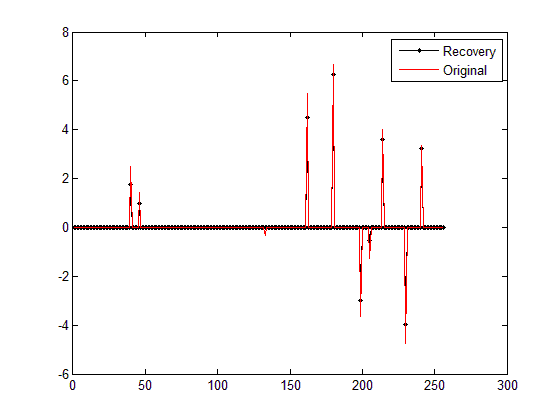
运行结果如下:(信号为随机生成,所以每次结果均不一样)
1)图
2)CommandWindows:
lamda= 0.177639
norm(x-x_pre)<0.000001
ISTloop is 106
Elapsedtime is 0.008842 seconds.
恢复残差:1.946232
从图中可以看出,重构结果的位置基本都是正确的,但确比原始信号都要小一些,为什么呢?从Command Windows的输出结果来看,IST迭代的106次,跳出迭代的条件是x在相邻两次迭代中基本不变了(norm(x-x_pre)<0.000001),也就是说最优点x已经基本不变了,若同样执行使用MATLAB自带的quadprog的基追踪降噪BPDN_quadprog函数(参见压缩感知重构算法之基追踪降噪),重构结果是正常的,到底为什么本文的IST重构结果得不到近似的x呢?难道理论推导有问题?
直到看了文献【2】中的Debiasing:
文中提到:“In many situations, itis worthwhile to debias the solution as a postprocessing step, to eliminate theattenuation of signal magnitude due to the presence of the regularization term.”,直译过来就是“在很多场合,作为一个后处理步骤对结果进行除偏(debias)是很值得的,用于消除由于正则项的存在对信号幅度造成的衰减”,读到这里就明白了,为什么本文的IST重构结果总是与真实的x幅度差一些呢?这是因为IST求解的优化问题含有正则项(regularizationterm),即λ||x||1。直观地来讲,因为目标函数中存在λ||x||1项,在最优化min时这个也要尽量的小,所以IST的恢复的结果比实际的x幅度要小一些(与参数λ有关)。解决这个问题的办法就是对结果进行除偏(debias,注:有道词典查不到此单词,也没看中文文献是如何翻译的,直接根据词根琢磨了一下自己瞎翻译的)。
如何除偏(debias)呢?接着来看:“Inthe debiasing step, we fix at zero those individual components or groups thatare zero at the end of the SpaRSA process, and minimize the objective over theremaining elements.”,翻译一下就是“将SpaRSA重构结果中的为零的项固定为零,然后在剩除项上对目标函数进行最小化”,简单一点说就是优化文中的式(27)(正好与本文IST解决的问题相同,后来会专门分析SpaRSA算法):
其中AI的含义更清晰的解释如下:
若SpaRSA重构的x为:
原来的矩阵A为:
则AI等于原矩阵A只保留第3列(对应x中的元素a)和第5列(对应x中的元素b)的子矩阵:
文献【2】后面继续谈到,若要求解式(27)可以使用共轭梯度法(Conjugate gradient)。实际上,式(27)的最优解为最小二乘解(熟悉匹配追踪系列算法的应该对这个很清楚,可参见压缩感知中的数学知识:投影矩阵(projectionmatrix)),即
在SpaRSA算法中,作者给出的官方代码里包括了debias过程,由一个参数来控制是否对重构结果执行debias过程,这里为了简单,就不修改IST函数了,直接在测试代码中加入debias代码:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 | clear all ; close all ; clc ; M = 64; %观测值个数 N = 256; %信号x的长度 K = 10; %信号x的稀疏度 Index_K = randperm (N); x = zeros (N,1); x(Index_K(1:K)) = 5* randn (K,1); %x为K稀疏的,且位置是随机的 %x(Index_K(1:K)) = sign(5*randn(K,1)); Phi = randn (M,N); %测量矩阵为高斯矩阵 Phi = orth (Phi ')' ; sigma = 0.005; e = sigma* randn (M,1); y = Phi * x + e; %得到观测向量y % y = Phi * x;%得到观测向量y %% 恢复重构信号x tic % lamda = sigma*sqrt(2*log(N)); lamda = 0.1* max ( abs (Phi'*y)); fprintf ( '\nlamda = %f\n' ,lamda) %x_r = BPDN_quadprog(y,Phi,lamda); x_r = IST_Basic(y,Phi,lamda); toc %Debias [xsorted inds] = sort ( abs (x_r), 'descend' ); AI = Phi(:,inds(xsorted(:)>1e-3)); xI = pinv (AI '*AI)*AI' *y; x_bias = zeros ( length (x),1); x_bias(inds(xsorted(:)>1e-3)) = xI; %% 绘图 figure ; plot (x_r, 'k.-' ); %绘出x的恢复信号 hold on; plot (x, 'r' ); %绘出原信号x hold off; legend ( 'Recovery' , 'Original' ) fprintf ( '\n恢复残差(original):' ); fprintf ( '%f\n' , norm (x_r-x));%恢复残差 %Debias figure ; plot (x_bias, 'k.-' ); %绘出x的恢复信号 hold on; plot (x, 'r' ); %绘出原信号x hold off; legend ( 'Recovery-debise' , 'Original' ) fprintf ( '恢复残差(debias):' ); fprintf ( '%f\n' , norm (x_bias-x));%恢复残差 |
运行结果如下:(信号为随机生成,所以每次结果均不一样)
1)图:
第一幅图(IST重构结果与原信号对比):
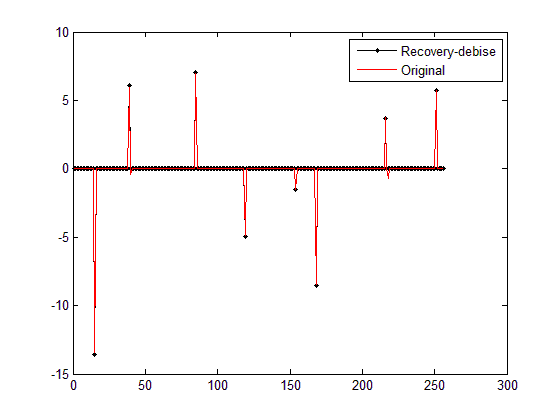
第二幅图(对IST重构结果debias后的结果与原信号对比):
2)CommandWindows:
lamda = 0.405767
norm(x-x_pre)<0.000001
IST loop is 74
Elapsed time is 0.007175 seconds.
恢复残差(original):3.736317
恢复残差(debias):0.847947
从第二幅图的结果来看,debias后的结果已与BPDN_quadprog函数结果(参见压缩感知重构算法之基追踪降噪)在同一个水平了。
值得注意的是,在求最小二乘解的公式里包含矩阵求逆的过程,矩阵求逆在大规模(large scale)问题中是一个比较麻烦的问题,IST等迭代算法(包括IHTs等)本身相比于MP等算法的优势即为不含矩阵求逆,计算效率高,因此实际中求解文献【2】的式(27)不应该直接采用如上包含矩阵求逆的方式,尤其是大规模问题,否则IST算法计算量小的优势就没有了,此处仅是为了示范debias的效果。
5、结束语
值得注意的是,一般文献中出现的IST或ISTA简称中的“S”并非指的是“soft”,而是“shrinkage”,即“IteratedShrinkage/ThresholdingAlgorithm”,至于“shrinkage”是什么意思呢?我们还是先来看一下有道词典吧:
那么Iterative Soft Thresholding和Iterated Shrinkage/Thresholding有什么区别呢?你要认为它们是一样的也没问题,因为从文献中来看,很多作者的确是这么认为的;另外,还可以认为Iterative Soft Thresholding是Iterated Shrinkage/Thresholding的一种特殊情况,即每次迭代时正好是求软阈值函数时的特殊情况,而Iterated Shrinkage/Thresholding更是一种广义的称呼。
值得注意的是,本文参考文献很少,且均是与IST“不相关”的,这是因为没有哪一种文献明确提出IST,所以也不知道引用哪个了。
在下一篇中,我们从多篇文献中来看一看究竟什么是“Shrinkage”……
IST:Iterative Shrinkage/Thresholding和Iterative Soft Thresholding
6、参考文献
【1】Chen S S, Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J]. SIAM review, 2001, 43(1): 129-159.
【2】WrightS J, Nowak R D, Figueiredo M A T. Sparse reconstruction by separable approximation.[J]. IEEE Transactions on Signal Processing, 2009,57(7):3373-3376.