本文主要是介绍最优化技术——第七周周四 线性规划与单纯线性法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 单纯形法的思路
- 例题:
- 单纯形法的迭代原理
- 1、选择初始基,确定初始基本可行解
- 2、 判断当前解是否是最优解
- 3、 解的改进
- - 解的改进面临三个问题:
- 单纯形表——工具
- 4、检验当前基本可行解是否为最优解?
- - 最优解判别定理
- 例: 用单纯形法求下列线性规划的最优解
- 1)将问题化为标准型,加入松弛变量 X 3 X_3 X3 、 X 4 X_4 X4
- 2) 求出线性规划的初始基可行解,列出初始单纯形表。
- 3)进行最优性检验
- 4) 从一个基可行解转换到另一个目标值更大的基可行解,列出新的单纯形表
- 系数矩阵中没有现成的单位阵,怎么办?
- 人工变量法(**大M法**和两阶段法)
- 两阶段法
- 总结:
- 无界解示例:
- 本章内容小结:
- 课后作业:
单纯形法的思路
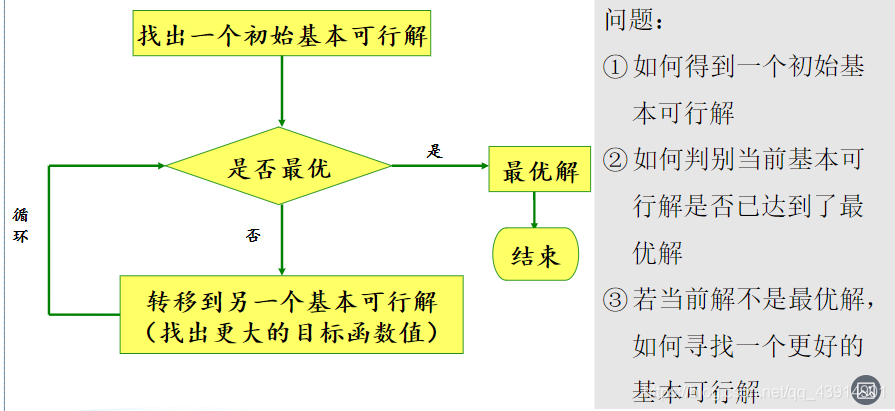
例题:
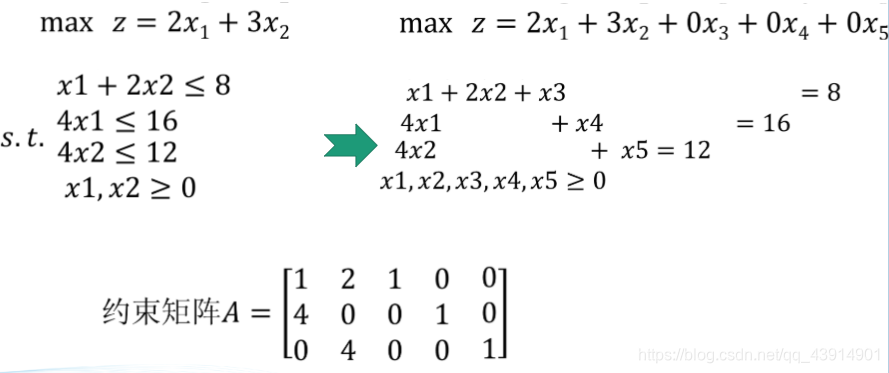
单纯形法的迭代原理
1、选择初始基,确定初始基本可行解

2、 判断当前解是否是最优解

3、 解的改进

- 解的改进面临三个问题:




单纯形表——工具

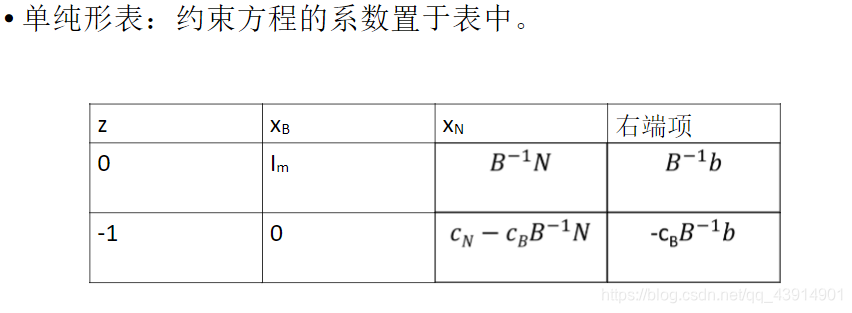
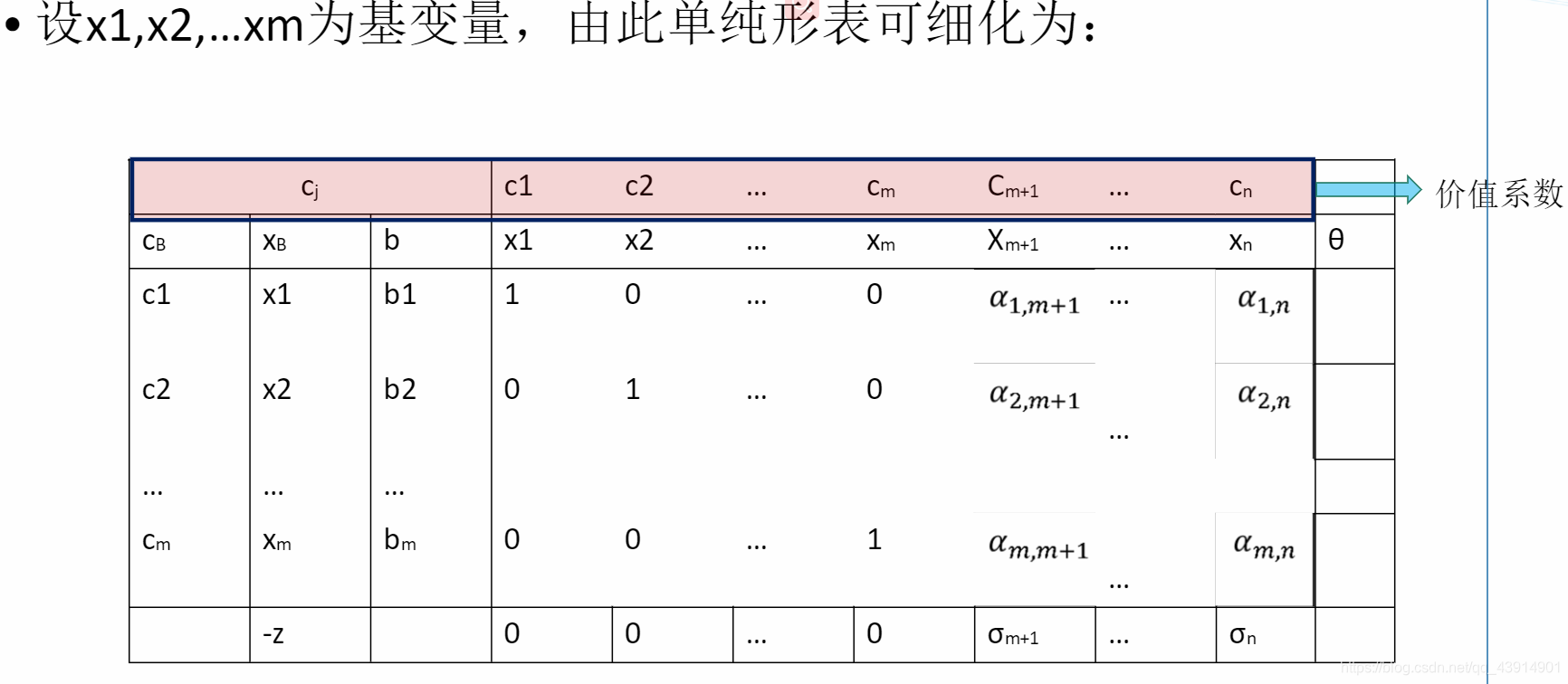




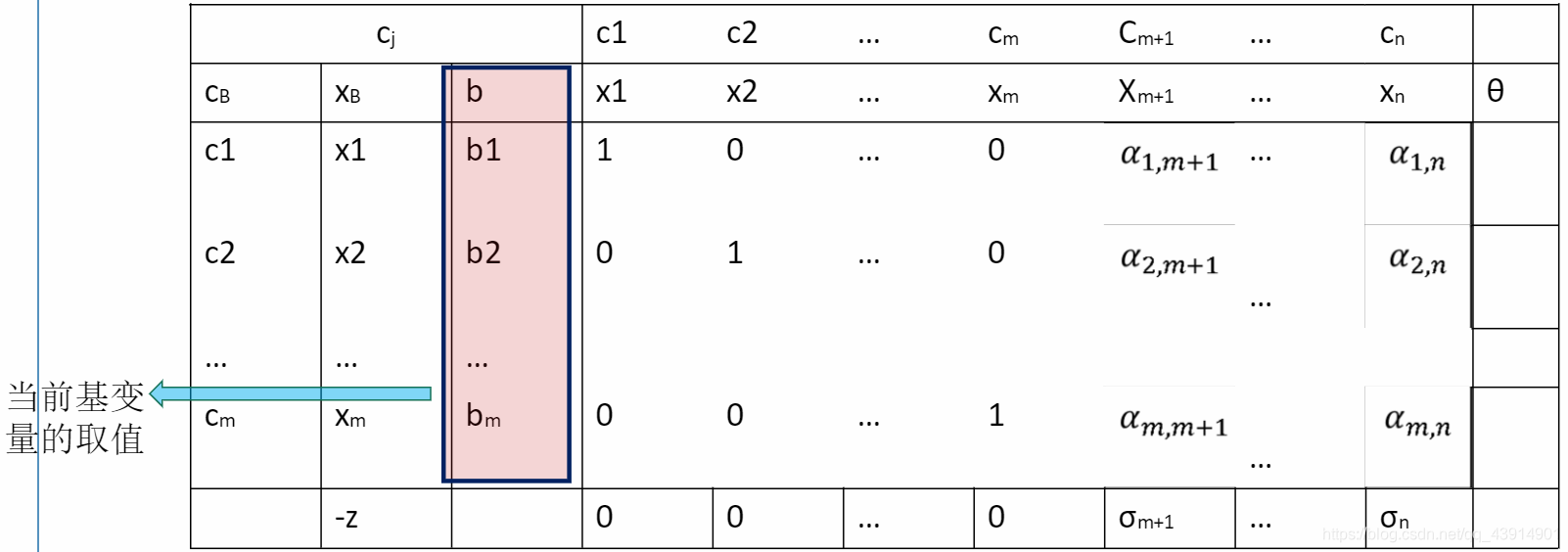

4、检验当前基本可行解是否为最优解?
- 最优解判别定理
对于求最大目标函数的问题中,对于某个基本可行解,如果所有检验数 δ j \delta_j δj < \lt < 0,
则这个基可行解是最优解。(即非基变量的检验数均小于0,存在唯一最优解)非基变量的检验数存在等于0,无穷多最优解
存在某非基变量xj的检验数 大于0,但该变量所对应的所有系数 a i j aij aij 均小于等于0,无界解。
例: 用单纯形法求下列线性规划的最优解
1)将问题化为标准型,加入松弛变量 X 3 X_3 X3 、 X 4 X_4 X4

2) 求出线性规划的初始基可行解,列出初始单纯形表。

3)进行最优性检验
如果表中所有检验数 δ j \delta_j δj ≤ \le ≤ 0,则表中的基可行解就是问题的最优解,计算停止。否则继续下一步
4) 从一个基可行解转换到另一个目标值更大的基可行解,列出新的单纯形表


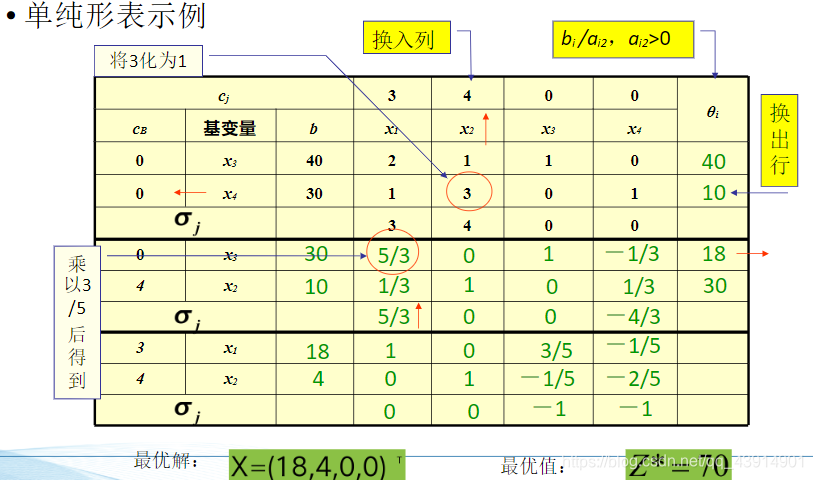
系数矩阵中没有现成的单位阵,怎么办?
加入人工变量
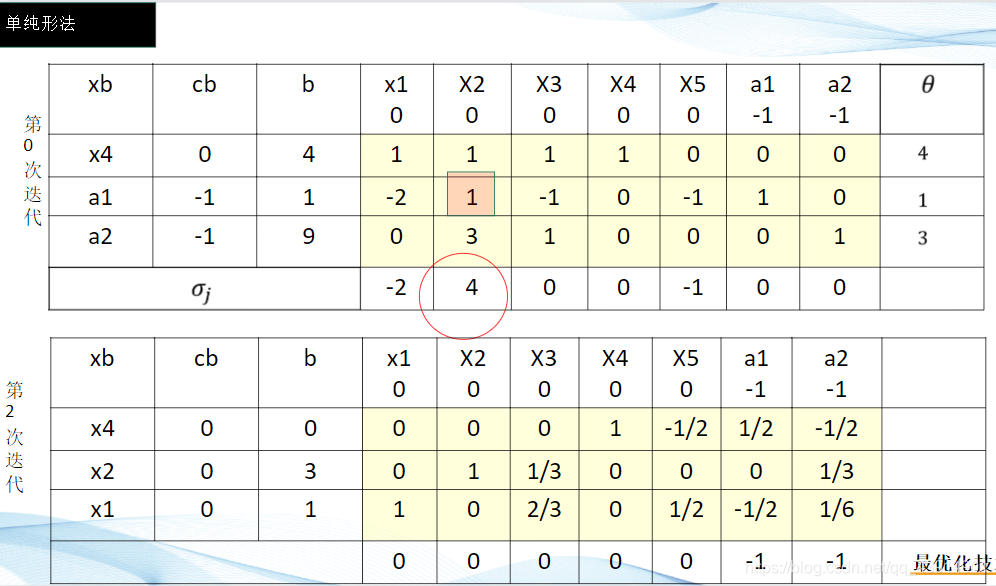
人工变量法(大M法和两阶段法)
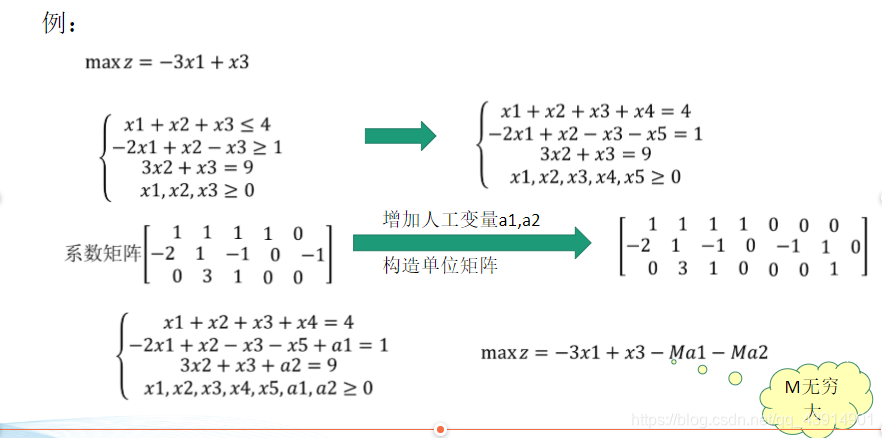
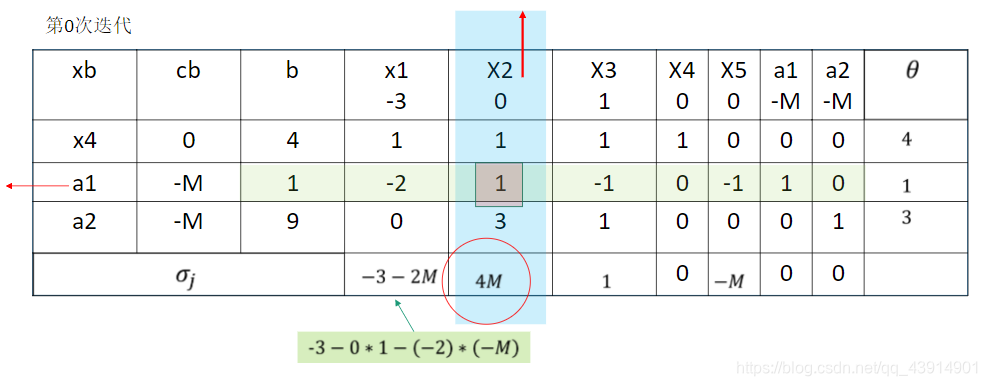
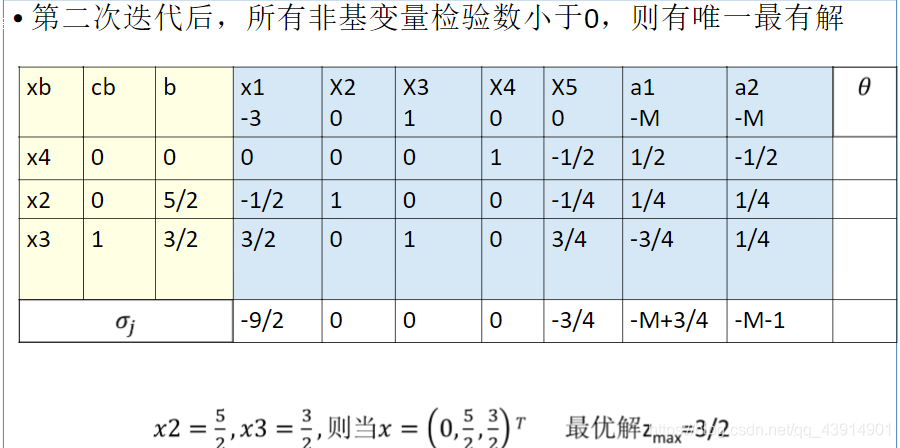
两阶段法

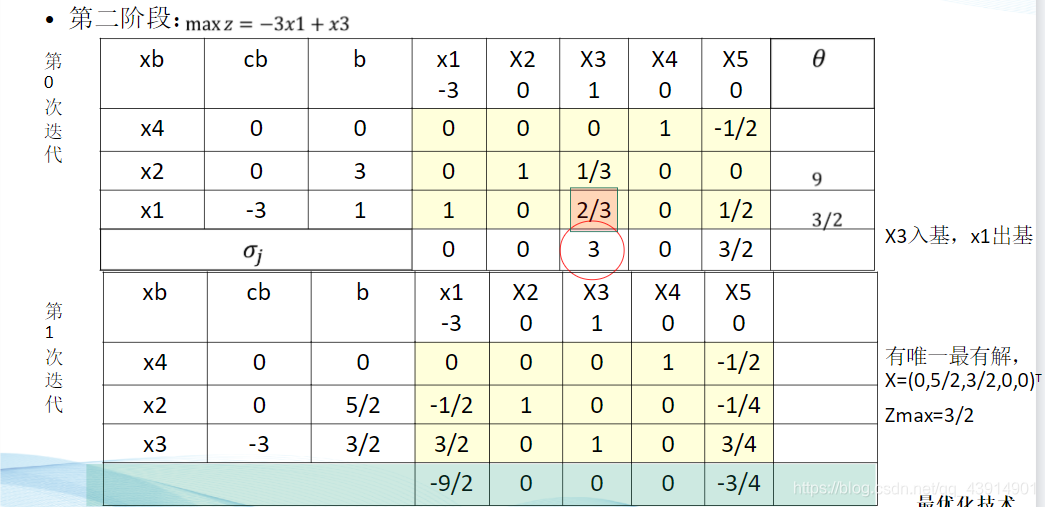
总结:
1)当所有非基变量的检验数都小于零,则原问题有唯一最优解;
2)当所有非基变量的检验数都小于等于零,注意有等于零的检验数,则有无穷多个最优解;
3)当任意一个大于零的非基变量的检验数,其对应的ajk(求最小比值的分母,即该检验数所对应的该列的数)都小于等于零时,则原问题有无界解;
4)添加人工变量后,当所有非基变量的检验数都小于等于零,而基变量中有人工变量时,则原问题无可行解。
无界解示例:
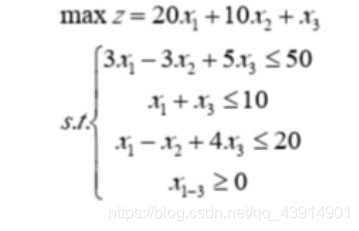
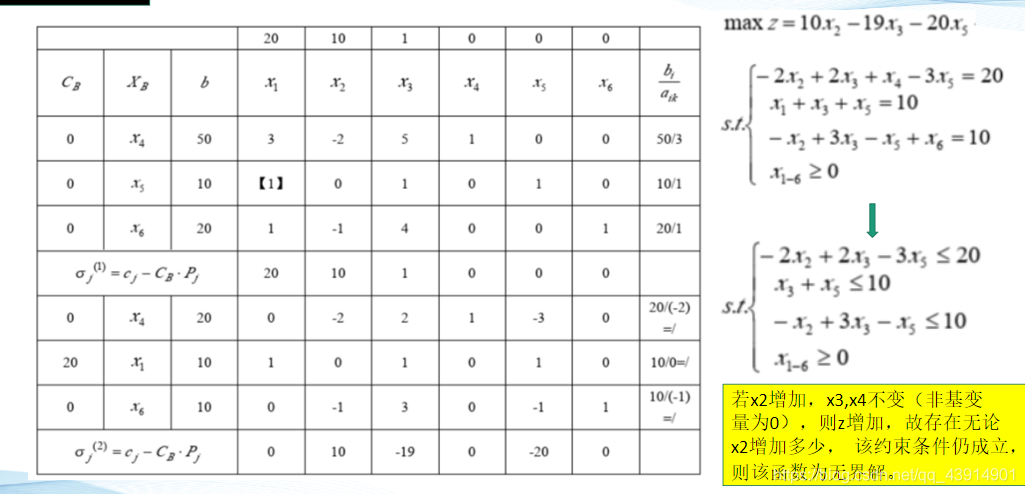
本章内容小结:

课后作业:

这篇关于最优化技术——第七周周四 线性规划与单纯线性法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




