牛客——丢手绢（尺取法）

本文主要是介绍牛客——丢手绢（尺取法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网
 

题目描述

“丢~丢~丢手绢，轻轻地放在小朋友的后面，大家不要告诉她，快点快点抓住她，快点快点抓住她。”

牛客幼儿园的小朋友们围成了一个圆圈准备玩丢手绢的游戏，但是小朋友们太小了，不能围成一个均匀的圆圈，即每个小朋友的间隔可能会不一致。为了大家能够愉快的玩耍，我们需要知道离得最远的两个小朋友离得有多远（如果太远的话牛老师就要来帮忙调整队形啦！）。

因为是玩丢手绢，所以小朋友只能沿着圆圈外围跑，所以我们定义两个小朋友的距离为沿着圆圈顺时针走或者逆时针走的最近距离。

输入描述:

第一行一个整数N，表示有N个小朋友玩丢手绢的游戏。
接下来的第2到第n行，第i行有一个整数，表示第i-1个小朋友顺时针到第i个小朋友的距离。
最后一行是第N个小朋友顺时针到第一个小朋友的距离。

输出描述:

输出一个整数，为离得最远的两个小朋友的距离。

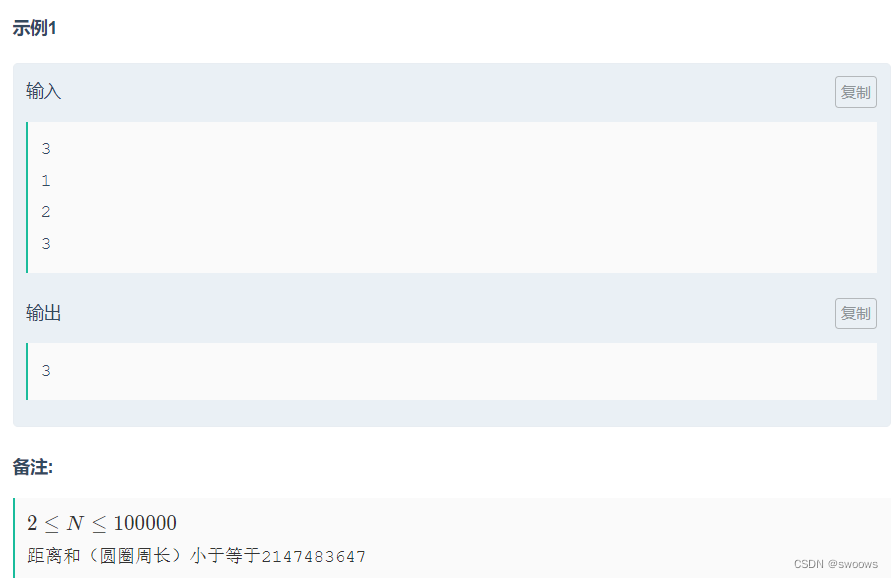
       尺取法是一种双指针算法，通常用于解决一些区间问题。它的基本思想是维护一个区间，然后通过移动左右指针来调整区间的大小和位置，以便找到符合条件的解。在这个问题中，我们需要找到离得最远的两个小朋友之间的距离。我们可以使用尺取法来解决这个问题。具体来说，我们可以使用两个指针i和j来表示当前考虑的两个小朋友之间的距离。我们可以让指针i从0开始遍历数组，并让指针j从i开始向右移动，直到找到一个位置k，使得从i到k和从k到i+n（n是数组长度）之间的距离最大。然后，我们可以更新答案，并将指针i向右移动一位。重复这个过程直到遍历完整个数组。

       这道题的思路很明显用双指针来做。(核心是判断指针r是否需要复位来判断是否是尺取法)。

      细节 cnt+=a[(j++)%n];

        这行代码是尺取法的核心部分。它使用了双指针技巧来找到两个子数组，使它们的元素和最接近数组元素和的一半。具体来说，它使用了一个循环来不断增加cnt的值，直到cnt大于等于数组元素和的一半。然后，它使用while循环来不断减少cnt的值，直到cnt小于数组元素和的一半。在这个过程中，j指针会不断向右移动，并使用模运算来保证它不会超出数组范围。当cnt大于等于数组元素和的一半时，我们就可以计算出当前两个子数组元素和之间的差值，并将其与之前计算出的差值进行比较，从而找到最小值。

#include<bits/stdc++.h>
using namespace std;
int main()
{int n;cin>>n;int a[100005];int sum=0;for(int i=0;i<n;i++){cin>>a[i];sum=sum+a[i];}int x=sum/2;int cnt=0;int res=0;int j=0;for(int i=0;i<n;i++){while(cnt<x){cnt=cnt+a[(j++)%n];}res=max(res,min(cnt,sum-cnt));cnt=cnt-a[i];}cout<<res;return 0;
}

这篇关于牛客——丢手绢（尺取法）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---