【早期疾病诊断 + 个性化医疗】通过 fundus 图，预测视网膜年龄

本文主要是介绍【早期疾病诊断 + 个性化医疗】通过 fundus 图，预测视网膜年龄，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

通过 fundus 图，预测视网膜年龄

• • 问题：预测年龄，解法：基于时间序列图像的渐进式标签分布学习 PLDL
  • • 子问题、算法拆解
    • 实验细节
    • 效果

 

---

问题：预测年龄，解法：基于时间序列图像的渐进式标签分布学习 PLDL

论文：https://link.springer.com/chapter/10.1007/978-3-031-43990-2_59

 
虽然理论上视网膜年龄和一个人的实际年龄（或称为慢性年龄）应该是一致的，但由于遗传因素、生活方式、环境影响和可能的疾病，视网膜的健康状态可能比实际年龄显得更老或更年轻。

换句话说，某些人的视网膜可能因为良好的保养而看起来比实际年龄年轻，而其他人可能因为健康问题而看起来比实际年龄老。

在医学和健康研究中，视网膜年龄被用作衡量个体衰老速度和健康状况的一个指标。

如果视网膜看起来比实际年龄老，这可能表示个体有更高的患病风险或已有未被发现的健康问题。

因此，准确地预测视网膜年龄对于早期诊断和治疗慢性疾病非常有价值。

 

作者提出的解决方案是使用一种基于时间序列图像的渐进式标签分布学习（Progressive Label Distribution Learning, LDL）方法。

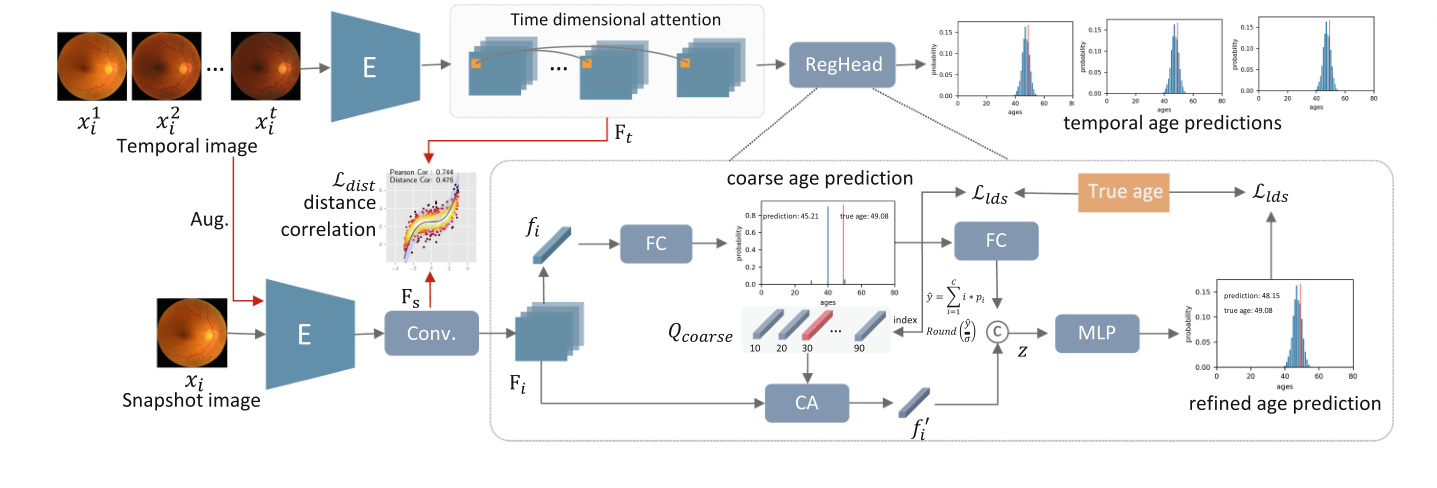
1. 时间序列图像的处理流程：

   • 输入一系列时间序列图像 $x_i^t$ 到一个编码器 ( E )，以提取特征 $F_t$。
   • 使用时间维度注意力模块（Time dimensional attention）来关注序列中不同时间点的关键特征。
   • 这些特征被传递到一个回归头（RegHead），用于做出时间序列的年龄预测，并以图表形式显示。

2. 快照图像的处理流程：

   • 输入一个快照图像 $x_i$ 到同样的编码器 ( E )，以提取特征 $F_s$。
   • 这些特征通过一个卷积层（Conv.）转换，然后与一个全连接层（FC）相结合，以生成对应于粗略年龄预测的特征 $f_i$。
   • 使用类别注意力机制（CA），这个机制结合了粗略年龄查询 $Q_{coarse}$ 和空间特征 $F_i$，以生成细致级别的特征 $f_i^{\prime }$。
   • 这些细致级别的特征与粗略年龄预测相结合，通过多层感知器（MLP）进行处理，以生成最终的精炼年龄预测。

3. 损失函数：

   • 使用距离相关性损失 $L_{dist}$，该损失基于时间序列特征 $F_t$ 和快照特征 $F_s$ 之间的关系。
   • 使用标签分布学习损失 $L_{lds}$，该损失考虑了真实年龄与预测年龄之间的差异。

4. 预测结果的可视化：

   • 年龄分布的条形图展示了对于给定图像样本的粗略和精炼年龄预测。
   • 每个预测都有一个对应的概率分布，显示了模型认为的最可能的年龄范围。

 

这种方法通过几个具体的子问题和相应的解法：

1. 子问题：数据源多样性和数据不一致性
   • 子解法：引入序数约束

为了处理不同数据源的图像特征对齐问题，这里引入序数约束。

这个步骤有助于确保来自不同群体的图像在特征空间中保持一致性和顺序性，从而提高模型在多个群体上的泛化能力。

 

假设我们有来自欧洲和亚洲的两组人群的视网膜图像，由于种族和环境因素，这两组图像在特征上可能有所不同。

为了确保我们的模型能够正确理解和处理这些差异，我们引入了序数约束。

这意味着，如果亚洲队列中一个40岁的个体的视网膜特征应该与欧洲队列中一个40岁个体的特征相似，序数约束会促使模型学习这种年龄相关的相似性，即使他们来自不同的数据源。

 

2. 子问题：标签的不确定性和个体差异
   • 子解法：两阶段LDL回归头

为了应对年龄标签的不确定性和个体间的差异，研究中设计了一个两阶段的 PLDL 回归头。

它可以为每个图像估计一个适应性的年龄分布，这种方法允许模型更好地捕捉到个体间的差异和年龄标签的不确定性。

 

在估计年龄时，有些个体的视网膜图像可能由于遗传或生活方式的原因而看起来比实际年龄要老或年轻。

使用两阶段LDL回归头，模型首先为每个图像给出一个粗略的年龄分布（如40到50岁之间）。

在第二阶段，模型会细化这个预测，可能会调整分布更靠近45岁，这样更准确地反映了个体的视网膜图像与年龄的真实关系。

先粗调，再精调，这样就比直接精调快。
 

3. 子问题：利用时间序列图像的信息
   • 子解法：添加时间分支

为了利用视网膜图像随时间的演变信息，研究中添加了一个时间分支来建模序列视网膜图像。

这个时间分支可以捕捉到随时间的演变，并将这些信息作为辅助知识来增强模型对快照图像的预测性能。

这些子问题和解决方案在整体解决方案中的目的是确保从视网膜基金图像中估算出的视网膜年龄既准确又具有较强的泛化能力。

引入序数约束解决了来自不同数据源的不一致性，两阶段LDL回归头处理了标签不确定性和个体差异，而时间分支则利用了随时间变化的数据来提高预测精度。

 

假设一个患者在过去10年中每年都进行了视网膜检查，我们有一系列随时间变化的视网膜图像。

通过添加时间分支，模型不仅可以看到每一张独立的图像，还可以捕捉到随时间的变化，如视网膜可能出现的微小变化或衰老迹象。

这样，模型在对单个图像进行年龄估计时，可以利用这种时间序列知识来增强预测的准确性。

例如，如果某个年龄段的变化在时间序列中很常见，模型将学会在见到类似的变化时调整单张图像的年龄估计。

 

---

子问题、算法拆解

怎么估算视网膜年龄，涉及多个子问题和对应解法：

1. 子问题：粗略和细致的年龄估算
   • 子解法：两阶段标签分布学习（Progressive Label Distribution Learning）

这种方法首先使用全局特征预测粗略的年龄分布，然后通过类别注意力机制生成细致的特征来提炼年龄预测。

这样做的原因是考虑到年龄标签本身的不确定性和人群间的个体差异。

两阶段处理提供了从粗略到细致的逐步精确化，有助于更准确地捕捉个体的年龄特征。

 

比如估算一个45岁的个体的视网膜图像，第一阶段的粗略预测可能给出一个分布，显示这个人的视网膜年龄在40到50岁之间。

然后，第二阶段的细致预测会分析更具体的视网膜特征，如血管状况或色素沉着，进一步细化预测，可能将年龄范围缩小到44到46岁之间，更接近真实年龄。
 

2. 子问题：年龄关系的顺序信息丢失和不同数据源的特征不一致性
   • 子解法：跨域序数特征对齐（Cross-Domain Ordinal Feature Alignment）

为了解决传统分类任务中丢失的年龄顺序信息和来自不同数据源的特征不一致性，引入了序数约束和特征对齐。

通过构造特征三元组并强制特征距离与相对年龄差一致，以及最小化相同类别内的特征距离，可以更好地保持年龄的顺序性和不同数据源之间的特征一致性。

 

比如在一个多国多中心的研究中，从不同国家的队列中收集了视网膜图像。

一个来自意大利的50岁的患者和一个来自中国的50岁的患者可能由于种族和环境因素，在视网膜图像上表现出不同的特征。

使用序数特征对齐，模型将学会识别和调整这些特征，以确保年龄估计不受数据源差异的影响。
 

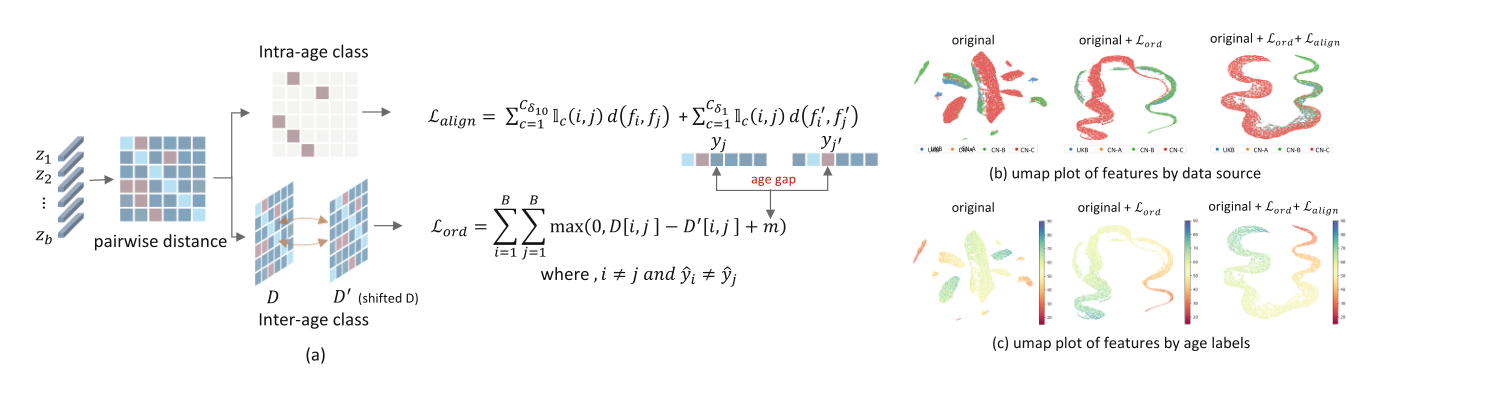
上图，对如何改善特征空间中年龄估计的序数信息和跨不同数据集特征一致性的洞察，以及这些技术的影响如何在特征可视化中体现出来：

1. 左图的解释：

   • 领域感知序数特征对齐的约束：
     • 显示了如何计算序数特征对齐（$L_{ord}$）和类内特征对齐（$L_{align}$）的损失函数。这些函数有助于学习在特征空间中保持年龄类别的顺序关系。
     • 序数特征对齐损失函数 $L_{ord}$ 通过比较特征对 $z_i$ 和 $z_j$ 之间的距离矩阵 ( D ) 和偏移后的距离矩阵 $D^{\prime }$，以确保特征的距离反映实际的年龄差距。
     • 这通过一个最大化函数完成，其中包括一个间隔 ( m )，以确保正确的序数关系被学习。
     • 类内特征对齐损失 $L_{align}$ 旨在通过最小化相同年龄类别内样本的特征距离，使来自同一年龄类别的特征更加接近。

2. 右图的解释：

   • 特征可视化结果：
     • (b)部分展示了数据源（如UKB、CN-A、CN-B、CN-C）的UMAP特征映射图。这个映射图在没有序数特征对齐和类内特征对齐约束的情况下（original），以及在应用了序数特征对齐约束 $L_{ord}$ 和 $L_{ord}+L_{align}$ 之后的对比。
     • ©部分展示了按年龄标签的UMAP特征映射图。同样地，这个映射图显示了在没有特征对齐约束的情况下（original）和在应用了 $L_{ord}$ 和 $L_{ord}+L_{align}$ 之后的对比。
     • 这些可视化结果表明，通过应用序数和类内特征对齐，特征空间中相似和相关的样本更加紧密和有序地聚集在一起，反映了它们在数据源和年龄上的相似性。

 

3. 子问题：有限的时间序列数据与大规模快照数据的集成学习
   • 子解法：时间序列图像的联合学习（Co-Learning with Temporal Fundus Images）

考虑到时间序列数据可能受限，而快照数据较为丰富，采用了时间序列图像与快照图像的联合学习方法。

这样做的目的是利用时间序列数据中包含的额外衰老信息来增强快照图像上模型的表现。

时间维度的注意力模块帮助捕捉时间序列图像间的相关性，而距离相关性损失确保快照特征与时间序列特征保持相似的关系。

 
比如一个研究项目中有一小部分参与者每年都进行视网膜检查，累积了10年的数据，而另一大部分参与者只有一次检查的数据。

在这种情况下，模型将使用有限的时间序列数据来学习年龄如何影响视网膜的变化，然后将这种知识应用于那些只有单次快照数据的大规模参与者群体，以提高年龄估计的准确性。

例如，如果时间序列显示随着年龄增长，某种特定的视网膜特征变得更为明显，那么即使是在缺乏时间序列的个体中，模型也会学习到这一点，并在单次快照中寻找这些特征的迹象。

 

基于时间序列图像的渐进式标签分布学习 =

• 粗略和细致的年龄估算（两阶段标签分布学习） +
• 年龄关系的顺序信息丢失和不同数据源的特征不一致性（跨域序数特征对齐） +
• 有限的时间序列数据与大规模快照数据的集成学习（时间序列图像的联合学习）

两阶段标签分布学习处理了年龄估算的不确定性和个体差异。

跨域序数特征对齐处理了不同数据源间的特征一致性和年龄关系的顺序信息保持。

时间序列图像的联合学习利用了有限的时间序列数据来增强模型在更广泛的快照数据集上的表现。

 

---

实验细节

1. 子问题：如何处理多个不同数据集的集成
   • 子解法：使用多源数据集

研究中整合了多个不同来源的数据集（如UK Biobank、CN-A、CN-B、CN-C），以增加数据的多样性和丰富性。

这种方法可以帮助模型更好地泛化到不同人群和环境中，因为不同数据集可能代表不同的人群特征。

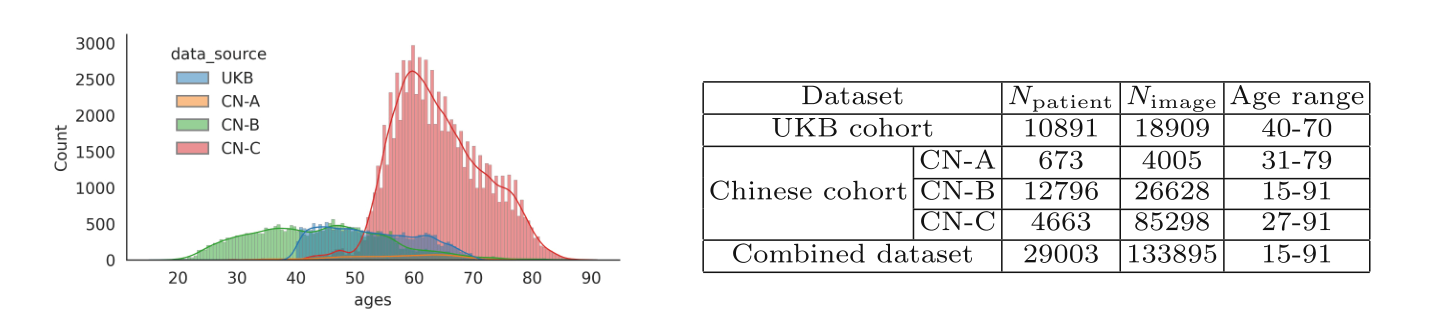
上图是视网膜数据集的概况，包括年龄分布和不同队列的患者和图像数量：

1. 左图 (a) 年龄分布：

   • 这是一个直方图，显示了四个不同队列（UKB, CN-A, CN-B, CN-C）的年龄分布。
   • 每个队列的年龄分布用不同的颜色表示，可见UKB队列主要集中在40至70岁，而CN-A、CN-B和CN-C队列的年龄分布更广泛。

2. 右图 (b) 人口统计数据：

   • 这是一个表格，总结了UKB队列和中国队列的人口统计信息。
   • 表格列出了每个队列的患者数量 $N_{patient}$，图像数量 $N_{image}$，以及年龄范围。
   • UKB队列有10891名患者和18909张图像，年龄范围是40-70岁。
   • CN-A队列有673名患者和4005张图像，年龄范围是31-79岁。
   • CN-B队列有12796名患者和26628张图像，年龄范围是15-91岁。
   • CN-C队列有4663名患者和85298张图像，年龄范围是27-91岁。
   • 合并的数据集包括29003名患者和133895张图像，年龄范围是15-91岁。

 

2. 子问题：如何确保模型在训练过程中的有效性和稳健性
   • 子解法：详细的训练细节设置

通过精心设计训练过程（如数据增强、图像大小调整、使用ResNet-50作为图像编码器、ADAM优化器、批大小、学习率和早停等），确保模型能够有效学习并在不同的数据集上达到较高的准确性。

 

效果

3. 子问题：如何衡量模型的性能
   • 子解法：使用标准评估指标

选用均绝对误差（MAE）和皮尔逊相关系数作为性能评估指标，这些指标可以客观地评估模型在年龄估计任务上的准确性和可靠性。

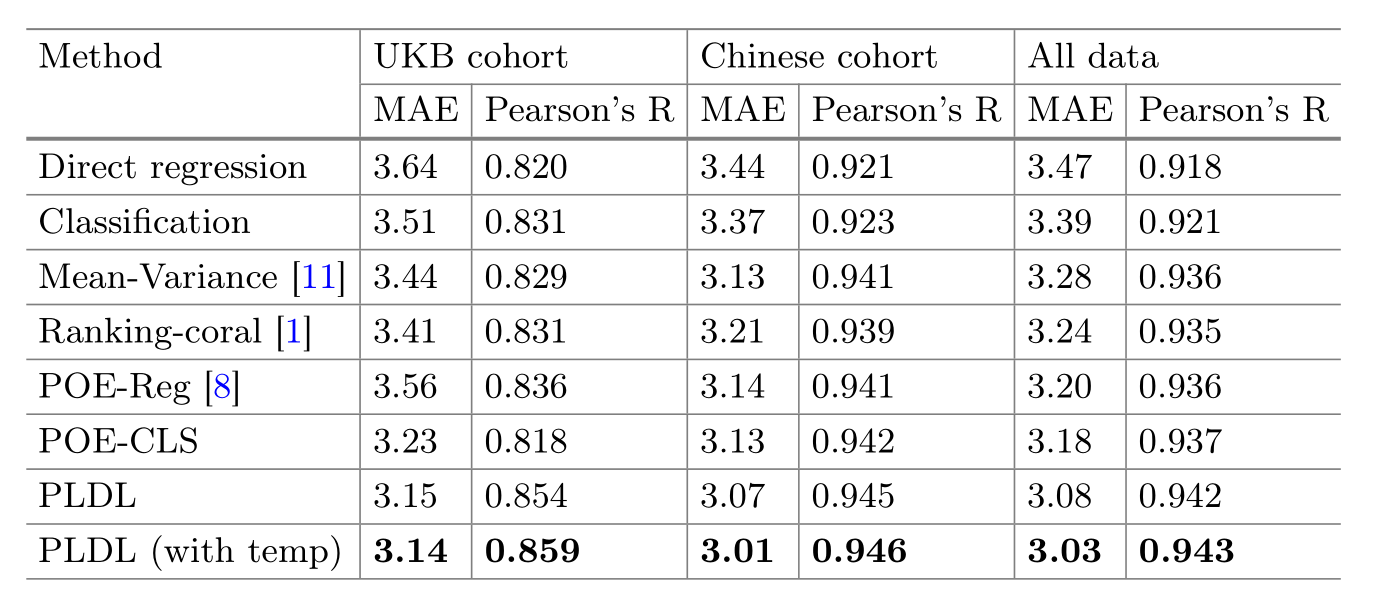
这张表格提出的方法与现有研究方法在两个不同队列（UKB队列和中国队列）以及所有数据上的比较结果。

比较的基准是平均绝对误差（MAE）和皮尔逊相关系数（Pearson’s R），这两个指标通常用来评估回归模型的性能。

各种方法的性能比较如下：

1. 直接回归（Direct regression）

   • 在UKB队列中MAE为3.64，皮尔逊相关系数为0.820；
   • 在中国队列中MAE为3.44，皮尔逊相关系数为0.921；
   • 在所有数据上MAE为3.47，皮尔逊相关系数为0.918。

2. 分类（Classification）

   • 在UKB队列中MAE为3.51，皮尔逊相关系数为0.831；
   • 在中国队列中MAE为3.37，皮尔逊相关系数为0.923；
   • 在所有数据上MAE为3.39，皮尔逊相关系数为0.921。

3. 均值-方差（Mean-Variance）

   • 在UKB队列中MAE为3.44，皮尔逊相关系数为0.829；
   • 在中国队列中MAE为3.13，皮尔逊相关系数为0.941；
   • 在所有数据上MAE为3.28，皮尔逊相关系数为0.936。

4. 排名-珊瑚（Ranking-coral）

   • 在UKB队列中MAE为3.41，皮尔逊相关系数为0.831；
   • 在中国队列中MAE为3.21，皮尔逊相关系数为0.939；
   • 在所有数据上MAE为3.24，皮尔逊相关系数为0.935。

5. POE-Reg

   • 在UKB队列中MAE为3.56，皮尔逊相关系数为0.836；
   • 在中国队列中MAE为3.14，皮尔逊相关系数为0.941；
   • 在所有数据上MAE为3.20，皮尔逊相关系数为0.936。

6. POE-CLS

   • 在UKB队列中MAE为3.23，皮尔逊相关系数为0.818；
   • 在中国队列中MAE为3.13，皮尔逊相关系数为0.942；
   • 在所有数据上MAE为3.18，皮尔逊相关系数为0.937。

7. PLDL（提出的方法）

   • 在UKB队列中MAE为3.15，皮尔逊相关系数为0.854；
   • 在中国队列中MAE为3.07，皮尔逊相关系数为0.945；
   • 在所有数据上MAE为3.08，皮尔逊相关系数为0.942。

8. PLDL（使用时间数据的提出的方法）

   • 在UKB队列中MAE为3.14，皮尔逊相关系数为0.859；
   • 在中国队列中MAE为3.01，皮尔逊相关系数为0.946；
   • 在所有数据上MAE为3.03，皮尔逊相关系数为0.943。

PLDL 方法（特别是结合时间序列数据的版本）在MAE和皮尔逊相关系数上通常优于其他比较方法，这表明PLDL在预测视网膜年龄方面的性能更好。

 

上图是，不同队列上的错误分布和平均绝对误差（MAE）结果。

1. 左图 (a) 年龄上的错误分布：

   • 顶部的直方图显示了UKB队列上的测试MAE，按年龄标签分布。MAE的平均值为3.14。
   • 底部的直方图显示了中国队列上的测试MAE，同样按年龄标签分布。MAE的平均值为3.01。
   • 这些直方图显示了在不同年龄段的预测误差分布，可以看出某些年龄段的预测误差较大。

2. 中图 (b) 中国队列的MAE：

   • 这是一个散点图，横轴是实际年龄（Chronological age），纵轴是通过模型预测的视网膜生物学年龄（Retinal biological age）。
   • 图表旁边的直方图显示了预测年龄与实际年龄差的分布。
   • 表格显示了MAE为3.016，皮尔逊相关系数为0.946，表明预测年龄与实际年龄之间有很高的一致性。

3. 右图 © UKB队列的MAE：

   • 类似中图，这也是一个散点图，显示了UKB队列上的预测年龄与实际年龄的关系。
   • 直方图显示预测年龄的分布。
   • 表格显示了MAE为3.148，皮尔逊相关系数为0.860，这也反映出预测年龄与实际年龄之间的高度相关性，尽管略低于中国队列。

虽然存在一些预测误差，但模型在预测视网膜生物学年龄方面整体上是准确且可靠的。

 

上图是几个样本的估计年龄分布案例。

对于每个样本，模型的粗略预测和精细预测的结果，以及基线分类模型的结果：

1. 样本 a 和 c 的解释：

   • 对于每个样本，左边的图像展示了视网膜基金摄影图。
   • 中间的两个分布图展示了从模型中得到的粗略预测和精细预测的年龄分布。
   • 蓝色条形图显示了各个年龄的概率分布，红色垂直线表示真实年龄。
   • 粗略预测提供了一个较宽的年龄分布，而精细预测则显示了一个更为集中的分布，更接近真实年龄。

2. 样本 b 和 d 的解释：

   • 与样本 a 和 c 类似，每个样本的右边图展示了基线分类模型的年龄分布预测。
   • 与粗略和精细预测相比，基线模型的预测可能不够精细，分布更宽泛。

3. 预测结果的比较：

   • 每组的最右边的图显示了基线分类模型的结果，它与模型的粗略和精细预测结果相比较，以评估模型性能的改进。

模型的精细预测结果，通常更紧密地集中在真实年龄附近，具有较高的预测精度。

这篇关于【早期疾病诊断 + 个性化医疗】通过 fundus 图，预测视网膜年龄的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---