本文主要是介绍Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 5——神经网络(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考)
课程网址:https://www.coursera.org/learn/machine-learning
参考资料:http://blog.csdn.net/SCUT_Arucee/article/details/50176159
一、神经网络的代价函数
1.1 神经网络的模型参数
假设我们有下图这样的神经网络:
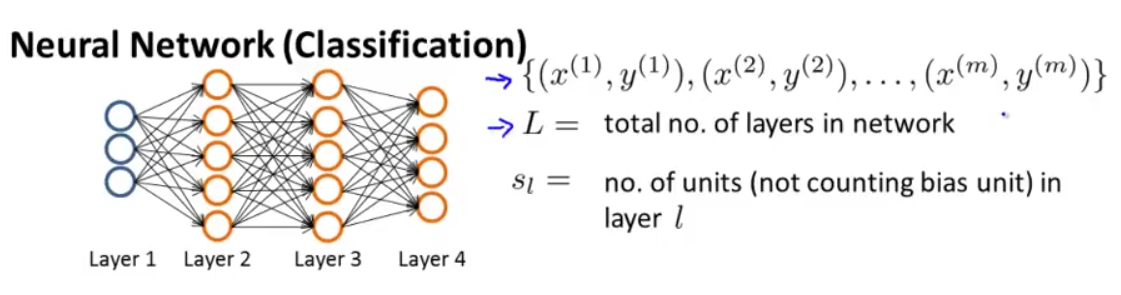
我们定义以下符号:
m 组训练数据
L→ 神经网络总的层数;
sl→ 第 l 层的单元数 (不包括偏差单元);
K→ 输出层的单元数。
① 对于两类分类问题:
y=0or1 ,只有一个输出单元, hΘ(x)∈R ,故 SL=1 ,即 K=1 。
② 对于多类分类问题:
y 是一个向量,y∈Rk , hΘ(x)∈Rk , SL=K(K≥3) 。
1.2 神经网络的代价函数
我们先来回忆一下逻辑回归代价函数的一般形式:
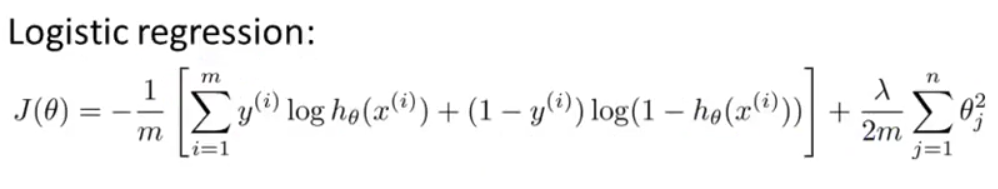
在此基础上,我们可以得到神经网络的代价函数。对于神经网络来说,输出不再是只有一个逻辑回归输出单元,取而代之的是有 K 个。
定义
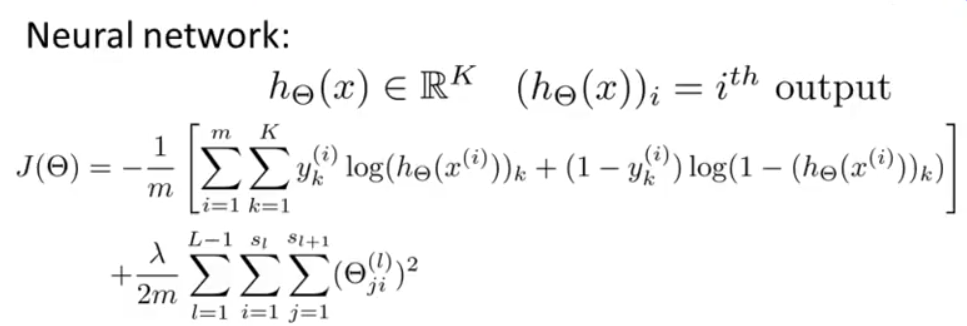
注意:
两个求和符号是将输出层每一个神经元的逻辑回归代价相加起来;
三个求和符号是将整个网络中所有参数 Θ (除去偏置单元的)的平方相加起来(下标从1开始)。
三个求和符号部分中的参数解释:
l 用于控制层数,即
二、反向传播(Backpropagation)
2.1 误差的计算
我们接下来介绍一种反向传播的算法来最小化神经网络的代价函数。
使用梯度下降或其他算法某种高级优化算法求 minΘJ(Θ) ,都需要我们自行给出 J(Θ) 和 ∂∂Θ(l)i,jJ(Θ) 的代码。
J(Θ) 我们上面已经给出了计算公式,接下来主要来看偏导项怎么求。
为了简便,我们假设只有一个训练样本 (x,y) 。
下图所示为前向传播的计算过程,我们先来看看前向传播的输出结果:

对每一个结点我们需要计算它们的误差, δ(l)j ,表示第 l 层第
上图例子中神经网络一共有4层,对于每一个输出单元( l=4 ):
其中, a(4)j 是第4层第 j 个结点的激励值,也可以写作
得到 δ(4) 以后,我们需要依次计算前面几层的误差项,计算公式如下:
这里 .∗ (element-wise multiplication )就是matlab里的点乘,指的是向量(矩阵)中的元素对应相乘。后面的 g′(z(l)) 导数项算出来的结果就是 a(l).∗(1−a(l)) 。
第一层是输入层,不会存在误差,我们并不想改变这些值,所以我们只计算到 δ(2) 。
这样,我们就通过输出层的误差 δ(4) 得到第三层的误差项,再利用第三层的误差项得到第二层的,也就是相当于我们将输出层的误差反向传播给了第三层,再传播给第二层,这就是反向传播的意思。
我们总结一下反向传播的算法。
2.2 反向传播算法描述
数据集: {(x(1),y(1)),(x(2),y(2)),⋯,(x(m),y(m))}
令 Δ(l)i,j=0 ( for all l,i,j )( Δ 是 δ 的大写形式)
对训练样本 1−m :
令 a(1)=x(i)
利用前向传播计算 a(l) ,其中 l=2,3,⋯,L ;
计算输出层(第 L 层)误差
利用反向传播计算 δ(L−1),δ(L−2),⋯,δ(2) (注意没有 δ(1) );
Δ(l)i,j:=Δ(l)i,j+a(l)jδ(l+1)i (或用向量化表示, Δ(l):=Δ(l)+δ(l+1)(a(l))T );
D(l)i,j:=1m(Δ(l)i,j+λΘ(l)i,j), if j≠0
D(l)i,j:=1mΔ(l)i,j, if j=0
D(l)i,j 即为代价函数的偏导项, ∂∂Θ(l)i,jJ(Θ)D(l)i,j 。得到偏导项的表达式后就可以将其用于梯度下降或其他的优化算法中了。
2.3 深入理解反向传播
回忆之前神经网络的代价函数:
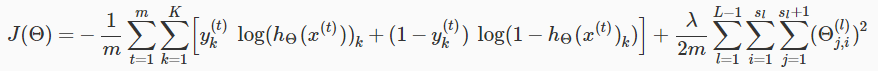
假设只有一个输出单元( K=1 )的情况,忽略正则化( λ=0 ),对于一个训练样本 (x(t),y(t)) ,则:
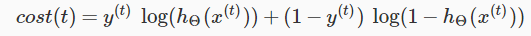
更直观来讲, δ(l)j 是 a(l)j (第 l 层第
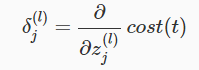
回想一下,我们的导数是与代价函数相切的直线的斜率,斜率越陡说明参数设置越不正确。
我们来看下图中的神经网络并理解如何计算
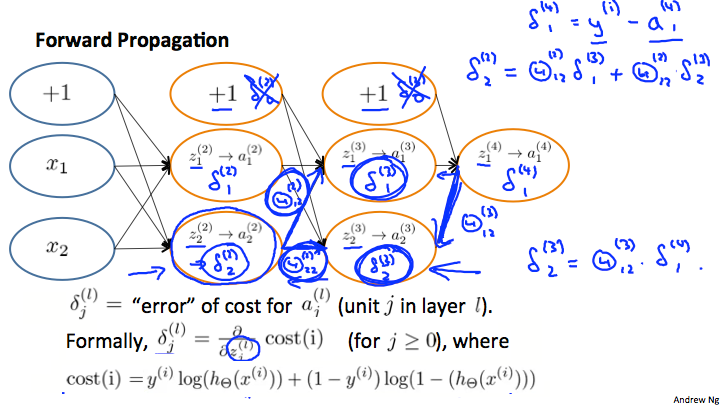
举例说明,在上图中,为了计算 δ(2)2 的值,我们将权值 Θ(2)12 和 Θ(2)22 分别与其对应的 δ 值相乘,我们得到: δ(2)2=Θ(2)12∗δ(3)1+Θ(2)22∗δ(3)2 。
如果要得到每一个 δ(l)j 的值,我们可以从右边开始计算。我们可以将每一条连接线看作参数 Θij 。从右向左,计算某一个 δ(l)j ,我们将与之右侧相连所有的权值 Θ 乘以对应的 δ 。例如: δ(3)2=Θ(3)12∗δ(4)1 。
三、反向传播算法的实践
3.1 unrolling parameter
这一部分我们会讲一个在实现中需要注意的细节,怎样将矩阵转化为向量,以便高级最优化算法中使用。
在神经网络中,我们经常会对一些矩阵进行处理:
为了能够使用优化函数,例如fminunc(),我们会将矩阵展开成一个长长的向量:
thetaVector = [ Theta1(:); Theta2(:); Theta3(:); ]
deltaVector = [ D1(:); D2(:); D3(:) ]
如果Theta1的维数为10x11,Theta2为10x11,Theta3为1x11,则可以从“展开”后的向量获取原始矩阵,如下所示:
Theta1 = reshape(thetaVector(1:110),10,11)
Theta2 = reshape(thetaVector(111:220),10,11)
Theta3 = reshape(thetaVector(221:231),1,11)
3.2 梯度检验(Gradient Checking)
利用前面所说的前向传播和后向传播计算梯度时容易出现一些小错误而不被发现,导致表面上代价函数可能在减小,但你最后得到的结果可能与实际有很大的误差,这时候就需要进行梯度检验来检验我们计算的梯度是否是我们所需要的。
这里需要提出梯度的数值估计这个概念。
如下图所示的函数:
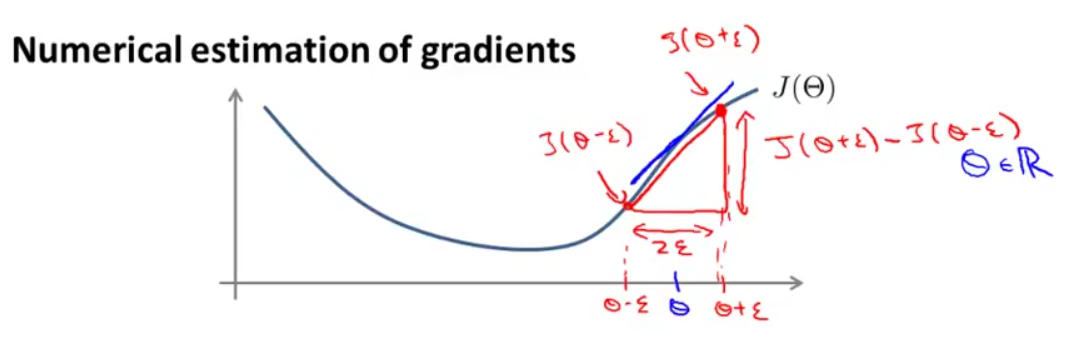
我们想得到 Θ 点函数切线的斜率(如蓝色直线),可以用红色直线的斜率来估计:
一般选用 ϵ=10−4 。
对于多个 Θ 矩阵,我们可以估计每一个 Θj 的偏导项:
octave的代码如下:
epsilon = 1e-4;
for i = 1:n,thetaPlus = theta;thetaPlus(i) += epsilon;thetaMinus = theta;thetaMinus(i) -= epsilon;gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;接下来我们要检验的就是下式是否成立:
如果成立,则说明反向传播算法是正确的。
下面总结一下需要注意的问题:

梯度检验的实现要点(步骤):
1、使用后向传播计算DVec(偏导数向量)
2、计算数值梯度的估计值gradApprox
3、确保DVec和gradApprox值相近
4、关闭梯度检验,再使用后向传播进行学习注意:在训练分类器之前一定要关闭梯度检验,如果没有关闭,则在梯度下降的每次迭代中都进行数值梯度的计算,代码运行将十分缓慢。梯度的数值估计相对于后向传播计算梯度来说是较大的工作量,我们使用数值估计的初衷仅仅是为了检验后向传播的实现是否正确。
3.3 随机初始化
运用梯度下降或者其他高级优化算法来求解 minΘJ(Θ) 时,需要对 Θ 进行初始化。
在逻辑回归中,我们可以将所有的 θ 初始化为一个全 0 的向量,但是在神经网络中我们不能这么做。
如果对于所有的
这样一来,每次更新后,两个参数 Θ 都是一样的(会得到非零的值,但是这两个值是相等的),其它参数值也是如此。
这其实相当于,当有多个隐藏单元时,所有的隐藏单元只表示同一种特征,其他完全是多余的(实际上,只要初始的 θ 值都相同,就无法破坏这种可怕的对称性)。
故神经网络对权重采用随机初始化,来破坏这种对称性。让每一个 Θ(l)ij 为 [−ϵ,ϵ] 中随机一个值(这里的 ϵ 和梯度检验里的 ϵ 不是同一个东西)。

用代码表示如下:
If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;其中 rand(10,11) 表示生成一个 10×11 的矩阵,并用 (0,1) 之间的任意数值随机初始化。
3.4 神经网络总结
1.选择一个网络结构
输入层单元数:特征 x(i) 的维数
输出层单元数:分类的类别数。
多类别分类问题输出层有多个单元,输出的 y 不是一个数了,而是由一些0 和一个 1 组成的向量。隐藏层数目:默认使用1个隐藏层,如果隐藏层数目多于1个,则每个隐藏层应该有相同的单元个数。
隐藏层单元数越多,效果越好,通常取稍大于输入特征的数目。
2.训练神经网络
构建一个神经网络,对权重随机初始化
对训练数据中任意
x(i) ,利用前向传播计算得到 hΘ(x(i))计算代价函数 J(Θ)
利用反向传播计算偏导项 ∂∂Θ(l)ijJ(Θ)
使用梯度检验比较后向传播计算得到的 ∂∂Θ(l)ijJ(Θ) 和数值估计得到的 J(Θ) 的梯度是否接近,然后关闭梯度检验。
使用梯度下降或其他高级优化算法和反向传播相结合去求解 minΘJ(Θ) ,得到最优的参数 Θ 。
对于神经网络来说, J( Theta) 是非凸函数,使用梯度下降可能得到的不是全局最小值,但这影响不大,一般来说得到的会是很小的局部最小值。
3.神经网络对新的输入分类
- 对于新的输入 x ,结合训练出的权重
Θ ,利用前向传播得到输出层的 hΘ(x) ,给出分类结果。
附课后习题答案
答案:AC

这篇关于Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 5——神经网络(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







