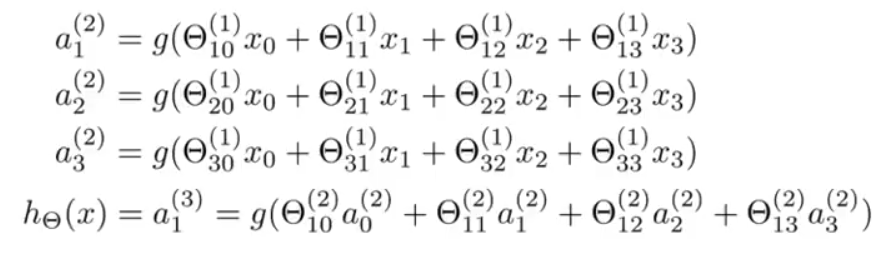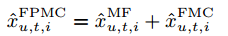本文主要是介绍Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 4——神经网络(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考)
一、前言 1.1 分类器 当我们用机器学习算法构造一个汽车识别器时,我们需要一个带标签的样本集,其中一部分是汽车,另一个部分可以是其他任何东西,然后我们将这些样本输入给学习算法,以训练一个分类器。训练完毕后,我们输入一幅新的图像,让分类器判定这是否为汽车。
1.1 神经网络的优势 对于复杂的非线性分类问题,当特征变量个数 n 很大时,用逻辑回归时 logistic 函数g ( θ T x ) θ T x 如果用二次多项式表示,则二次项数目很多,约为 n 2 ,计算复杂度达到 O ( n 2 ) ;如果用三次多项式表示,则三次项数目更多,复杂度达 O ( n 3 ) 。
而神经网络能很好的解决上面那种复杂的非线性分类问题。
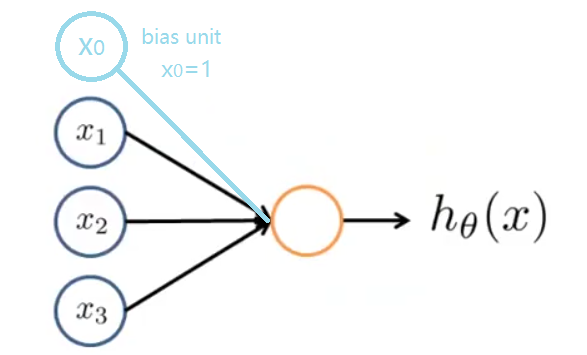
二、神经网络的模型 2.1 神经元的模型 在一个神经网络里,我们将神经元模拟成一个逻辑单元(logistic unit),如下图黄色圆圈所示。
x 1 , x 2 , x 3 是它的输入,向神经元传输一些信息,神经元通过一些计算 h θ ( x ) ,然后输出计算结果。这里, h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x 。我们称之为由logistic 函数作为激励函数的人工神经元。与前面内容相对,有时,输入单元中会加一个偏置单元 (如上图浅蓝色圆圈所示) x 0 , x 0 = 1 。
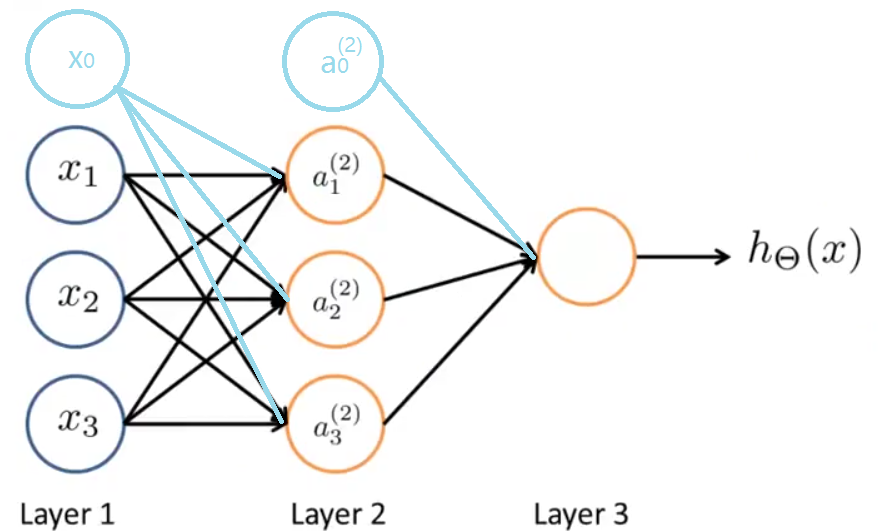
2.2 神经网络的模型 神经网络是一组神经元的组合,如下:
同样的,有时我们会加上偏置单元,它们的值永远为 1 。图中网络的第一层也叫做输入层 (Input Layer),第二层叫做隐藏层 (Hidden Layer),隐藏层可以有多层,第三层叫做输出层 (Output Layer)。
2.3 神经网络的假设函数 为了解释神经网络具体的计算步骤,我们先来说明一些符号:
a ( j ) i j 层第 i Θ j ——权重矩阵,控制着从第 j 层到第 ( j + 1 )
下面我们看一下隐藏层的神经元是怎么计算它们的值的:
如果神经网络第 j 层有 s j ( j + 1 ) 层有 s j + 1 个单元,则 Θ j 就是一个 s j + 1 ∗ ( s j + 1 ) 维的矩阵。(第 ( j + 1 ) 层的偏置单元 a ( j + 1 ) 0 不必求,始终为 1 ,但第 j ( j + 1 ) 层有影响) Θ 1 是 3 × 4 的矩阵, Θ 2 是 1 × 4 的矩阵。
三、前向传播 下面我们引入符号 z ( j ) k 来代替上面式子中括号里的部分:
a ( 2 ) 1 = g ( z ( 2 ) 1 )
a ( 2 ) 2 = g ( z ( 2 ) 2 )
a ( 2 ) 3 = g ( z ( 2 ) 3 )
总之,对于第二层的第 k 个节点:
z ( 2 ) k = Θ ( 1 ) k , 0 x 0 + Θ ( 1 ) k , 1 x 1 + ⋯ + Θ ( 1 ) k , n x n
我们用向量表示 x 和 z ( j )
x = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ x 0 x 1 ⋮ x n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ z ( j ) = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ z ( j ) 1 z ( j ) 2 ⋮ z ( j ) n ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥
根据上面的映射关系, a ( 1 ) = x ,可知:
z ( j ) = Θ ( j − 1 ) a ( j − 1 )
第 j 层激励单元的向量表示:
a ( j ) = g ( z ( j ) )
- a ( j ) 后,我们可以给第 j 层添加上偏置单元(a ( j ) 0 = 1
z ( j + 1 ) = Θ ( j ) a ( j ) , a ( j + 1 ) = g ( z ( j + 1 ) )
假设第 ( j + 1 ) 层为输出层,则:
h Θ ( x ) = a ( j + 1 ) = g ( z ( j + 1 ) )
这种从输入层的激励开始向前传播到隐藏层,再传播到输出层的行为叫做前向传播 (Forward Propagation)。
看了这么多,神经网络到底在做什么呢?
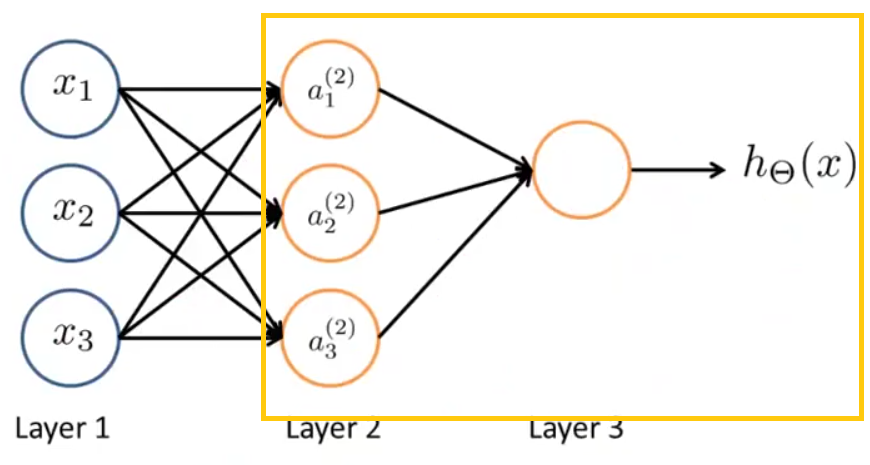
对于上面神经网络的模型那张图,如果不看输入层,只看后面两层:
写出计算公式:
h Θ ( x ) = Θ ( 2 ) 1 , 0 a ( 2 ) 0 + Θ ( 2 ) 1 , 1 a ( 2 ) 1 + Θ ( 2 ) 1 , 2 a ( 2 ) 2 + Θ ( 2 ) 1 , 3 a ( 2 ) 3
忽略一些上下标,看上去很像逻辑回归。
神经网络所做的事情很像逻辑回归,但它不是使用 x 0 , x 1 , x 2 , x 3 作为输入特征来训练逻辑回归,而是通过另一组参数 Θ ( 1 ) 将 x 0 , x 1 , x 2 , x 3 映射为隐藏层的 a ( 2 ) 1 , a ( 2 ) 2 , a ( 2 ) 3 作为输入特征。
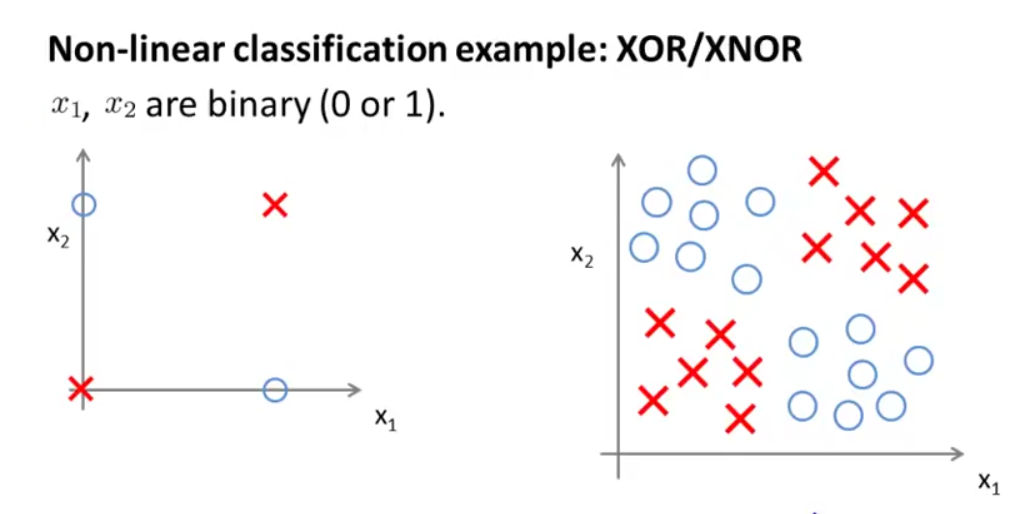
四、利用神经网络解决非线性问题 首先,我们先来看下面两张图:
如左图所示, x 1 , x 2 只能取0和1,图中只画了4个样本,我们可以把左图看做是右图的简化版本,用叉来代表正样本,圆圈代表负样本。在以前的例子中,我们会通过学习一个非线性的决策边界来区分正负样本,那么神经网络是如何做到的?
下面我们通过几个例子来看一下:
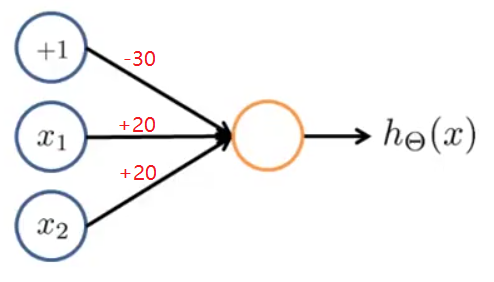
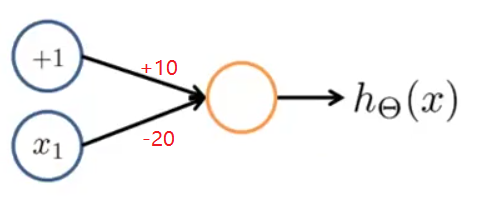
4.1 与运算(AND) x 1 , x 2 ∈ { 0 , 1 } , y = x 1 a n d x 2 ,按下图给神经网络分配权重:
h Θ ( x ) = a ( 2 ) = g ( − 30 + 20 x 1 + 20 x 2 )
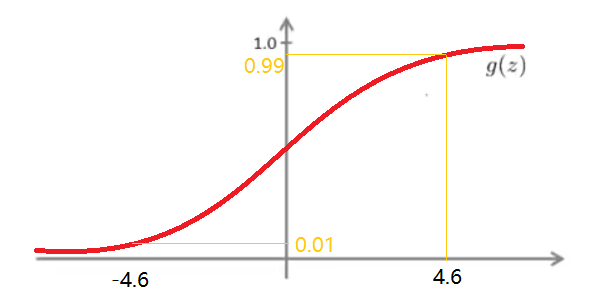
- g ( z ) 有在 z > 4.6 时越来越接近 1 ,在z < − 4.6 0 的趋势,如下图:
故我们可以得到神经网络的输出和输入的关系:
x 1 x 2 h Θ ( x ) 0 0 g ( − 30 ) ≈ 0 0 1 g ( − 10 ) ≈ 0 1 0 g ( − 10 ) ≈ 0 1 1 g ( 10 ) ≈ 1
可以看到, h Θ ( x ) ≈ x 1 o r x 2 ,该神经网络实现了与运算。
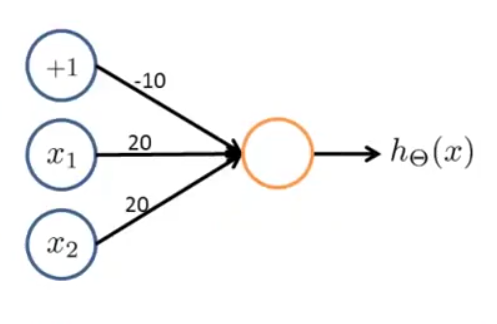
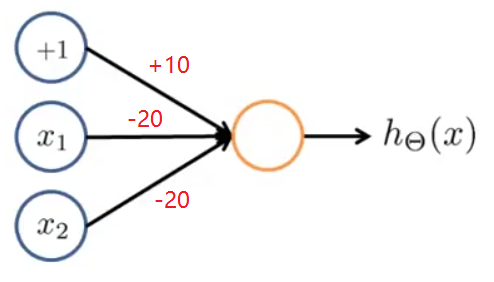
4.2 或运算(OR) x 1 , x 2 ∈ { 0 , 1 } , y = x 1 a n d x 2 ,按下图给神经网络分配权重:
h Θ ( x ) = a ( 2 ) = g ( − 10 + 20 x 1 + 20 x 2 )
画出真值表:
x 1 x 2 h Θ ( x ) 0 0 g ( − 10 ) ≈ 0 0 1 g ( 10 ) ≈ 1 1 0 g ( 10 ) ≈ 1 1 1 g ( 30 ) ≈ 1
可以看到, h Θ ( x ) ≈ x 1 o r x 2 ,该神经网络实现了或运算。
4.3 逻辑非(NOT) x 1 ∈ { 0 , 1 } , y = not x_{1}$,按下图给神经网络分配权重:
h Θ ( x ) = a ( 2 ) = g ( 10 − 20 x 1 )
画出真值表:
x 1 h Θ ( x ) 0 g ( 10 ) ≈ 1 1 g ( − 10 ) ≈ 0
可以看到, h Θ ( x ) ≈ not x_{1}$,该神经网络实现了逻辑非运算。
4.4 (NOT x 1 x 2 )
按下图给神经网络分配权重:
可以自己画真值表验证。
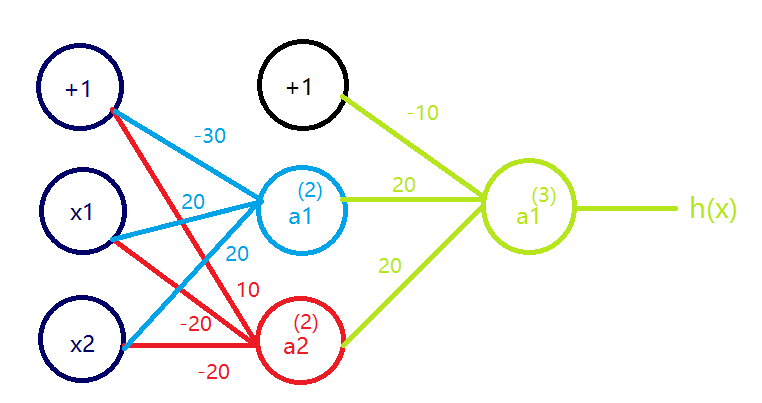
4.5 同或运算(XNOR) 按下图给神经网络分配权重:
仔细观察,可知
a ( 2 ) 1 = x 1 a n d x 2 ,即红色部分实现的是AND; a ( 2 ) 2 = ( n o t x 1 ) a n d ( n o t x 2 ) ,即蓝色部分实现的是(NOT x 1 ) AND (NOT x 2 ); h Θ ( x ) = a ( 3 ) 1 = a ( 2 ) 1 o r a ( 2 ) 2 ,即绿色部分实现的是OR;
通过真值表,我们会发现这个神经网络确实实现了同或运算(XNOR)。
通过这个例子我们可以看到,复杂函数可以通过一些简单函数的组合来实现。
比如神经网络的第二层可以计算输入层特征变量的函数;第三层可以以第二层为基础,计算更复杂的函数;第四层可以以第三层为基础计算比第三层还要复杂的函数,以此类推。神经网络运用更深的层数可以计算更复杂的函数,使其作为特征传递给最后一层的逻辑回归分类器,更准确地预测分类结果。
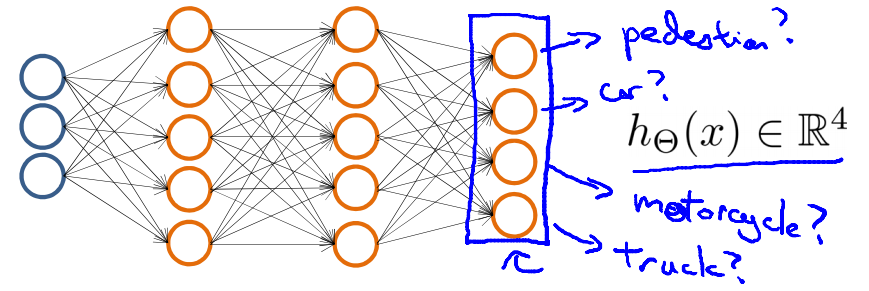
五.神经网络在多类别分类中的应用 在多类别分类中,我们的输出并不是一个数,而是一个向量,例如有一个三类别分类问题,我们要识别一个物体是行人,小汽车,摩托车还是卡车,则神经网络的模型可以如下图:
最后一层的输出层相当于有4个逻辑回归的分类器, h Θ ( x ) ∈ R 4 ,更具体的说:
训练数据集是 ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , ⋯ , ( x ( m ) , y ( 1 ) ) 。 y ( i ) 一定是上面4个列向量中的一个。神经网络的目标是使 h Θ ( x ) ≈ y ( i ) 。
相关文章
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/SCUT_Arucee/article/details/50176159 一、神经网络的代价函数
1.1 神…
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/scut_arucee/article/details/50419229 一、支持向量机的引入
1.1 从逻…
论文题目:Factorizing Personalized Markov Chains for Next-Basket Recommendation Factorizing Personalized Markov Chains for Next-Basket Recommendation
矩阵分解(MF)和马尔可夫链(MC)是推荐系统常用的两种方法…
参考资料:http://www.xuanyusong.com/archives/3278 一、生成exe运行程序以后,UI的大小如何自适应屏幕的大小
在 Canvas 的 Inspector 中设置 Canvas Scaler (Script) 的 UI Scale Mode 为 Scale With Screen Size。填写 Reference Resolution 的 X 和Y…
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/scut_arucee/article/details/50388530 一、机器学习诊断
在设计机器学…
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/quiet_girl/article/details/70842146 一、垃圾邮件分类
1.1 输入特征…
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/MajorDong100/article/details/51104784 前面提到的,对于无…
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考) 课程网址:https://www.coursera.org/learn/machine-learning 参考资料:http://blog.csdn.net/MajorDong100/article/details/51104784 一、降维的作用
1.1 数据压缩…
课程名称:CS20: Tensorflow for Deep Learning Research 视频地址:https://www.bilibili.com/video/av15898988/index_4.html#page2 课程资源:http://web.stanford.edu/class/cs20si/index.html 参考资料:https://zhuanlan.zhi…
课程名称:CS20: Tensorflow for Deep Learning Research 视频地址:https://www.bilibili.com/video/av15898988/index_4.html#page3 课程资源:http://web.stanford.edu/class/cs20si/index.html 参考资料:https://zhuanlan.zhi…
这篇关于Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 4——神经网络(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!