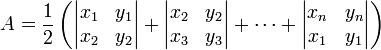此AUC非彼AUC —— 药时曲线下面积

本文主要是介绍此AUC非彼AUC —— 药时曲线下面积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

好久不见！！！因为我又火烧眉毛了一阵子！一言难尽呐！！！

祝大家一切顺利！诶！加个祝福！祝大家新的一年富得牛油！！！！！

希望我以后可以规律更新！！！！！

那这个AUC到底代表什么嘞！快来跟我一起看看吧！！！

定义

在药物动力学中，AUC（area under the plasma concentration-time curve），也就是药时曲线下面积，通常指的是药物在体内浓度与时间之间的曲线下面积。
图片来源：维基百科 - [https://zh.wikipedia.org/wiki/曲线下面积_(药物代谢动力学)

药物浓度-时间曲线：这个曲线反映了药物在一段时间内的浓度变化。AUC 的计算是基于测量药物在血浆中的浓度随时间的变化。通过在不同时间点采集血样并测定药物浓度，可以绘制血浆浓度-时间曲线。

AUC 取决于药物的剂量和药物的清除速率。剂量越大，AUC 就越高。药物的清除速率越慢，AUC 就越高，因为药物在体内停留的时间更长。

那么为什么AUC可以表示药物血液系统的量呢！我找来了一篇超详细的解答，希望对大家有帮助！

原文链接：https://zhidao.baidu.com/question/1732619638652694347.html

先解释下对于常见的口服药物药时曲线的意义和特征及其特性！

首先对于一个口服的药物来说，它是同时存在吸收过程（即药物以分子或者离子形态透过胃肠道细胞膜进入血液循环系统）以及消除过程，这里假设药物一旦进入血液后就能够迅速的分布并且就开始产生了接下来的消除过程，一般来说这个现象是可以这么解释的，对于一个口服的药物来说，其达到峰值的浓度时间 $T_{max}$ 通常要大于 1h 以上，而药物在血液的速度是很快的，所以可以认为接近瞬时分布！这是第一点！

第二点，要明白为什么对于口服药物来说药时曲线先上升后下降。这主要是因为一开始口服药物吸收速度最快，但是这个时候再血液里的量却是最少的，所以消除几乎不计，随着药物进一步的吸收，虽然说吸收速度会减慢，这个时候药物在体内是逐渐聚集的过程，而消除的速度也由于药物血药浓度的增加而随着增大，然后等到吸收进一步进行到了某一个程度时刻时，口服药物的吸收速度刚好等于该时刻血液中药物的总体消除速度，这个时候就到了一个转折点，也就是上面所说的最大血药浓度的时间 $T_{max}$ ，而过了 $T_{max}$ 后，吸收还是原动力，其继续进行，其速度只跟胃肠道中药物的总量有关，这时候吸收的速度进一步减慢，而消除则相应的呈现出占主导的地位，所以消除的速度大于吸收的速度，这个时候曲线开始向下走，最后药物基本被吸收完后，然后药时曲线就基本走平啦！

这里，不难看出其实真正意义上教材上讲“药物进入血液系统的量”包含两层意思：第一层药物通过生物膜进入血液的量（这个不包括消除的部分），但是第一这个量很难计算，第二其实没多大必要关心药物真正进入多少量，因为不管进入多少量，但是如果速度有差别的话，其在体内的生物作用还是有差别的！而另一层意思就是指口服服用后在血液循环中实际存在的量或者说是实际的作用效果，因为本质上不管是什么药物都有时效性的。再举一个简单的比喻，如物理学上，力和冲量的关系一样，这个量其实不是单纯的质量，而是冲量的意思，也就是效应！所以说药时曲线下面积（AUC）其本质上还是能反应药物实际进入血液系统中的量（上面说的一样，这个是实际的作用效果，而且也正是需要 AUC 这种描述来表达）！

所以说 AUC 这个概念还是非常实用的，其实具体进入血液多少量不是重点，因为还有进入的速度有影响，同时消除也跟着变化，所以为了真正考察一个口服药物的作用，采用 AUC 这个指标是最好不过啦，它是综合口服吸收的速率及程度以及在体内动态消除的综合结果，是一个综合反映口服制剂到底在体内有多少作用效应的关键的量值！

最后总结下，为什么使用 AUC，首先由于口服药物在胃肠道中肯定有其他干扰，所以最终吸收的量肯定不同，那为什么不直接用其他指标来直接测量药物进入机体多少量呢？因为药物进入体内是有时间的，通常需要 2 个小时以上，同时药物在体内是有是失效的也就是要消除，所以说单纯测定实际进入多少量反而不能来解决要解决的问题！所以采用了一个很好的方法，AUC！用它综合表示药物进入血液系统的量！

计算方法

AUC的具体计算方法通常涉及对浓度-时间曲线的积分。下面是一个简化的表达式：

$\int_{t_1}^{t_2} C(t) \,dt$

其中：

$A U C$ 表示曲线下的面积，即 $A U C$ 。
$C (t)$ 表示在时间 $t$ 处的药物浓度。
$t_1$ 和 $t_2$ 表示观察时间的起始和结束点。

上面这种算法属于是一种理想情况，也就是说如果浓度是连续的，AUC就可以通过实际积分来计算。在这种情况下，积分的上下限就是观察时间的起始和结束点。

而具体计算 $A U C$ 的方法取决于实际的测量数据和采样时间点。在离散的时间点上，可以使用数值积分方法，例如梯形法则或辛普森法则。

梯形法则

如果浓度在离散的时间点上测量， $A U C$ 可以近似为梯形面积之和。其计算公式为：

$\frac{1}{2} \sum_{i=1}^{n-1} (C_{i} + C_{i+1}) \cdot (t_{i+1} - t_{i})$

其中 $n$ 表示采样点的数量， $C_i$ 表示在时间点 $t_i$ 处的浓度。

从计算公式可以看出，AUC 的单位应是“浓度 × 时间”。浓度的单位可以是质量浓度也可以是物质的量浓度；时间可以是任意时间单位，如小时(h)、分(min)等。浓度与时间的具体单位，可以随意选取，往往是人为设定的。

需要注意的是，这只是一个简化的表达式，实际计算可能还需要考虑其他因素，例如药物在体内的消除和分布等。具体的计算方法可能取决于具体的研究和实验设计。

辛普森法则

辛普森法则是用于近似连续函数积分的数值积分方法。对于 $A U C$ 的计算，我们可以将血浆浓度-时间曲线视为一个连续函数，然后使用辛普森法则来估计曲线下的面积。

下面是辛普森法则的具体公式，适用于等间隔的时间点 $t_0, t_1, \ldots, t_n$ 上的浓度值 $C_0, C_1, \ldots, C_n$ ：

$\approx \frac{h}{3} \left[ C_0 + 4C_1 + 2C_2 + 4C_3 + \ldots + 2C_{n-2} + 4C_{n-1} + C_n \right]$

其中：

$h$ 是每个时间间隔的宽度，可以通过 $\frac{t_n - t_0}{n}$ 计算，其中 $t_n$ 和 $t_0$ 分别是曲线的结束和起始时间点。
$n$ 是等间隔时间点的数量，通常为偶数。
$C_i$ 是在时间点 $t_i$ 处的浓度值。

辛普森法则的优势在于它对于连续函数的曲线拟合较好，相对于梯形法则，它通常提供更准确的积分结果，特别是在曲线变化剧烈的地方。

“特别是在曲线变化剧烈的地方” 表示辛普森法则相对于梯形法则在处理曲线上急剧变化的区域时更为精确。

考虑一个血浆浓度-时间曲线，假设在某些时间点附近存在急剧的浓度变化。在这种情况下，梯形法则将使用线性插值来连接相邻的时间点，可能无法很好地捕捉到这种急剧变化的特性。梯形法则在对这种曲线进行积分时可能会产生一定的误差。

辛普森法则通过使用二次插值（抛物线）来更好地适应连续函数，因此在曲线变化较大的地方，辛普森法则通常能够提供更准确的积分结果。这种精度优势尤其在曲线存在弯曲、峰值或谷底等形态特征时更为显著。

所以呀，辛普森法则对于复杂曲线的积分更为适用，尤其是在曲线存在急剧变化的区域。

辛普森法则的公式中的数字 2 和 4 是用于计算每个小区间面积权重的系数。这些系数是通过将每个小区间视为一个抛物线来得到的，而这个抛物线的系数决定了在辛普森法则中的权重。

辛普森法则使用以下权重系数：

中间的奇数项：4
两端的偶数项：2
第一个和最后一个项：1

所以，在计算 $A U C$ 的时候，每个小区间的贡献被加权，中间的奇数项占据主导地位，而两端的偶数项则辅助调整权重，以更好地逼近曲线的形状。

辛普森法则的公式可以表示为：

$\approx \frac{h}{3} \left[ y_0 + 4y_1 + 2y_2 + 4y_3 + \ldots + 2y_{n-2} + 4y_{n-1} + y_n \right]$

其中，系数 4 和 2 就是用于调整对应位置浓度值 $y_i$ 的权重，使得曲线下的面积更准确地估计。

常见相关参数

$A U C$ ： $A U C$ 表示什么相信大家已经知道啦！不知道的罚你返回去再读一次！（不敢不敢哈哈哈哈哈哈哈哈） $A U C$ 取决于药物的剂量和药物的清除速率。剂量越大， $A U C$ 就越高。药物的清除速率越慢， $A U C$ 就越高，因为药物在体内停留的时间更长。
$C_{\text{max}}$ （最大浓度）：表示在给定剂量下达到的最大血浆浓度。 $C_{max}$ 取决于药物的剂量和吸收速度，剂量越大或吸收速度越快， $C_{max}$ 就越高。
$T_{\text{max}}$ （最大浓度的时间）：表示在给定剂量下达到最大浓度的时间点。 $T_{\text{max}}$ 取决于药物的吸收速度，吸收速度越快， $T_{\text{max}}$ 就越短，与药物的消除速率无关。
$C_{\text{min}}$ （最小浓度）：表示在给定剂量下的最小血浆浓度。
$T_{\text{min}}$ （最小浓度的时间）：表示在给定剂量下达到最小浓度的时间点。
半衰期：半衰期取决于药物的消除速率。药物消除速率越慢，半衰期就越长。半衰期与 $T_{max}$ ， $C_{max}$ 和 $A U C$ 无关。

这些都是反映药物吸收、分布和消除的重要药代动力学参数。它们相互独立，但也存在某些关联。

为什么AUC可以代表药物疗效

AUC 并不直接代表药物的治疗效果，而是在一定程度上反映了药物的曝露程度。为了更好地理解为什么AUC被认为与药物效果相关，我们可以从以下几个方面进行考虑：

曝露程度： AUC 表示药物在给定时间内对体内的总体曝露程度。更大的 AUC 通常表示更高的曝露水平，即更长时间内更高的药物浓度。这对于一些药物而言，特别是需要维持一定疗效浓度的药物，是关键的。
剂量-反应关系： AUC 与剂量-反应关系密切相关。在药物疗效的剂量-反应曲线中，AUC 是剂量与反应之间的综合指标，可以反映出药物对生物体的整体效应。较大的 AUC 通常与更好的治疗效果相关联。
药代动力学参数： AUC 是许多药代动力学参数的基础，如清除率、生物利用度和半衰期。这些参数与药物在体内的动态过程相关，对于理解药物在体内的行为和调整治疗方案至关重要。
个体化治疗： AUC 可以用于个体化治疗，通过比较不同个体的 AUC 值，可以确定适当的药物剂量，以确保在体内达到期望的治疗效果所需的药物浓度。

需要注意的是，虽然 AUC 提供了对药物在体内曝露的综合性评估，但并不是唯一的评估标准。药物的疗效还可能受到其他因素的影响，包括药物的靶点、药物在目标组织中的分布、药物的药理学性质、患者的个体差异、疾病状态等等等等。因此，在综合评估药物效果时，我们通常需要结合多个指标和参数。

为什么我选择使用AUC而不是IC50/EC50

AUC 和 IC50、EC50 等指标是用于不同目的的药物评价指标，它们分别在药物动力学和药效学的领域有不同的应用。

AUC（药物动力学）

AUC 表示药物在体内的总曝露程度，考察的是血药浓度随时间的变化，是药物在体内的动力学特性之一。它对于描述整体的药物曝露效果较为有用，主要用于评估药物在体内的吸收、分布、代谢和排泄等过程，以确定药物的动力学特性，指导合理用药和调整剂量。因此，AUC 在比较不同药物或不同给药途径时很有价值。
IC50 和 EC50（药物药效学）
- **IC50（Inhibitory Concentration 50%）：**半数抑制浓度，IC50用于衡量抑制生物学效应的浓度，通常用于评估药物对生物学活性的抑制程度。IC50 表示药物在体外或细胞培养中使生物体对某种生物学过程的反应降低一半所需的浓度。在生物学和药物筛选中，IC50 常用于比较不同药物或化合物的相对抑制效力。
- **EC50（Effective Concentration 50%）：**半数最大效应浓度，EC50 用于测量生物效应的浓度，使生物效应达到最大效应的一半。它通常用于评估激动剂或激动剂类药物对生物系统的效应，研究药物与生物体相互作用的效应浓度，如药物对酶的抑制或对受体的激活等。EC50 在生物学和药理学研究中用于比较药物的效能。

在选择这些指标时，需要考虑实验的具体情境和研究问题。例如，如果你关注的是整体药物曝露的效果，AUC 可能更合适；如果你关注的是药物对生物学活性的抑制，IC50 可能更为适用；而如果你研究的是激动剂的效应，EC50 可能是更合适的选择。实际应用中，这些指标有时也可以结合使用，以提供更全面的信息。

我选择使用 AUC 而不是 IC50 / EC50 的原因包括：

**全面性：**AUC 综合了药物在体内的吸收、分布、代谢和排泄等多个因素，提供了对整个药物动力学过程的综合性评估。相比之下，IC50 和 EC50 更侧重于药效学的一方面，即药物与生物体相互作用的效应浓度。
**临床相关性：**AUC 与药物在体内的总体曝露程度相关，更符合临床实际应用的需要。在实际治疗中，医生更关心药物在患者体内的总体效果，而不仅仅是在细胞培养条件下的效应浓度。
**动态性：**AUC 考虑了药物在不同时间点的浓度变化，因此更适用于描述药物在体内的动态过程。IC50和EC50通常是在某个特定时间点或条件下测得的值，不能全面反映药物的时效性。

当然，这只是我自己的选择！大家可以随意！最后这段描述呢！我就是单纯想把自己的想法顺便记录下来！如果大家觉得哪里不合适或者有其他建议的话，欢迎随时探讨！！！

我们下期再见哟！

如果我的分享对你有用的话，欢迎关注点赞在看转发分享阿巴阿巴阿巴阿巴巴巴！这可是我的第一原动力！

蟹蟹你们的喜欢和支持！！！

啊对！如果小伙伴们有需求的话，也可以加入我们的交流群：一定要知道 | 我们的生信交流群终于来啦！