本文主要是介绍【论文笔记】Solving Billion-Scale Knapsack Problems,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Solving Billion-Scale Knapsack Problems
Ant Financial Services Group, San Mateo, CA 94402
简化速读
对组合优化问题进行拉格朗日对偶,进而可以拆分成子问题,如果给定乘子 λ \lambda λ则子问题比较容易解决,且可以并行计算。
求解乘子 λ \lambda λ可以采用对偶下降(dual descent ,DD)或者同步坐标下降(SCD)。对偶下降法比较简单,就是 λ k t + 1 = m a x ( λ k t + α ( ∑ i , j b i , j , k x i , j − B k ) , 0 ) \lambda_k^{t+1}=max(\lambda_k^{t}+\alpha(\sum_{i,j}b_{i,j,k}x_{i,j}-B_k),0) λkt+1=max(λkt+α(∑i,jbi,j,kxi,j−Bk),0),缺点是超参数 α \alpha α不好设定;同步坐标下降则是利用内点法计算所有可能改变解( x i , j x_{i,j} xi,j)的 λ \lambda λ的值:然后在reduce阶段选取不违反全局约束的最小的 λ \lambda λ。
两个trick,一个是初始化,可以用均匀采样的小数据量快速解一个初始值,这样在全量数据能够减少40%到70%的迭代次数;第二个是后处理,如果轻微的违反的约束,可以按 p ~ i j \tilde{p}_{ij} p~ij大小排序,从小往大删除来使得约束得到满足。
全文
ABSTRACT
背包问题(Knapsack problems,KPs)在工业中很常见,但求解KPs是NP-hard问题,只能在较小的规模下求解。本文以一种稍微广义的形式研究了KPs,并证明通过分布式算法可以近似最优地求解KPs。提出的方法可以在现成的分布式计算框架(如MPI、Hadoop、Spark)中很容易地实现。本文的实现带来了迄今为止已知最高效的KP求解器之一——能够求解前所未有的规模KP(具有10亿决策变量和10亿约束的KP可以在1小时内求解)。该系统已部署到生产环境中,每天都会被调用,对Ant Financial产生重大的业务影响。
1 INTRODUCTION
背包问题(KPs)常见于现实应用中,例如预算分配和调整(如广告和营销)、在线流量控制(如搜索引擎和推荐系统)、物流优化(如电子商务)、资产管理(如金融)等。不幸的是,求解KPs是众所周知的NP-hard问题,并且在实践中只有在相对较小的规模下才是可行的,即使是商业求解者。
主要动机是在互联网行业中经常出现KPs,在这种情况下,需要在每个用户的基础上做出决定,而用户数量可能很大(例如数十亿)。KP中要分配的“资源”可以是财务的(如贷款、营销推广、广告支出、资产组合)或非财务的(如用户印象、点击、停留时间)。通常,我们希望在一组约束条件下优化目标(例如,在营销活动中的预期用户转换),这些约束条件大致可以分为两类:一类是全局约束条件,通常在全局级别上限制资源的最大允许量,以及对个别用户/用户组施加进一步限制的局部限制。实际上,虽然全局约束的规模通常很小(例如几百个),但是决策变量和局部约束的典型规模都可以达到数十亿级。不幸的是,在这样的规模下解决KPs是一个公开的技术挑战。
本文是解决现实世界十亿级KPs的首次尝试之一。首先,利用MapReduce计算模型,利用对偶问题(dual problems)和对偶下降(dual descent ,DD)的可分解性,设计了一个求解KPs的分布式框架。其次,为了进一步提高算法的收敛性,特别是当DD算法在分布式环境中实现时容易出现约束冲突时,我们开发了不受这些问题影响的同步坐标下降(SCD)算法。此外,利用局部约束的层次结构,我们证明了贪婪算法可以在多项式时间内优化求解整数规划子问题,极大地提高了具有层次局部约束的KPs的求解质量和速度。最后,我们使用现成的分布式计算框架(如MPI、Hadoop、Spark)来实现我们的算法,从而获得迄今为止最有效的KP求解器之一(例如,具有10亿个决策变量和10亿个约束的KP可以在1小时内求解)。本文的工作已经部署到生产环境,用于蚂蚁金融每天的生产决策。
2 PROBLEM FORMULATION
考虑背包问题的广义变体(公式(1)–(4)),其中在 K K K个全局约束和 L L L个局部约束下,一组 M M M个item将被分配给一组N个用户。全局约束(公式(2))限制每个背包的资源分配,而局部约束(公式(3))限制每个用户的消耗。如果 item j 被分配给 group i,即 x i , j = 1 x_{i,j}=1 xi,j=1,增加了 p i . j p_{i.j} pi.j的收益,并且消耗第 k k k个背包 b i , j , k b_{i,j,k} bi,j,k的资源量( k ∈ [ K ] = { 1 , 2 , . . . , K } k\in [K]=\{1,2,...,K\} k∈[K]={1,2,...,K})。 B k B_k Bk和 C l C_l Cl严格为正, p i , j p_{i,j} pi,j和 b i , j , k b_{i,j,k} bi,j,k为非负。
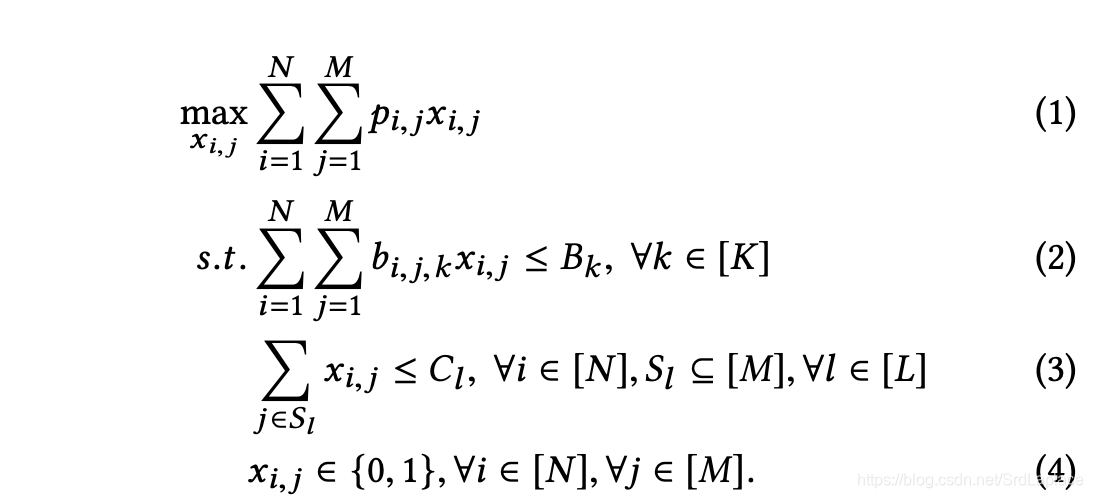
注意,虽然我们假设 x i , j x_{i,j} xi,j是binary(即 x i , j ∈ { 0 , 1 } x_{i,j}\in \{0,1\} xi,j∈{0,1}),但是本文的方法同样适用于categorical变量。
2.1 Hierarchical Local Constraints
进一步探讨(1)–(4)更复杂情况,其中在局部约束(3)中存在层次结构,使得索引集不相交或嵌套。
Definition 2.1. 当以下情况成立时,局部约束(3)称为Hierarchical(层级的): ∀ l . l ′ ∈ [ L ] , i f S l ∩ S l ′ ≠ ∅ ⇒ S l ⊆ S l ′ o r S l ′ ⊆ S l \forall l.l'\in [L], if~S_l\cap S_{l'}\neq \empty \Rightarrow S_l\subseteq S_{l'}~or~S_{l'}\subseteq S_l ∀l.l′∈[L],if Sl∩Sl′=∅⇒Sl⊆Sl′ or Sl′⊆Sl
这种特性在现实世界中很常见,在现实世界中,items之间不是相互独立的,而是相互关联的。对于 { S l ∣ l ∈ [ l ] } \{S_l | l∈[l]\} {Sl∣l∈[l]}可以构造有向无环图。在items无关的情况下,这个DAG将退化为一个集,其中 S l S_l Sl彼此不相交。
2.2 Connections to Other KP Variants
一些文献研究了背包问题的几种变体,包括多维背包问题(multi-dimensional knapsack problems, MDKPs)、多选择背包问题(multi-choice knapsack problems, MCKPs)和多维多选择背包问题(multidimensional multi-choice knapsack problems, MMKPs)。MDKP是一个item和多个背包约束,当item被选择时,将消耗来自多个背包的资源。MCKP是经典的单约束KP的一个扩展,它将item划分为多个组,每个组只能选择一个项目。MMKP是MDKP和MCKP的组合。
公式(1)–(4)的形式是比较灵活的约束形式。事实上,所有这些经典背包问题变体都可以看作是公式的特例。例如,当 M = 1 M=1 M=1和 L = 0 L=0 L=0时,为MDKPs;当 K = 1 , C = 1 K=1,C=1 K=1,C=1和 L = 1 L=1 L=1时,为MCKPs;当 C = 1 C=1 C=1和 L = 1 L=1 L
这篇关于【论文笔记】Solving Billion-Scale Knapsack Problems的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








