WhaleQuant第四章——量化选股策略

本文主要是介绍WhaleQuant第四章——量化选股策略，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第四章

4.0 学习资源

学习链接

1. 市场有效性理论：

• 描述了证券市场的四种有效性类型：无效市场、弱式有效市场、半强式有效市场和强式有效市场。
• 讨论了有效市场理论对投资者选股策略的影响，特别是在短期和长期市场中，市场无效性可能为投资者提供超额收益的机会。

2. 效用模型与风险模型：

• 介绍了效用函数（Utility Function）和期望效用假说（Expected Utility Hypothesis），以及它们在投资者决策中的应用。
• 讨论了损失厌恶（Loss Aversion）现象，即投资者对损失的厌恶程度大于对同等金额收益的喜好。

3. 现代资产配置理论（MPT）：

• 描述了MPT的核心思想，即通过最小化标准差并最大化预期收益来进行资产配置。
• 解释了有效前沿（Efficient Frontier）、夏普比率（Sharpe Ratio）和资本市场线（Capital Allocation Line）的概念。

4. 资本资产定价模型（CAPM）：

• 介绍了CAPM模型，它基于MPT，描述了资产收益率与市场风险之间的关系。
• 讨论了系统性风险（Systematic Risk）和非系统性风险（Unsystematic Risk）的区别。

5. 套利定价理论（APT）与多因子模型：

• APT模型将资产收益归因于多个因子，而不仅仅是市场风险。
• 多因子模型（MFM）是APT模型的扩展，它通过多个因子来解释股票的预期收益。

6. 量化因子构建：

• 介绍了基于日频数据和高频数据的量化因子构建方法。
• 讨论了如何通过计算机语言来描述和实现量化计算过程。

7. 因子有效性检验：

• 介绍了如何通过统计方法（如p值）来检验因子的有效性。
• 讨论了市值中性化和行业中性化的概念，以及它们在因子分析中的应用。

8. 多因子选股模型实践：

• 提供了一个使用Python实现的简单多因子选股模型示例，该模型通过线性回归来预测股票收益，并根据预测结果选择股票。
• 这一章节为投资者提供了一套系统的方法论，用于在量化投资中构建和评估选股策略。通过理解和应用这些理论，投资者可以更科学地进行资产配置，提高投资决策的效率和效果。

4.1 行业与市值中性化——程序1

import numpy as np
import pandas as pd
import statsmodels.api as sm# 假设我们有一个包含市值因子和收益的数据框 DataFrame
# 数据框的列包括：'日期'、'股票代码'、'市值'、'收益'等# 假设我们已经从数据源加载了数据，存储在变量 data 中# 选择所需的列
data = data[['日期', '股票代码', '市值', '收益']]# 根据日期进行分组
groups = data.groupby('日期')# 定义一个函数来执行市值中性化
def market_neutralize(group):# 提取市值和收益的数据列market_cap = group['市值']returns = group['收益']# 添加截距项X = sm.add_constant(market_cap)# 执行线性回归，拟合收益率与市值的关系model = sm.OLS(returns, X)results = model.fit()# 提取回归系数beta = results.params['市值']# 计算市值中性化后的收益neutralized_returns = returns - beta * market_cap# 将市值中性化后的收益添加到数据框中group['市值中性化收益'] = neutralized_returnsreturn group# 对每个日期的数据进行市值中性化
neutralized_data = groups.apply(market_neutralize)

但这段代码缺少data数据。下面重新写一个获取数据的版本，并且字段为英文：

import baostock as bs
import pandas as pd
import statsmodels.api as sm
from IPython.display import display# 登陆系统
lg = bs.login()
# 显示登陆返回信息
print('login respond error_code:'+lg.error_code)
print('login respond error_msg:'+lg.error_msg)# 获取股票数据
rs = bs.query_history_k_data_plus("sh.600000","date,code,close,volume",start_date='2022-07-01', end_date='2022-12-31',frequency="d", adjustflag="3")
print('query_history_k_data_plus respond error_code:'+rs.error_code)
print('query_history_k_data_plus respond error_msg:'+rs.error_msg)# 将获取的数据转为DataFrame
data_list = []
while (rs.error_code == '0') & rs.next():data_list.append(rs.get_row_data())
data = pd.DataFrame(data_list, columns=rs.fields)# 选择所需的列
data = data[['date', 'code', 'close', 'volume']]# 根据日期进行分组
groups = data.groupby('date')# 定义一个函数来执行市值中性化
def market_neutralize(group):# 提取市值和收益的数据列market_cap = group['close'].astype(float)returns = group['volume'].astype(float)# 添加截距项X = sm.add_constant(market_cap)# 执行线性回归，拟合收益率与市值的关系model = sm.OLS(returns, X)results = model.fit()# 提取回归系数beta = results.params['close']# 计算市值中性化后的收益neutralized_returns = returns - beta * market_cap# 将市值中性化后的收益添加到数据框中group['market_neutralized_volume'] = neutralized_returnsreturn group# 对每个日期的数据进行市值中性化
neutralized_data = groups.apply(market_neutralize)# 打印市值中性化后的数据
display(neutralized_data)# 登出系统
bs.logout()

将结果绘制出来（将因子放大1e9倍显示）：

import seaborn as sns
import matplotlib.pyplot as plt# 使用 pivot 方法来重塑数据
transposed_data = neutralized_data.pivot(columns='code', values='market_neutralized_volume')
# 将数据放大1e9倍
transposed_data *= 1e9
# 使用 seaborn 绘制热图
plt.figure(figsize=(12, 20))
sns.heatmap(transposed_data, cmap='coolwarm', linewidths=0.5, annot=True, fmt=".2f")
plt.title('Market Neutralized Volume')
plt.xlabel('Stock Code')
plt.ylabel('Date')
plt.show()

4.2 Python多因子选股策略实践

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split# 生成随机数据
np.random.seed(42)
n_samples = 1000data = {'PE': np.random.uniform(5, 20, n_samples),'PB': np.random.uniform(0.5, 3, n_samples),'ROE': np.random.uniform(0.05, 0.25, n_samples),'Returns': np.random.normal(0.1, 0.5, n_samples)
}df = pd.DataFrame(data)# 保存生成的数据到 CSV 文件
df.to_csv('stock_data.csv', index=False)# 读取和准备数据
df = pd.read_csv('stock_data.csv')
X = df[['PE', 'PB', 'ROE']]  # 特征因子
y = df['Returns']  # 目标变量# 拆分训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 标准化处理
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 构建线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)# 查看模型系数，确定因子权重
print('Factor weights:', model.coef_)# 使用模型预测测试数据的收益
y_pred = model.predict(X_test)# 创建一个 DataFrame 来存储股票的预测收益
predicted_returns = pd.DataFrame({'Stock': pd.RangeIndex(start=0, stop=len(X_test)),'Predicted return': y_pred
})# 根据预测的收益选择股票
selected_stocks = predicted_returns[predicted_returns['Predicted return'] > 0.1]print('Selected stocks:', selected_stocks)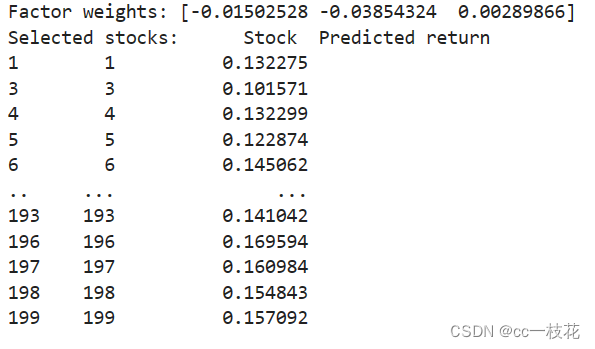

这篇关于WhaleQuant第四章——量化选股策略的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---