本文主要是介绍【算法】走廊泼水节(最小生成树,完全图),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
给定一棵 N 个节点的树,要求增加若干条边,把这棵树扩充为完全图,并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。
注意: 树中的所有边权均为整数,且新加的所有边权也必须为整数。
输入格式
第一行包含整数 t,表示共有 t 组测试数据。
对于每组测试数据,第一行包含整数 N。
接下来 N−1 行,每行三个整数 X,Y,Z,表示 X 节点与 Y 节点之间存在一条边,长度为 Z。
输出格式
每组数据输出一个整数,表示权值总和最小值。
每个结果占一行。
数据范围
1≤N≤6000
1≤Z≤100
输入样例:
2
3
1 2 2
1 3 3
4
1 2 3
2 3 4
3 4 5
输出样例:
4
17 思路
从小到大依次遍历所有树边,若遍历到连接团N与团M的树边长为w,需要添加(N * M)- 1条长为w + 1的边使连接之后的团成为完全图。如下图所示:

关键代码如下:
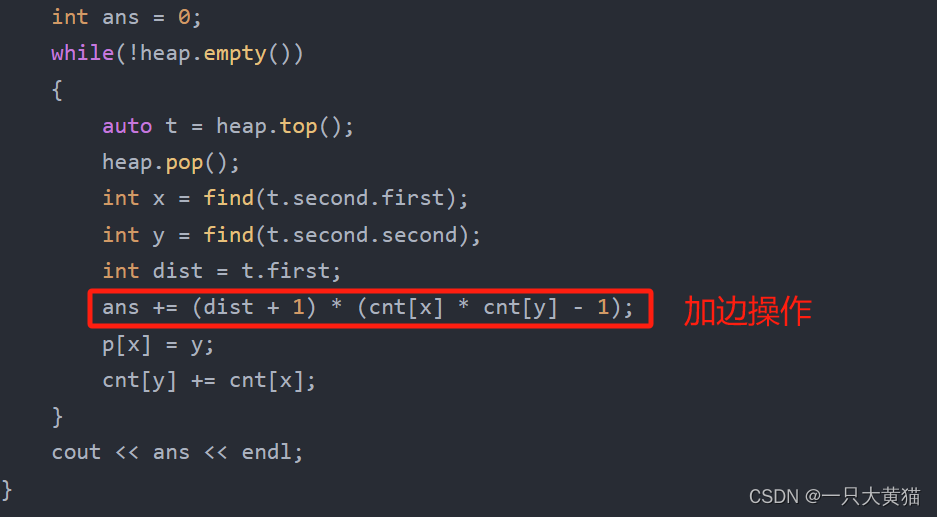
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 6e3 + 10;
typedef pair<int,pair<int,int>> PII;
int n;int p[N];
int cnt[N];int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}void solve()
{cin >> n;for(int i = 1; i <= n; i ++) p[i] = i,cnt[i] = 1;priority_queue<PII,vector<PII>,greater<>> heap;for(int i = 1; i < n; i ++){int x,y,dist;cin >> x >> y >> dist;heap.push({dist,{x,y}});}int ans = 0;while(!heap.empty()){auto t = heap.top();heap.pop();int x = find(t.second.first);int y = find(t.second.second);int dist = t.first;ans += (dist + 1) * (cnt[x] * cnt[y] - 1);p[x] = y;cnt[y] += cnt[x];}cout << ans << endl;
}int main()
{int t;cin >> t;while(t --)solve();return 0;
}| 难度:中等 |
| 时/空限制:1s / 64MB |
| 总通过数:6735 |
| 总尝试数:10984 |
| 来源:《算法竞赛进阶指南》 |
| 算法标签 图论 最小生成树 Kruskal |
题目来自:346. 走廊泼水节 - AcWing题库
这篇关于【算法】走廊泼水节(最小生成树,完全图)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




