GDPU 数据结构 天码行空13

一、【实验目的】

(1) 理解插入排序算法的实现过程；

（2）理解不同排序算法的时间复杂度及适用环境；

（3）了解算法性能测试的基本方法。

二、【实验内容】

1、以下是一个通过随机数来测试排序算法运行时间的程序，中间留出了加入排序算法的部分。其中可以通过修改RANDNUM的值来更改测试的数据量:

#include "stdio.h"
#include <stdlib.h>
#include <time.h>
#define RANDNUM 10000 //随机数的个数
void main（）
{ int iRandNum[RANDNUM];//存放随机数clock_t first，second; //记录开始和结束时间（以毫秒为单位）int i;for（i=0;i<RANDNUM;i++）{//产生1万个随机数iRandNum[i]=rand（）%RANDNUM;}first=clock（）; //开始时间//此处加入排序程序second=clock（）;//结束时间//显示排序算法所用的时间
}

2、从选择、交换、插入排序算法中任选至少3种排序算法（希尔排序、快速排序、堆排序三选二），在无序状态下进行多次运行，记录运行时间，并比较测试结果。
提示:在程序的实现过程中要用到以下函数，请大家在实验之前自学这几个函数的用法:

1）随机函数rand（）

2. 时间函数clock（）

实验参考界面如下（此界面测试数据仅选用了两种算法，提交的报告以实验要求为准。）:

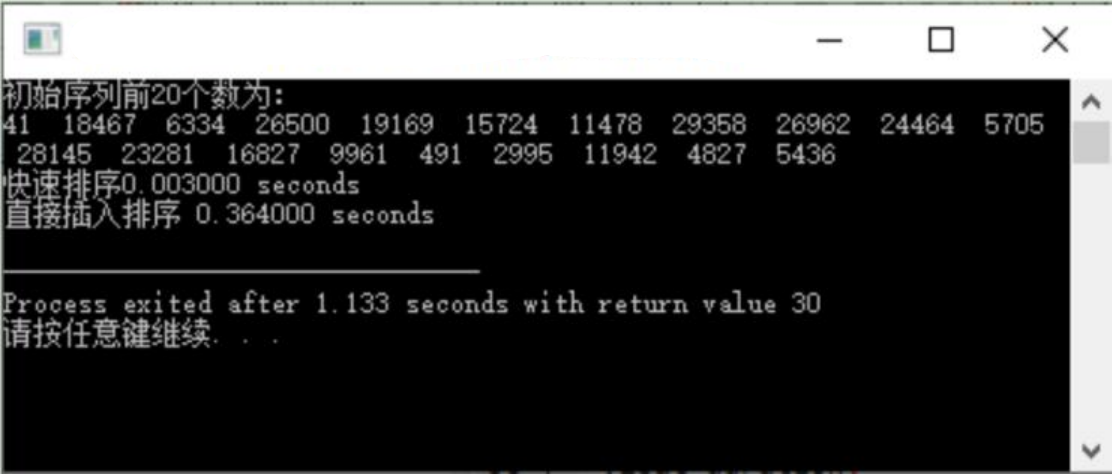
三、实验源代码

#include "stdio.h"
#include <iostream>
#include<cstring>
#include <stdlib.h>
#include <time.h>
using namespace std;int N = 10000; //随机数的个数//插入入排序
void insertSort(int arr[])
{int n = N;for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;// 将 key 插入到已排序的序列中while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}
}//希尔排序
void shellSort(int arr[]) {int n = N;int i, j, gap, temp;for (gap = n / 2; gap > 0; gap /= 2) {for (i = gap; i < n; i++) {temp = arr[i];for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}
}//快速排序
void quickSort(int s[], int l, int r)
{if (l < r){//Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1int i = l, j = r, x = s[l];while (i < j){while(i < j && s[j] >= x) // 从右向左找第一个小于x的数j--;  if(i < j) s[i++] = s[j];while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数i++;  if(i < j) s[j--] = s[i];}s[i] = x;quickSort(s, l, i - 1); // 递归调用 quickSort(s, i + 1, r);}
}//堆排序
void swap(int *a, int *b) {int temp = *b;*b = *a;*a = temp;
}void max_heapify(int arr[], int start, int end) {// 建立父節點指標和子節點指標int dad = start;int son = dad * 2 + 1;while (son <= end) { // 若子節點指標在範圍內才做比較if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的son++;if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數return;else { // 否則交換父子內容再繼續子節點和孫節點比較swap(&arr[dad], &arr[son]);dad = son;son = dad * 2 + 1;}}
}void heapSort(int arr[], int len) {int i;// 初始化，i從最後一個父節點開始調整for (i = len / 2 - 1; i >= 0; i--)max_heapify(arr, i, len - 1);// 先將第一個元素和已排好元素前一位做交換，再重新調整，直到排序完畢for (i = len - 1; i > 0; i--) {swap(&arr[0], &arr[i]);max_heapify(arr, 0, i - 1);}
}
//输出数组 a 的前20为元素，元素不足20个则输出全部
void print(int a[])
{int n =  N < 20 ? N : 20;for(int i=0;i<n;i++)cout << a[i] << " ";cout << endl;
}//产生随机数填充a数组
void init(int a[])
{for(int i=0;i<N;i++)a[i]=rand()%1000000;
}double getQuickSortTime(int a[])
{
//	cout << "排序前数组的前20位元素：\n";
//	print(a);clock_t first,second; //记录开始和结束时间(以毫秒为单位)first=clock(); //开始时间quickSort(a,0,N-1);second=clock();//结束时间
//	cout << "排序后数组的前20位元素：\n";
//	print(a);return (double)(second - first) / CLOCKS_PER_SEC;
}double getShellSortTime(int a[])
{clock_t first,second; //记录开始和结束时间(以毫秒为单位)
//	cout << "排序前数组的前20位元素：\n";
//	print(a);first=clock(); //开始时间shellSort(a);second=clock();//结束时间
//	cout << "排序后数组的前20位元素：\n";
//	print(a);return (double)(second - first) / CLOCKS_PER_SEC;
}double getHeapSortTime(int a[])
{clock_t first,second; //记录开始和结束时间(以毫秒为单位)
//	cout << "排序前数组的前20位元素：\n";
//	print(a);first=clock(); //开始时间heapSort(a,N);second=clock();//结束时间
//	cout << "排序后数组的前20位元素：\n";
//	print(a);return (double)(second - first) / CLOCKS_PER_SEC;
}void testSort()
{double quick = 0.0;double shell = 0.0;double heap = 0.0;int cnt = 10;//测试次数int a[N];//存放随机数for(int i = 0; i < cnt; i++){
//		if(i%5 == 0)
//			N *= 10;init(a);int t[N];memcpy(t,a,N);quick += getQuickSortTime(t);memcpy(t,a,N);shell += getShellSortTime(t);memcpy(t,a,N);heap += getHeapSortTime(t);}
//	cout.precision(5);cout.setf(ios::fixed);cout << "基于"<< N <<"个元素的随机数组进行排序，测试"<<cnt<<"次取平均值的结果如下：\n";cout << "快速排序：" << quick/cnt << "s\n";cout << "希尔排序：" << shell/cnt << "s\n";cout << " 堆排序 ：" << heap/cnt << "s\n";
}int main()
{ testSort();//	cout << "排序前数组的前20位元素：\n";
//	print(iN);
//	heapSort(iN,N);//显示排序算法所用的时间
//	cout << "排序后数组的前20位元素：\n";
//	cout <<"first: " << first << " second: " << second << endl; 
//	cout << "排序耗费的时间：";
//	cout <<  (double)(second - first) / CLOCKS_PER_SEC << "s" << endl;
}

四、实验结果

基于10000个元素的随机数组进行排序，测试10次取平均值的结果如下：
快速排序：0.008402s
希尔排序：0.001554s堆排序 ：0.001759s

五、实验总结

奇了怪了