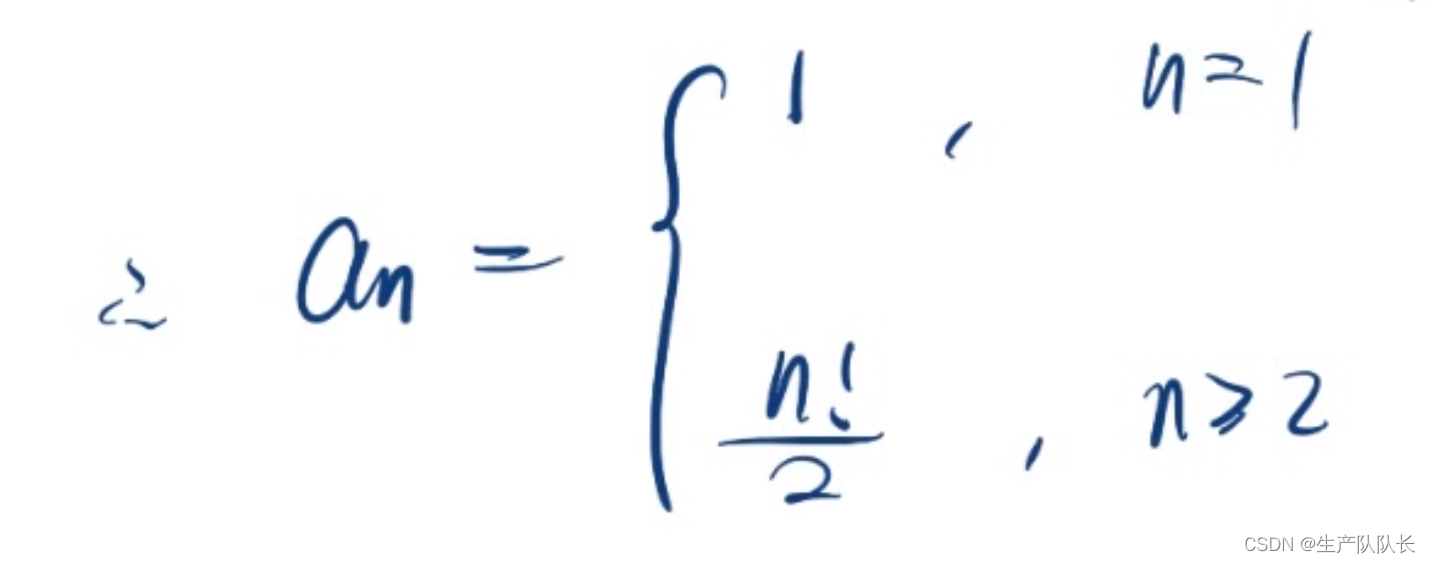相关文章
【高中数学/基本不等式】若正数a,b满足a>b,且1/(a+b)+1/(a-b)=1,则3a+2b的最小值是?
【问题】 若正数a,b满足a>b,且1/(a+b)+1/(a-b)=1,则3a+2b的最小值是? 【来源】 《解题卡壳怎么办 高中数学解题智慧点剖析》P38 余继光 苏德矿合著 浙江大学出版社出版 【如何破题】 1/(a+b)+1/(a-b)=1这个关系式挺复杂,展开后更乱(用三角函数也帮不上忙),而3a+2b这个表达式相对简单; 如果想让两者相乘,可以用配方的手段,得出的结果一部分能
【高中数学/极值/判别式法】已知实数a和b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是?
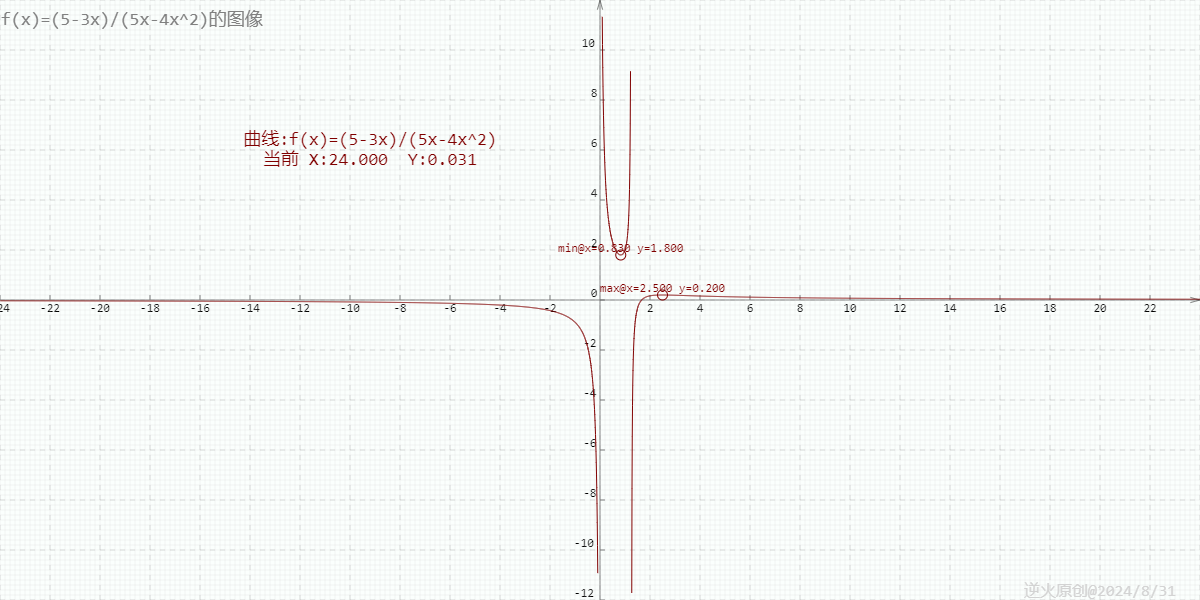
【问题】 已知实数a,b,b在(0,1)区间,a-b=1,则1/(a-1)+1/(5-4b)的最小值是? 【来源】 《解题卡壳怎么办 高中数学解题智慧点剖析》P34 余继光 苏德矿合著 浙江大学出版社出版 【破题点】 将a-1用b取代,发现结果是二次式相除,正好可用判别式法。 【解答】 由a-b=1得到a-1=b 于是原式=1/b+1/(5-4b) 设b为x,结果为y,得到表达式
gurobi约束条件使用大全(`model.addConstr()`添加单个约束和`model.addConstrs()`添加多个约束和强不等式约束)
文章目录 gurobi约束条件`model.addConstr()`添加单个约束`model.addConstrs()`添加多个约束强不等式约束 gurobi约束条件 model.addConstr()添加单个约束 约束可以是线性、不等式或等式。Gurobi支持添加单个约束和多重约束。 例子: model.addConstr(x + y == 5, "eq_const
高中数学:数列-累加法与累乘法
一、累加法 主要用来解决类似等差数列递推公式的相关变形题目 1、推导等差数列的通项公式 2、题型1 对递推式变形,通项的系数为1,常数项d变成含n的一次函数 解: 题型2 对递推式变形,通项的系数为1,常数项d变成含n的指数函数 解: 题型3 对题型2的变形 解: 二、累乘法 主要用来解决类似等比数列递推公式的相关变形题目 1、推导等比数列通项公式
概率的三条基本公理 | 布尔不等式的应用(举例)
概率论的三条基本公理由俄罗斯数学家柯尔莫哥洛夫(Andrey Kolmogorov)在1933年提出,被称为柯尔莫哥洛夫公理。它们构成了现代概率论的基础。这三条公理如下: 公理 1:非负性 公理 2:规范性 公理 3:可加性 布尔不等式 对于任意的事件集合 { A 1 , A 2 , … , A n } \{A_1, A_2, \ldots, A_n\} {A1,A2,…,An}
概率论与数理统计 -- 大数定理及切比雪夫不等式整理
大数定理、切比雪夫不等式及其推导 大数定律 弱大数定律(Weak Law of Large Numbers, WLLN) 弱大数定律指出,当试验次数 (n) 趋向无穷大时,样本平均值 (\bar{X_n}) 与期望值 (\mu) 之间的差异以概率收敛于0。数学上表示为: ∀ ϵ > 0 , lim n → ∞ P ( ∣ 1 n ∑ i = 1 n X i − μ ∣ ≥ ϵ ) =
算法数据结构(三十六)----四边形不等式技巧
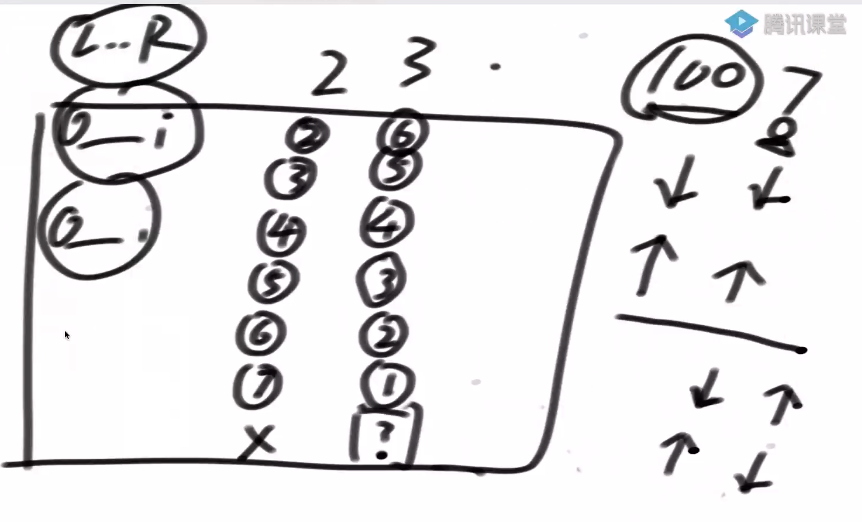
题目一 给定一个非负数组arr,长度为N, 那么有N-1种方案可以把arr切成左右两部分 每一种方案都有,min{左部分累加和,右部分累加和} 求这么多方案中,min{左部分累加和,右部分累加和}的最大值是多少? 整个过程要求时间复杂度O(N) //暴力求解public static int bestSplit1(int[] arr) {if (arr == null || arr.l
高中数学:数列-等差数列
一、概念 等差中项 二、通项公式 三、练习 例题1 例题2 an=a1+(n-1)d 等差数列求通式的问题,我们只要知道任意两项 利用二元一次方程组的思想,列出方程组 就可以求出通项公式。
高中数学:解三角形-大题练习(第二问解题方法整理)
一、题型归纳 1、最值问题 例题1、例题2 2、恒等变换 例题3、例题4、例题5、例题6 3、图形问题 例题7、例题8 例题1 解析 第二小问 首先,正弦定理和余弦定理都可以解决这一题。下面我给出两种解法 1、余弦定理+基本不等式 2、正弦定理+辅助角公式 例题2 解析 第二小问 这里求三角形面积,高中的面积公式是: S=½*ab*sinC S=½*ac*sinB
高中数学:解三角形-大题练习
例题1 解析 第一小问 根据条件等式,我们发现,每一项都含有边,但是,不是每一项都含有角 于是,我们要想到用正弦定理把边换为角来解答该题 第二小问 例题2 解析 第一小问 两个等式条件,各个项都含有边,也同时含有角,所以,可以把边化为角,也可以把角化为边 那么,如何选择了? 我们看到,这里要求的是cosB的值,所以,我们应该想到余弦定理 因此,我们应该把条件中的角换为边。 第二