本文主要是介绍高中数学:解三角形-大题练习(第二问解题方法整理),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、题型归纳
1、最值问题
例题1、例题2
2、恒等变换
例题3、例题4、例题5、例题6
3、图形问题
例题7、例题8
例题1

解析
第二小问
首先,正弦定理和余弦定理都可以解决这一题。下面我给出两种解法
1、余弦定理+基本不等式

2、正弦定理+辅助角公式

例题2

解析
第二小问
这里求三角形面积,高中的面积公式是:
S=½*ab*sinC
S=½*ac*sinB
S=½*bc*sinA
这一题给出了∠A,所以,我们选择第三个
于是S=½*bc*sinA=½*2c*sin60=(√3/2)*c
问题转化成了求c的范围
这里给出两种解法
1、根据正弦定理,将边的范围转化成角的范围求解
2、对于定角定边的问题,画图确定c的范围(推荐)
解法1

解法2
因为∠A是定值,边b是定值,所以,能变化的就是c的变成
又由于是锐角三角形,
所以,两个极限情况就是,∠B=90、∠C=90。求出这两个极限角度时c对应的长度即可。

例题3

解析
第二小问
首先展开待求式,在结合二倍角公式展开,即可得解
例题4

解析
第二小问
根据三角恒等变换展开,即可求出sinA和cosA的值。
从而利用正弦定理,得解
例题5

解析
第二小问
由于,第一小问,已经求出∠A=60,且没有给出边a的值,所以,这一题选用正弦定理求解
将待求式中的边化为角,然后,进行三角函数的恒等变化,从而得解。
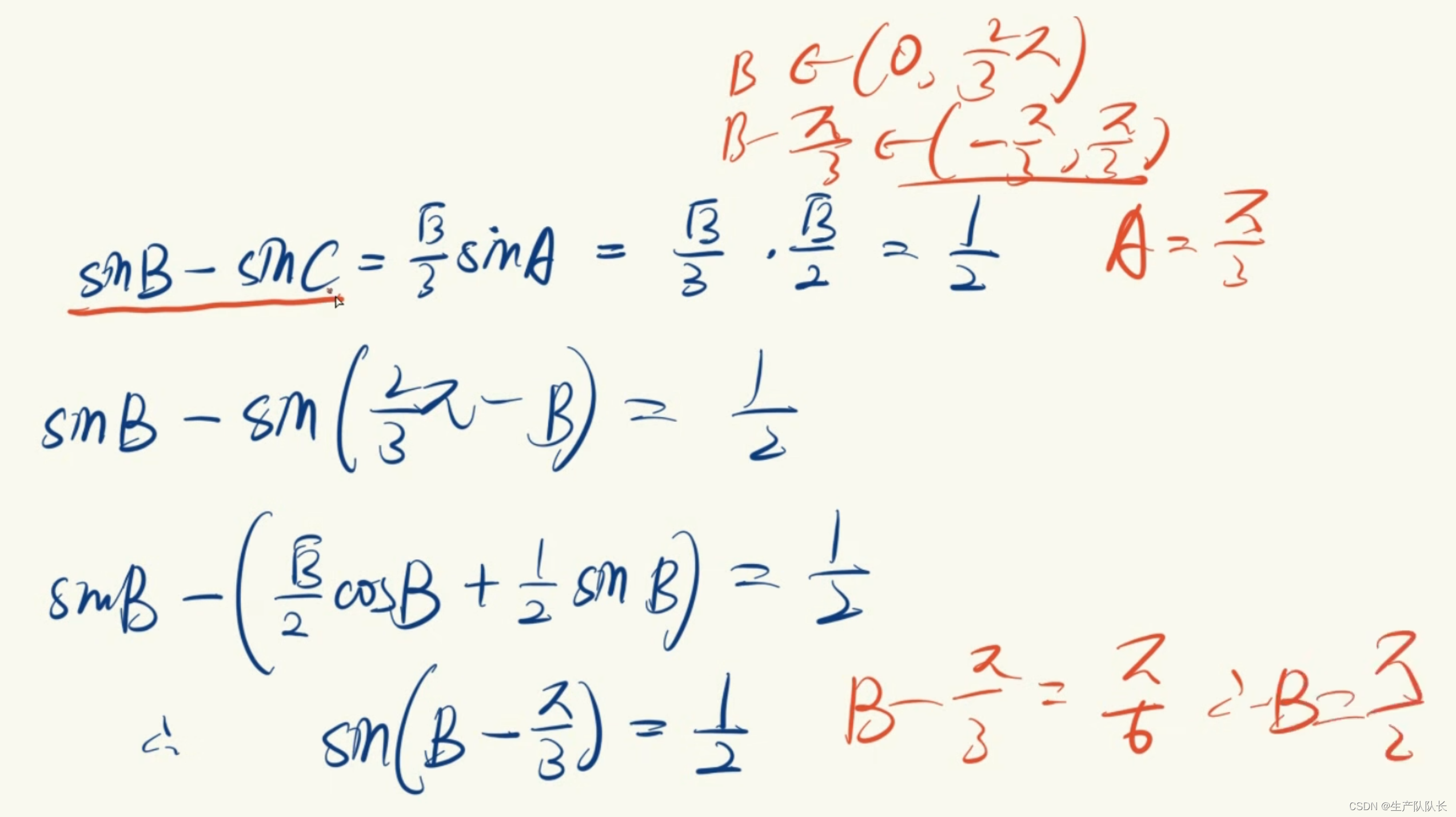
例题6

解析
第二小问
这里求的是a+c,我可以想到平方后的展开式中含有a^2+b^2
所以,联想到cosB的余弦定理。
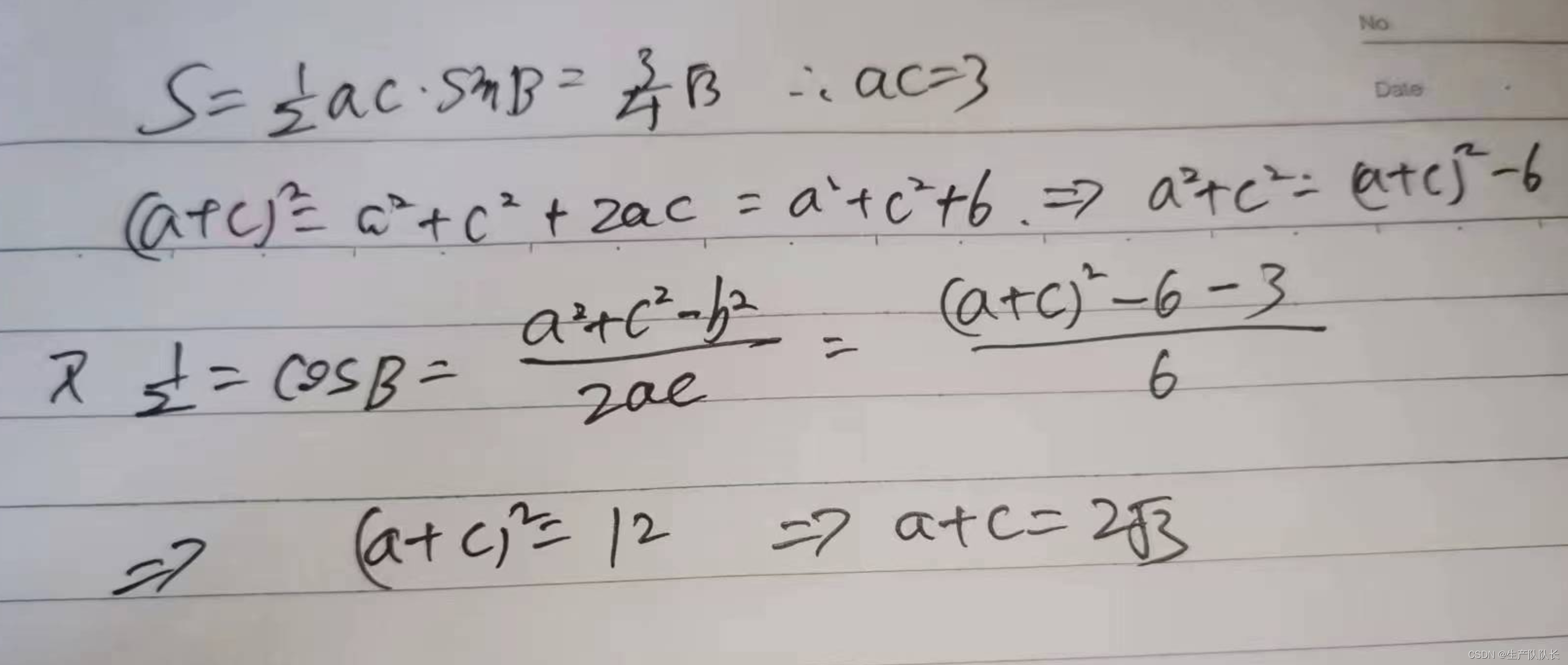
例题7

解析
第一小问
给出了ac边和B的角度,所以,可以用∠B的余弦定理求出边b的长度
再用正弦定理,求出sinC的值
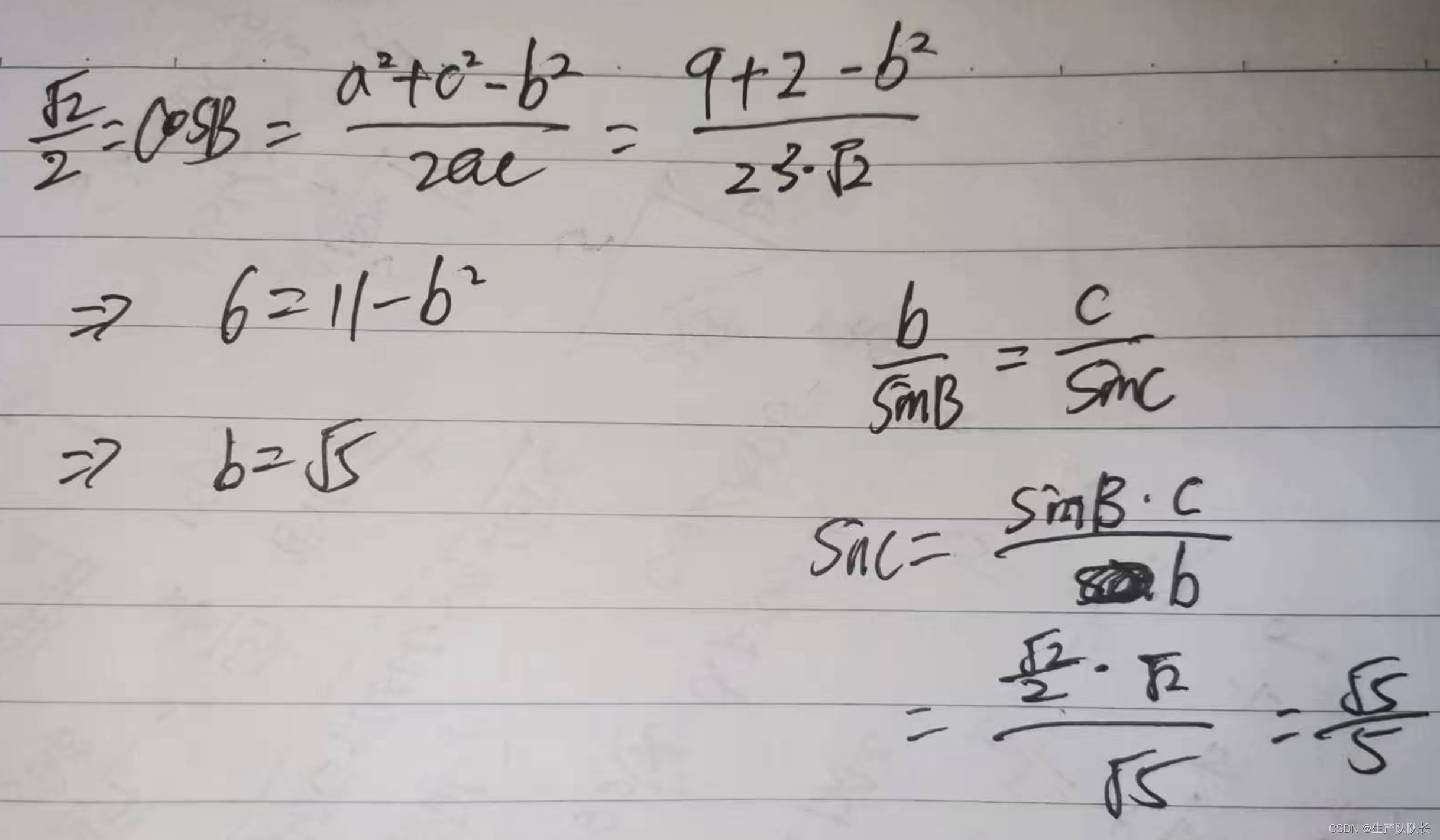
第二小问

例题8
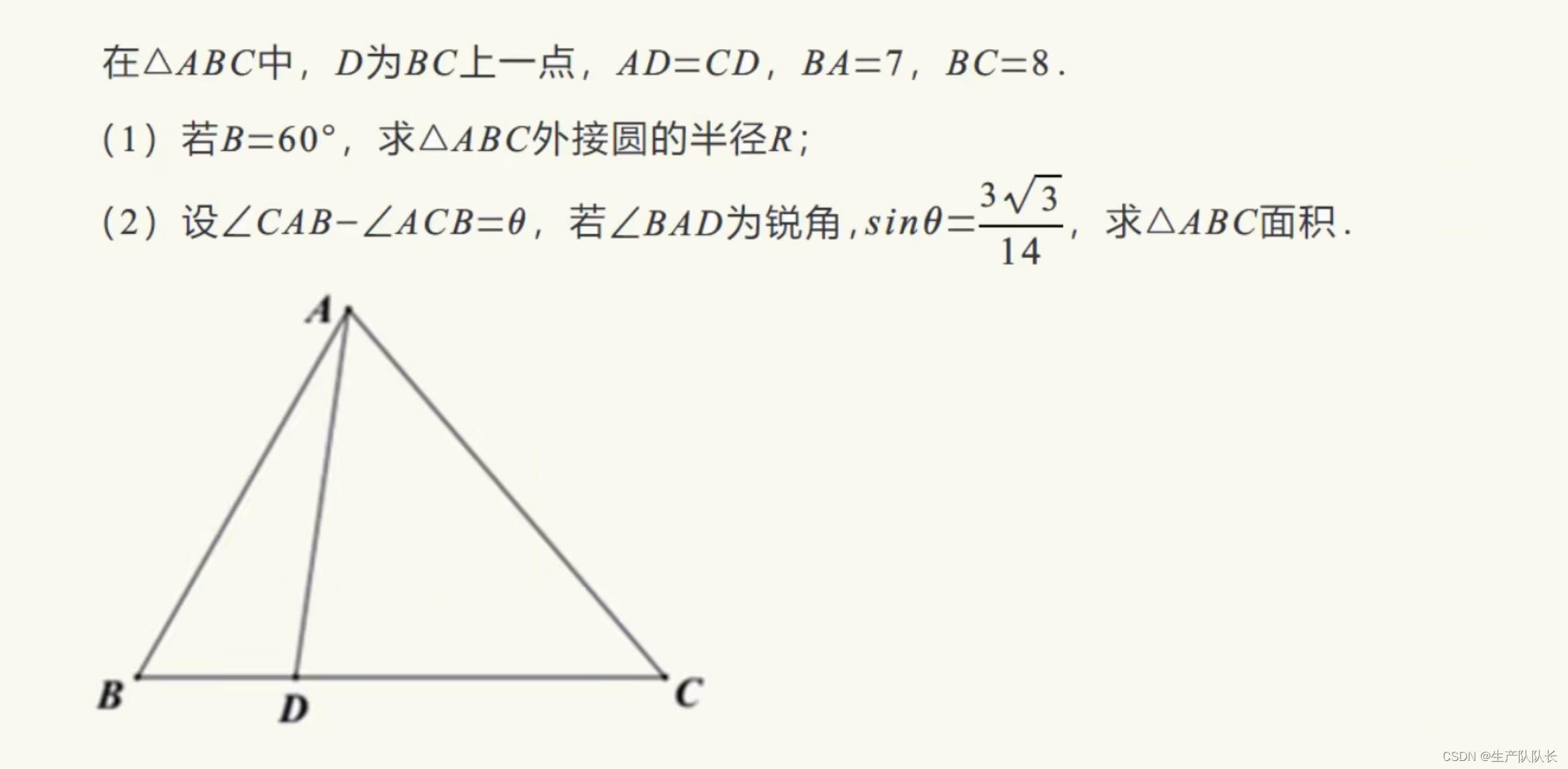
解析
第一小问
条件给出了两边及其夹角,直接考虑用余弦定理,求出第三边长度
在根据正弦定理求出外接圆半径r即可。
如果给出两边及邻角,则考虑用正弦定理求出另外一角,在结合三角恒定变换,求出第三边。

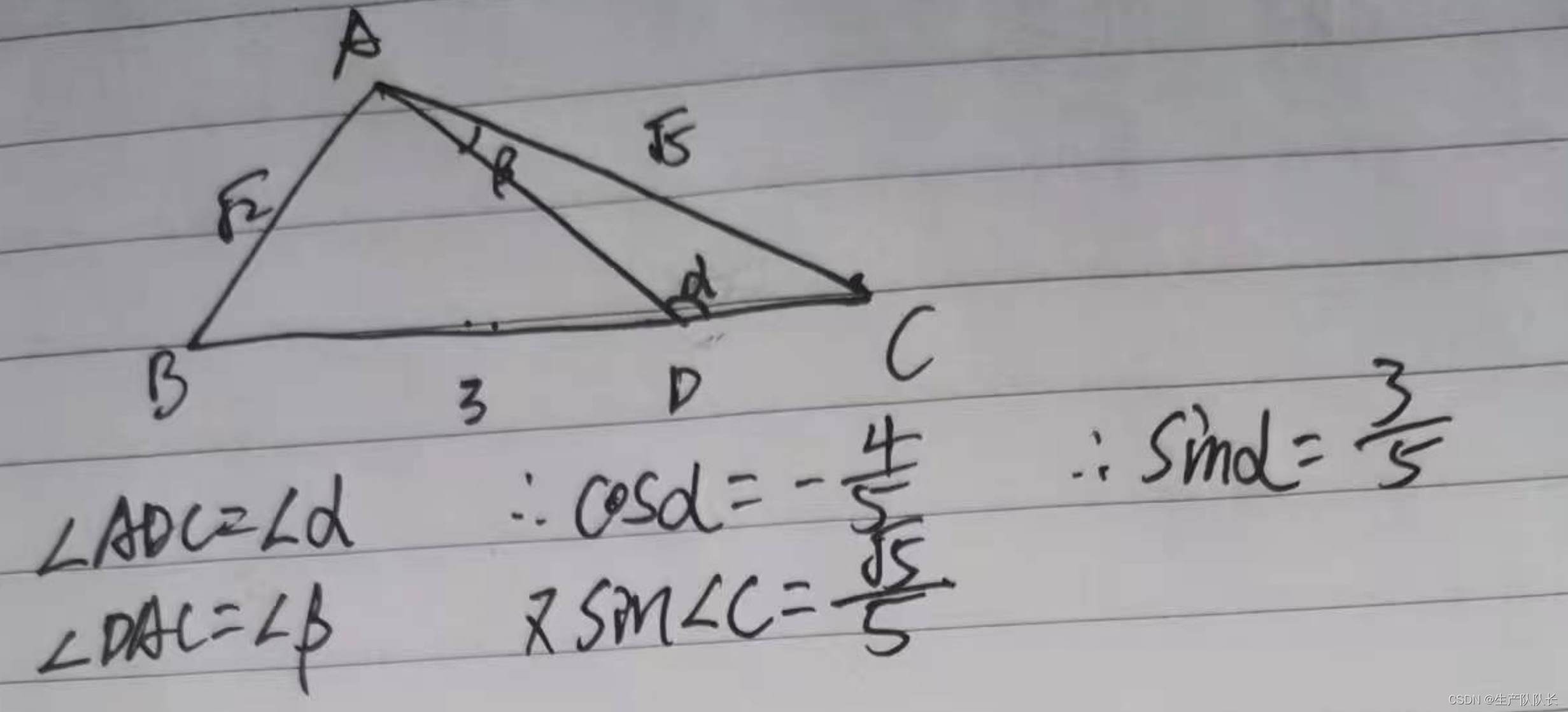
第二小问
首先根据条件,找出AD与BD之间的数量关系,在根据余弦定理,求出各边长。
在根据正弦定理,求出sinα,得解。

这篇关于高中数学:解三角形-大题练习(第二问解题方法整理)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



