本文主要是介绍决策树中的熵、条件熵、信息增益和Gini指数计算示例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 信息
- 熵
- 条件熵
- 信息增益
- 公式
- 计算
- Gini指数
- 计算示例
信息
首先我们从什么是信息来着手分析:
I ( X = x i ) = − l o g 2 p ( x i ) I_{(X = x_i)} = -log_2p(x_i) I(X=xi)=−log2p(xi)
I ( x ) I(x) I(x)用来表示随机变量的信息, p ( x i ) p(x_i) p(xi)指是当 x i xi xi发生时的概率。
熵
在信息论和概率论中熵是对随机变量不确定性的度量,与上边联系起来,熵便是信息的期望值:
H ( D ) = ∑ i = 1 n p ( x i ) I ( x i ) = − ∑ i = 1 n p ( x i ) l o g 2 p ( x i ) H_{(D)}=\sum_{i=1}^np(x_i)I(x_i) = -\sum_{i=1}^np(x_i)log_2p(x_i) H(D)=∑i=1np(xi)I(xi)=−∑i=1np(xi)log2p(xi)
x i x_i xi表示第 i i i类。
熵只依赖X的分布,和X的取值没有关系,熵是用来度量不确定性,当熵越大,概率说X=xi的不确定性越大,反之越小,在机器学期中分类中说,熵越大即这个类别的不确定性更大,反之越小,当随机变量的取值为两个时,熵随概率的变化曲线如下图:
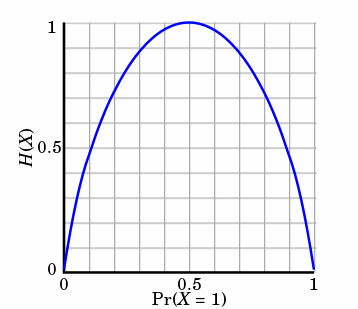
当p=0或p=1时,H§=0,随机变量完全没有不确定性,当p=0.5时,H§=1,此时随机变量的不确定性最大
条件熵
条件熵是用来解释信息增益而引入的概念,概率定义:随机变量X在给定条件下随机变量Y的条件熵,对定义描述为:X给定条件下Y的条件概率分布的熵对X的数学期望,在机器学习中为选定某个特征后的熵,公式如下:
H ( Y ∣ X ) = ∑ x p ( x ) H ( Y ∣ X = x ) H_{(Y|X)} = \sum_xp(x)H_{(Y|X=x)} H(Y∣X)=∑xp(x)H(Y∣X=x)
这里可能会有疑惑,这个公式是对条件概率熵求期望,但是上边说是选定某个特征的熵,没错,是选定某个特征的熵,因为一个特征可以将待分类的事物集合分为多类,即一个特征对应着多个类别,因此在此的多个分类即为X的取值。
信息增益
公式
信息增益在决策树算法中是用来选择特征的指标,信息增益越大,则这个特征的选择性越好,在概率中定义为:待分类的集合的熵和选定某个特征的条件熵之差(这里只的是经验熵或经验条件熵,由于真正的熵并不知道,是根据样本计算出来的),公式如下:
I G ( Y ∣ X ) = H ( Y ) − H ( Y ∣ X ) IG_{(Y|X)} = H_{(Y)}- H_{(Y|X)} IG(Y∣X)=H(Y)−H(Y∣X)
注意:这里不要理解偏差,因为上边说了熵是类别的,但是在这里又说是集合的熵,没区别,因为在计算熵的时候是根据各个类别对应的值求期望来等到熵。
计算
训练数据集合D,|D|为样本容量,即样本的个数(D中元素个数),设有K个类Ck来表示,|Ck|为Ci的样本个数,|Ck|之和为|D|,k=1,2…,根据特征A将D划分为n个子集D1,D2…Dn,|Di|为Di的样本个数,|Di|之和为|D|,i=1,2,…,记Di中属于Ck的样本集合为Dik,即交集,|Dik|为Dik的样本个数,算法如下:
输入:D,A
输出:信息增益g(D,A)
-
D的经验熵 H ( D ) H_{(D)} H(D): H ( D ) = − ∑ k = 1 K C k D l o g 2 C k D H_{(D)} = -\sum_{k=1}^K\frac{C_k}{D}log_2\frac{C_k}{D} H(D)=−∑k=1KDCklog2DCk
此处的概率计算是根据古典概率计算,由于训练数据集总个数为|D|,某个分类的个数为|Ck|,在某个分类的概率,或说随机变量取某值的概率为:|Ck|/|D|
. 选定A的经验条件熵 H ( D / A ) H_{(D/A)} H(D/A) H ( D / A ) = ∑ i = 1 n D i D H ( D i ) H_{(D/A)} = \sum_{i=1}^n\frac{D_i}{D}H_{(D_i)} H(D/A)=∑i=1nDDiH(Di) = − ∑ i = 1 n D i D ∑ k = 1 K D i k D i l o g 2 D i k D i -\sum_{i=1}^n\frac{D_i}{D}\sum_{k=1}^K\frac{D_{ik}}{D_i}log_2\frac{D_{ik}}{D_i} −∑i=1nDDi∑k=1KDiDiklog2DiDik
此处的概率计算同上,由于|Di|是选定特征的某个分类的样本个数,则|Di|/|D|,可以说为在选定特征某个分类的概率,后边的求和可以理解为在选定特征的某个类别下的条件概率的熵,即训练集为Di,交集Dik可以理解在Di条件下某个分类的样本个数,即k为某个分类,就是缩小训练集为Di的熵
-
信息增益: g ( D , A ) = H ( D ) − H ( D ∣ A ) g_{(D,A)} = H_{(D)} - H_{(D|A)} g(D,A)=H(D)−H(D∣A)
Gini指数
定义:假设有K个类,样本点属于第k类的概率为 p k p_k pk
公式:
G i n i ( p ) = ∑ k = 1 K p k ∗ ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p) = \sum_{k=1}^K{{p_k}*(1-p_k)} = 1 - \sum_{k=1}^K{p_k}^2 Gini(p)=∑k=1Kpk∗(1−pk)=1−∑k=1Kpk2
对于数据集D:
G i n i ( D ) = 1 − ∑ k = 1 K ( C k D ) 2 Gini(D) = 1 - \sum_{k=1}^K(\frac{C_k}{D})^2 Gini(D)=1−∑k=1K(DCk)2
对于特征A将D划分成 D 1 D_1 D1和 D 2 D_2 D2,则
G i n i ( D , A ) = D 1 D G i n i ( D 1 ) + D 2 D G i n i ( D 2 ) Gini_{(D,A)} = \frac{D1}{D}Gini(D_1)+\frac{D_2}{D}Gini(D_2) Gini(D,A)=DD1Gini(D1)+DD2Gini(D2)
- Gini最小为0,此时表示所有样本都被分到了一类,效果最好。
- Gini最大时, p k p_k pk都是0.5,效果最差
计算示例
| 名称 | 是否用鳃呼吸 | 有无鱼鳍 | 是否为鱼 |
|---|---|---|---|
| 鲨鱼 | 1 | 1 | 1 |
| 鲫鱼 | 1 | 1 | 1 |
| 河蚌 | 1 | 0 | 0 |
| 鲸 | 0 | 1 | 0 |
| 海豚 | 0 | 1 | 0 |
-
熵
H ( D ) = − ∑ i = 1 n p ( x i ) l o g 2 p ( x i ) H_{(D)} = -\sum_{i=1}^np(x_i)log_2p(x_i) H(D)=−∑i=1np(xi)log2p(xi)
= − ( 2 5 l o g 2 5 + 3 5 l o g 3 5 ) = -(\frac{2}{5}log\frac{2}{5}+\frac{3}{5}log\frac{3}{5}) =−(52log52+53log53)
= 0.971 =0.971 =0.971
当样本按照特征A的值a划分成两个独立的子数据 集 D 1 集D1 集D1和 D 2 D2 D2时,此时整个数据集D的熵分为两个独立数据集 D 1 D1 D1的熵和 D 2 D2 D2的熵的加权和,即:
H ( D ) = D 1 D H ( D 1 ) + D 2 D H ( D 2 ) H_{(D)} = \frac{D_1}{D}H_{(D_1)}+\frac{D_2}{D}H_{(D_2)} H(D)=DD1H(D1)+DD2H(D2)
若特征A为“是否用鳃呼吸”划分数据,则数据D的信息熵为:
H ( D ) = 3 5 H ( D 1 ) + 2 5 H ( D 2 ) H_{(D)} = \frac{3}{5}H_{(D_1)}+\frac{2}{5}H_{(D_2)} H(D)=53H(D1)+52H(D2)
= − [ 3 5 ( 2 3 l o g 2 3 + 1 3 l o g 1 3 ) + 2 5 ( 1 l o g 1 ) ] = -[\frac{3}{5}(\frac{2}{3}log\frac{2}{3}+\frac{1}{3}log\frac{1}{3})+\frac{2}{5}(1log1)] =−[53(32log32+31log31)+52(1log1)]
= 0.551 = 0.551 =0.551
-
信息增益
由上述的划分可以看出,在划分后的数据集D的信息熵减小了,对于给定的数据集,划分前后信息熵的减少量称为信息增益(information gain),即:
I G ( D , A ) = H ( D ) − ∑ p = 1 P D p D H ( D p ) IG_{(D,A)} = H_{(D)} - \sum_{p=1}^P\frac{D_p}{D}H_{(D_p)} IG(D,A)=H(D)−∑p=1PDDpH(Dp)
$ = 0.971−0.551$
$ = 0.44 $ -
信息增益率
I G r ( D , A ) = I G ( D , A ) H A ( D ) IGr_{(D,A)} = \frac{IG_{(D,A)}}{H_A(D)} IGr(D,A)=HA(D)IG(D,A)
其中 H A ( D ) H_A(D) HA(D)为,对于样本集合D将特征A作为随机变量(取值是特征A的各个特征值),求得的经验熵。
H A ( D ) = − ∑ i = 1 n D i D l o g D i D H_A(D) = -\sum_{i=1}^n\frac{D_i}{D}log\frac{D_i}{D} HA(D)=−i=1∑nDDilogDDi
= − [ 3 5 l o g 3 5 + 2 5 l o g 2 5 ] = 0.971 = -[\frac{3}{5}log\frac{3}{5}+\frac{2}{5}log\frac{2}{5}] = 0.971 =−[53log53+52log52]=0.971
I G r ( D , A ) = 0.44 0.971 = 0.453 IGr_{(D,A)} = \frac{0.44}{0.971} = 0.453 IGr(D,A)=0.9710.44=0.453
-
Gini指数
对于数据集D G i n i ( D ) = 1 − [ ( 2 5 ) 2 + ( 3 5 ) 2 ] Gini_{(D)} = 1 - [(\frac{2}{5})^2+(\frac{3}{5})^2] Gini(D)=1−[(52)2+(53)2]
特征A划分后 G i n i ( D , A ) = 3 5 ∗ [ 1 − [ ( 2 3 ) 2 + ( 1 3 ) 2 ] ] + 2 5 ∗ [ 1 − 1 2 ] = 0.627 Gini_{(D,A)} = \frac{3}{5}*[1-[(\frac{2}{3})^2+(\frac{1}{3})^2]] +\frac{2}{5}*[1-1^2] = 0.627 Gini(D,A)=53∗[1−[(32)2+(31)2]]+52∗[1−12]=0.627
这篇关于决策树中的熵、条件熵、信息增益和Gini指数计算示例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




