算法策略 - 贪心（Greedy）

本文主要是介绍算法策略 - 贪心（Greedy），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

• 贪心策略，也称贪婪策略
• 每一步都采取当前状态下最优的选择（局部最优解），从而希望推导出全局最优解
• 贪心应用：

1. 哈夫曼树
2. 最小生成树算法：Prim、Kruskal
3. 最短路径算法：Dijkstra

练习1 - 最优装载问题（加勒比海盗）

在北美洲东南部，有一片神秘的海域，是海盗最活跃的加勒比海盗
有一天，海盗们截获了一艘装满各种各样古董的货船，每一件古董都价值连城，一单打碎就失去了它的价值
海盗船的载重量为W，每件古董的重量为w，海盗们该如何把尽可能多数量的古董装上海盗船？
比如W为30，w分别为3、5、4、10、7、14、2、11

• 贪心策略：每一次都优先选择重量最小的古董

1. 选择重量为2的古董，剩重量28
2. 选择重量为3的古董，剩重量25
3. 选择重量为4的古董，剩重量21
4. 选择重量为5的古董，剩重量16
5. 选择重量为7的古董，剩重量9

• 最多能装载5个古董

int capacity = 30
int[] weights = {3, 5, 4, 10, 7, 14, 2, 11};
int count = 0, weight = 0;
Arrays.sort(weights);
for (int i = 0; i < weights.length && weight < capacity; i++) {int newWeight = weight +weights[i];if (newWeight <= capacity) {weight = newWeight;count++;}
}

练习2 - 零钱兑换

假设有25分、10分、5分、1分的硬币，现要找给客户41分的零钱，如何办到硬币个数最少？

• 贪心策略：每次都优先选择面值最大的硬币

1. 选择25分的硬币，剩16分
2. 选择10分的硬币，剩6分
3. 选择5分的硬币，剩1分
4. 选择1分的硬币

• 最终的解是共4枚硬币

Integer[] faces = {25, 10, 5, 1};
Arrays.sort(faces);
int coins = 0, money = 41;
int idx = faces.length - 1;
while (idx >= 0) {while (money >= faces[idx]) {money -= faces[idx];coins++;}idx--;
}

零钱兑换的另一个例子

假设有25分、20分、5分、1分的硬币，现要找给客户41分的零钱，如何办到硬币个数最少？

• 贪心策略：每一步都优先选择面值最大的硬币

1. 选择25分的硬币，剩16分
2. 选择5分的硬币，剩11分
3. 选择5分的硬币，剩6分
4. 选择5分的硬币，剩1分
5. 选择1分的硬币

• 最终的解释1枚25分、3枚5分、1枚1分的硬币，共5枚硬币
• 实际上本体的最优解是：2枚20分、1枚1分的硬币，共3枚硬币

注意

• 贪心策略并不一定能得到全局最优解
• 因为一般没有测试所有可能的解，容易过早做决定，所以没法达到最佳解
• 贪图眼前局部的利益最大化，看不到长远未来，走一步看一步
• 优点：简单、高效、不需要穷举所有可能，通常作为其他算法的辅助算法来使用
• 缺点：鼠目寸光，不从整体上考虑其他可能，每次采取局部最优解，不会再回溯，因此很少情况会得到最优解

练习3 - 0-1背包

有n件物品和一个最大承重为W的背包，没见物品的重量是w、价值是v
在保证总重量不超过W的前提下，将哪件物品装入背包，可以使得背包的总价值最大？
注意：每个物品只有1件，也就是每个物品只能选择0件或者1件，因此称为0-1背包问题

• 如果采取贪心策略，有3个方案

1. 价值主导：优先选择价值最高的物品放进背包
2. 重量主导：优先选择重量最轻的物品放进背包
3. 价值密度主导：优先选择价值密度最高的物品放进背包（价值密度 = 价值 / 重量）

0-1背包 - 实例

• 假设背包最大承量150，7个物品如表哥所示
  

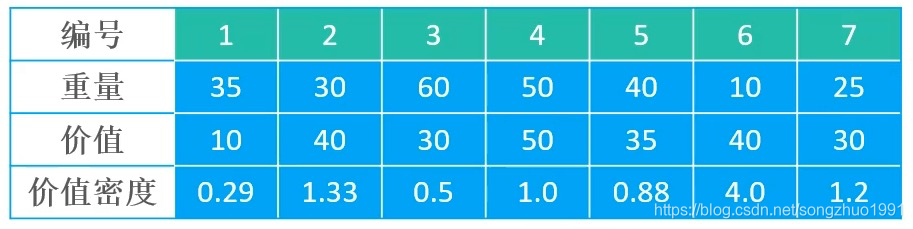
1. 价值主导：放入背包的物品编号是4、2、6、5，总重量130，总价值165
2. 重量主导：放入背包的物品编号是6、7、2、1、5，总重量140，总价值155
3. 价值密度主导：放入背包的物品编号是6、2、7、4、1，总重量150，总价值170

0-1背包 - 实现

void run(String title, Comparator<Article>comparator) {Article[] articles = new Article[] {new Article(35, 10), new Article(30, 40),new Article(60, 30), new Article(50, 50),new Article(40, 35), new Article(10, 40),new Article(25, 30)  };Arrays.sort(articles, comparator);int capacity = 150, weight = 0, value = 0;List<Article> selectedArticles = new ArrayList<>();for (int i = 0; i < articles.length && weight < capacity; i++) {int newWeight = articles[i].weight + weight;if (newWeight <= capacity) {selectedArticles.add(articles[i]);weight = newWeight;value += articles[i].value;}}System.out.println("-----------" + title + "-----------");System.out.println("总价值：" + value);for (Article article : selectedArticles) {System.out.println(article);}
}

run("重量主导", (Article a1, Article a2) -> {return a1.weight - a2.weight;
});
run("价值主导", (Article a1, Article a2) -> {return a2.value - a1.value;
});
run("价值密度主导", (Article a1, Article a2) -> {return Double.compare(a2.valueDensity, a1.valueDensity);
});

public class Article {int weight;int value;double valueDensity;public Article(int weight, int value) {this.weight = weight;this.value = value;valueDensity = value * 1.0 / weight;}@Overridepublic String toString() {return "[weight=" + weight +", value=" + value + "]";}
}

----------重量主导-----------
总价值：155
[weight=10, value=40]
[weight=25, value=30]
[weight=30, value=40]
[weight=35, value=10]
[weight=40, value=35]
----------价值主导-----------
总价值：165
[weight=50, value=50]
[weight=30, value=40]
[weight=10, value=40]
[weight=40, value=35]
----------价值密度主导-----------
总价值：170
[weight=10, value=40]
[weight=30, value=40]
[weight=25, value=30]
[weight=50, value=50]
[weight=35, value=10]

---

练习题：

• LeetCode — 455. 分发饼干

• LeetCode — 452. 用最少的数量的箭引爆气球

• LeetCode — 122. 买卖股票的最佳时机II

• LeetCode — 605. 种花问题

• LeetCode — 135. 分发糖果

这篇关于算法策略 - 贪心（Greedy）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---