标签传播算法(Label Propagation Algorithm)

目录：
1. 半监督学习(Semi-supervised Learning SSL)
2. 完全图
3. 标签传播算法的基本思路
4. 标签传播算法
5. 算法描述
6. 标签传播算法的基本特点
7. 代码实现

1. 半监督学习(Semi-supervised Learning SSL)

半监督学习是一种有监督学习和无监督学习想结合的一种方法，其主要思想是基于数据分布上的模型假设，利用少量的已标注数据进行指导并预测未标记数据的标记，并合并到标记数据集中去。

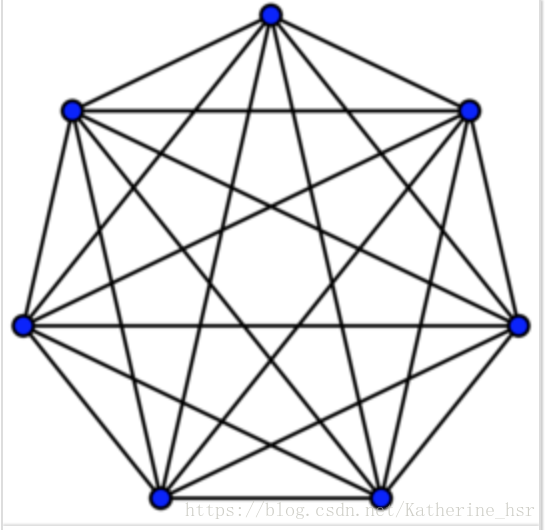
2. 完全图

在图论的数学领域，完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。完整的有向图又是一个有向图，其中每对不同的顶点通过一对唯一的边缘（每个方向一个）连接。n个端点的完全图有n个端点以及n(n − 1) / 2条边，以Kn表示。它是(k − 1)-正则图。所有完全图都是它本身的团（clique）

3. 标签传播算法的基本思路

标签传播算法是基于图的半监督学习方法，基本思路是从已标记的节点的标签信息来预测未标记的节点的标签信息，利用样本间的关系，建立完全图模型。
每个节点标签按相似度传播给相邻节点，在节点传播的每一步，每个节点根据相邻节点的标签来更新自己的标签，与该节点相似度越大，其相邻节点对其标注的影响权值越大，相似节点的标签越趋于一致，其标签就越容易传播。在标签传播过程中，保持已标记的数据的标签不变，使其将标签传给未标注的数据。最终当迭代结束时，相似节点的概率分布趋于相似，可以划分到一类中。

4.标签传播算法

1. 令 ( x 1 , y 1 ) . . . ( x l , y l ) 是 已 标 注 的 数 据 ， Y L = { y 1 , . . . y L } ∈ { 1 , . . . , C } (x_1, y_1)...(x_l, y_l)是已标注的数据，Y_L=\lbrace y_1, ... y_L \rbrace\in \lbrace1, ..., C\rbrace (x1​,y1​)...(xl​,yl​)是已标注的数据，YL​={y1​,...yL​}∈{1,...,C},类别数C已知，且均存在于标签数据中。令 ( x l + 1 , y l + 1 ) . . . ( x l + u , y l + u ) 为 未 标 注 数 据 ， 则 Y U = { y l + 1 , . . . , y l + u } 是 没 有 标 签 的 ， 通 常 l < < u ， 也 就 是 说 有 标 签 的 数 据 的 数 量 远 远 小 于 没 有 标 签 的 数 据 的 数 量 ， 让 X = { x 1 , . . , x l + u } ∈ R D , 则 问 题 转 换 为 从 X 和 Y L 中 去 预 测 Y U (x_{l+1},y_{l+1})...(x_{l+u}, y_{l+u})为未标注数据，则Y_U=\lbrace y_{l+1}, ..., y_{l+u} \rbrace 是没有标签的， 通常l<<u，也就是说有标签的数据的数量远远小于没有标签的数据的数量，让X= \lbrace{x_1, .., x_{l+u}} \rbrace\in R^D,则问题转换为从X和Y_L中去预测Y_U (xl+1​,yl+1​)...(xl+u​,yl+u​)为未标注数据，则YU​={yl+1​,...,